已知二次型经过正交变换化为标准型，求参数a,b及所用的正交变换矩阵

第1题：

求一个正交变换将二次型化成标准形

答案：

解析：

第2题：

已知二次型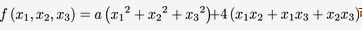可用正交变换化为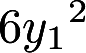.求a,并且作实现此转化的正交变换

答案：

解析：

第3题：

已知二次型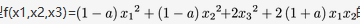的秩为2.(1)求a.(2)求作正交变换X=QY,把f(x1,x2,x3)化为标准形.(3)求方程f(x1,x2,x3)=0的解

答案：

解析：

第4题：

设二次型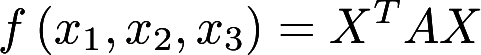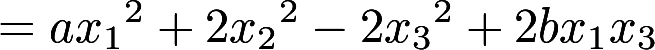,(b>0)其中A的特征值之和为1, 特征值之积为-12.(1) 求a,b. (2) 用正交变换化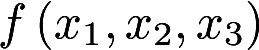为标准型

答案：

解析：

第5题：

设二次型f(x1,x2,x3)=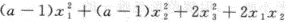（a>0）的秩为2.(1)求a;(2)用正交变换法化二次型为标准形.

答案：

解析：

第6题：

求正交变换，把二次曲面方程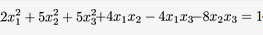化成标准方程

答案：

解析：

第7题：

已知a是常数，且矩阵可经初等列变换化为矩阵.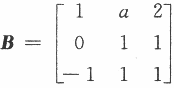
　　(Ⅰ)求a；
　　(Ⅱ)求满足AP=B的可逆矩阵P.

答案：

解析：

第8题：

设A为三阶实对称矩阵，如果二次曲面方程
　　
　　在正交变换下的标准方程的图形如图所示，
　　
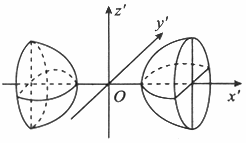
　　则A的正特征值的个数为

A.A0
B.1
C.2
D.3

答案：B

解析：

本题把线性代数与解析几何的内容有机的联系起来，首先要明白所给图形是什么曲面？其标准方程是什么？　　双叶双曲面，标准方程是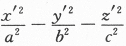：=1其次，二次型经正交变换化为标准形时，其平方项的系数就是A的特征值，所以应选(B).
很多考生选择(C)，是不是把标准方程记成了图1}　而忽略了本题的条件是x^TAx=1.

第9题：

三阶矩阵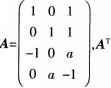 为矩阵A的转置，已知r(ATA)=2，且二次型
(1)求a；
(2)求二次型对应的二次矩阵，并将二次型化为标准型，写出正交变换过程。

答案：

解析：

(1)由r(ATA)=r(A)=2可得， (2）

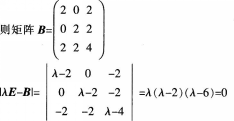
第10题：

空间坐标变换中的正交变换矩阵的（）个元素中只有（）个独立元素。

第11题：

简述正交变换的特点。

第12题：

第13题：

用配方法把二次型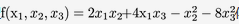化为标准型，并求所作变换

答案：

解析：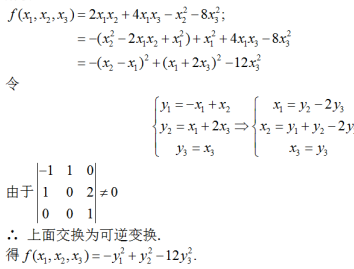

第14题：

设二次型
　　(b>0),
　　其中二次型的矩阵A的特征值之和为1，特征值之积为-12.
　　(1)求a，b的值；
　　(2)利用正交变换将二次型f化为标准形，并写出所用的正交变换和对应的正交矩阵.

答案：

解析：

第15题：

求一个正交变换把二次曲面的方程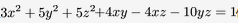化成标准方程

答案：

解析：

第16题：

设二次型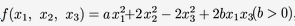其中二次型矩阵A的特征值之和为1, 特征值之积-12.(1) 求a,b的值; (2) 求一正交变换把二次型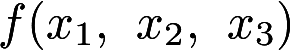化成标准型(需写出正交变换及标准型)

答案：

解析：

第17题：

已知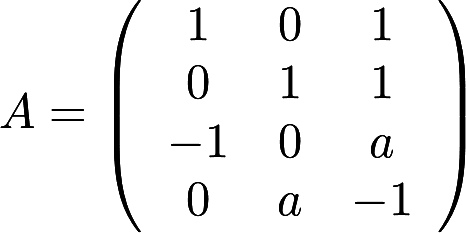，二次型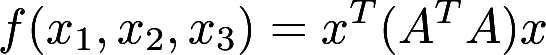的秩为2. （Ⅰ）求实数a的值； （Ⅱ）求正交变换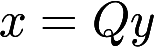将二次型化为标准型

答案：

解析：

第18题：

若二次曲面的方程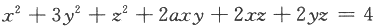经正交变换化为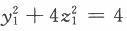，则a=________.

答案：1、1

解析：

本题又是一道线性代数与二次曲面的简单综合题.由于二次型xAx经正交变换化为标准形时，矩阵A的特征值就是标准形中平方项的系数，按题意，矩阵A的特征值是0，1，4，据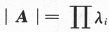，即
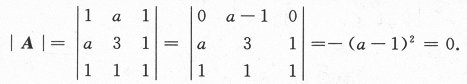　　可见a=1

第19题：

已知二次型f(x1，x2，3x)=x^TAx在正交变换x=Qy下的标准形为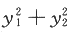，且Q的第3列为.
　　(Ⅰ)求矩阵A；
　　(Ⅱ)证明A+E为正定矩阵，其中E为三阶单位矩阵.

答案：

解析：

第20题：

设二次型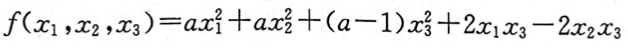的正惯性指数p=2,负惯性指数q=0,且可用可逆线性变换x=Cy将其化为二次型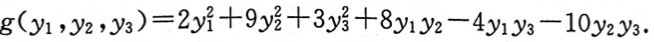（1）求常数a; (2）求可逆线性变换矩阵C

答案：

解析：

第21题：

设二次型f(x1,x2,x3)在正交变换为x=py下的标准形为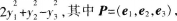
若Q=(e1-e3，e2)，则f(x1,x2,x3)在正交变换x=Qy下的标准型为( )。
A．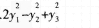
B．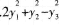
C．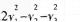
D．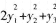

答案：A

解析：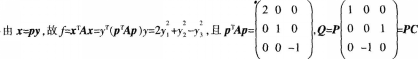

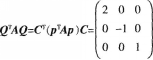
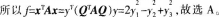
第22题：

什么是正交变换？用于图像处理的正交变换有哪些？各有何作用？。

第23题：