对最优化问题,若目标函数和约束很复杂,难以精确地求出其最优解时,则解决方式包括()。A.求近似最优解B.求精确的最优解C.求解几步的值作为解答D.随机获得值作为解答
题目
对最优化问题,若目标函数和约束很复杂,难以精确地求出其最优解时,则解决方式包括()。
A.求近似最优解
B.求精确的最优解
C.求解几步的值作为解答
D.随机获得值作为解答
相似考题
参考答案和解析
更多“对最优化问题,若目标函数和约束很复杂,难以精确地求出其最优解时,则解决方式包括()。”相关问题
-
第1题:
外点惩罚函数法将惩罚函数定义在约束可行域之外,求解无约束问题的搜索过程是从可行域外部逼近原目标函数的约束最优解的。()此题为判断题(对,错)。
正确答案:√
-
第2题:
用分枝定界法求最大值的整数规划时()。A、分枝后子问题的最优目标函数值可能变大
B、分枝后子问题的最优目标函数值可能不变
C、若某个分枝的最优目标函数值大于其它分支,则该分支得到了最优解
D、以上说法均不对
参考答案:B
-
第3题:
线性规划问题由线性的目标函数和线性的约束条件(包括变量非负条件)组成。满足约束条件的所有解的集合称为可行解区。既满足约束条件,又使目标函数达到极值的解称为最优解。以下关于可行解区和最优解的叙述中,正确的是( )。
A.线性规划问题的可行解区一定存在B.如果可行解区存在,则一定有界C.如果可行解区存在但无界,则一定不存在最优解D.如果最优解存在,则一定会在可行解区的某个顶点处达到
正确答案:D
-
第4题:
求目标函数为极大的线性规划问题时,若全部非基变量的检验数≤O,且基变量中有人工变量时该问题有()
- A、无界解
- B、无可行解
- C、唯一最优解
- D、无穷多最优解
正确答案:B -
第5题:
用最优化方法解决实际问题时,在不同工况下,要确定系统有关回路的()值,以保证目标函数的最优。
- A、设定
- B、控制
- C、目标
- D、约束
正确答案:A -
第6题:
分析无约束最优化问题的数学方法是什么?解决有约束最优化问题的数学方法是什么?
正确答案: 分析无约束最优化问题的数学方法是一元函数求极值方法和多元函数求极值方法。解决有约束最优化问题的数学方法是拉格朗日法和线性规则。 -
第7题:
于多元函数的无约束优化问题,判断其最优点可以根据()。
- A、目标函数的梯度判定
- B、目标函数的性态判定
- C、目标函数的凹凸性判定
- D、目标函数值的大小判定
正确答案:A -
第8题:
贪心法用于求解某目标函数在一定约束条件的最优解。它是从一个可行解(满足约束条件,但未必能使目标函数最优)出发,逐步改进解,以求得最优解的思想方法。但使用贪心法未必一定能够找到最优解。
正确答案:正确 -
第9题:
问答题下表中给出线性规划问题计算过程中某次迭代的单纯形表,目标函数为: ,约束条件均为≤,表中x 4,x 5,x 6为松弛变量,表中目标函数值Z=14。 1 )求出 a-g 的值; 2 )表中给出的解是否为最优解。正确答案: (1)a=7,b=-6,c=0,d=1,e=0,f=1/3,g=0;
(2)表中给出最优解X *=(0 0 7 0 5 0) T。解析: 暂无解析 -
第10题:
判断题贪心法用于求解某目标函数在一定约束条件的最优解。它是从一个可行解(满足约束条件,但未必能使目标函数最优)出发,逐步改进解,以求得最优解的思想方法。但使用贪心法未必一定能够找到最优解。A对
B错
正确答案: 错解析: 暂无解析 -
第11题:
问答题分析无约束最优化问题的数学方法是什么?解决有约束最优化问题的数学方法是什么?正确答案: 分析无约束最优化问题的数学方法是一元函数求极值方法和多元函数求极值方法。解决有约束最优化问题的数学方法是拉格朗日法和线性规则。解析: 暂无解析 -
第12题:
判断题最优化问题的最优解必须满足所有的约束条件A对
B错
正确答案: 对解析: 暂无解析 -
第13题:
若原问题有可行解,但目标函数在可行域上无界,则对偶问题无可行解。()
参考答案:正确
-
第14题:
目标函数为maxZ=28x4+x5+2x6,约束形式为“≤”,且X1X2X3必为松弛变量,表中的解代入目标函数中得Z=12,求出a~g的值.并判断是否最优解。
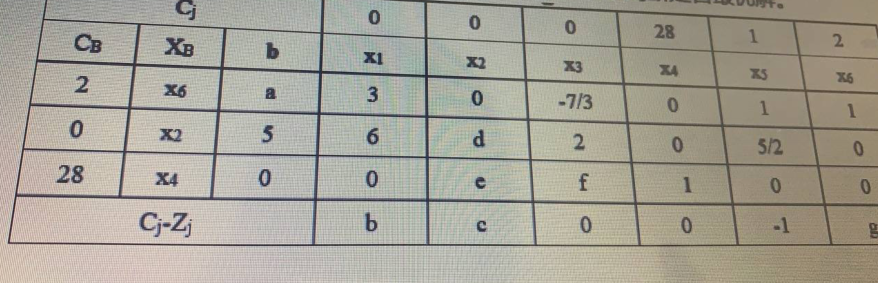 参考答案:
参考答案: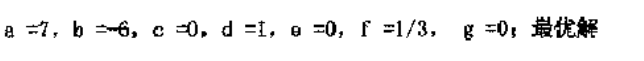
-
第15题:
线性规划问题由线性的目标函数和线性的约束条件(包括变量非负条件)组成。满足约束条件的所有解的集合称为可行解区。既满足约束条件,又使目标函数达到极值的解称为最优解。以下关于可行解区和最优解的叙述中,正确的是(52)。A.线性规划问题的可行解区一定存在
B.如果可行解区存在,则一定有界
C.如果可行解区存在但无界,则一定不存在最优解
D.如果最优解存在,则一定会在可行解区的某个顶点处达到答案:D解析:线性规划问题的求解结果可能出现以下几种情况:得到的最优解是唯一的,无穷多最优解(多重解),无界解(无最优解),无可行解。当求解结果出现后两种情况时,一般说明线性规划问题的数学模型有错误。无界解源于缺乏必要的约束条件,无可行解源于矛盾的约束条件。当线性规划问题的可行域非空时,它是有界或无界凸多边形。若线性规划问题存在最优解,它一定在可行域的某个顶点得到;若在两个顶点同时得到最优解,则它们连线上的任意一点都是最优解,即有无穷多最优解。 -
第16题:
关于最优化控制的叙述正确的是()。
- A、最优化控制的目的在于使目标函数取最大值
- B、控制函数是指工艺参数的限制
- C、变量可由几个到上千个,依具体优化问题而定
- D、如用效果作为目标函数时,最优化问题是求最小值
正确答案:C -
第17题:
用最优化方法解决实际问题时,列出的约束式可以不是等式。
正确答案:错误 -
第18题:
关于线性规划和其对偶规划的叙述中,正确的是()
- A、极大化问题(原始规划)的任意一个可行解所对应的目标函数值是对偶问题最优目标函数值的一个下界
- B、极小化问题(对偶规划)的任意一个可行解所对应的目标函数值是原始问题最优目标函数值的一个下界
- C、若原始问题可行,则其目标函数无界的充要条件是对偶问题有可行解
- D、若对偶问题可行,则其目标函数无界的充要条件是原始问题可行
正确答案:A -
第19题:
外点罚函数法的特点是()
- A、仅适合处理不等式约束的最优化问题
- B、探索过程在可行域内进行
- C、需要先求出初始内点
- D、适合处理等式约束的最优化问题
正确答案:D -
第20题:
用最优化方法解决实际问题时,在不同工况下,要确定有关回路的()值,以保证目标函数的最优.
- A、设定
- B、控制
- C、目标
- D、约束
正确答案:A -
第21题:
单选题求目标函数为极大的线性规划问题时,若全部非基变量的检验数≤O,且基变量中有人工变量时该问题有()A无界解
B无可行解
C唯一最优解
D无穷多最优解
正确答案: A解析: 暂无解析 -
第22题:
单选题用最优化方法解决实际问题时,在不同工况下,要确定有关回路的()值,以保证目标函数的最优.A设定
B控制
C目标
D约束
正确答案: D解析: 暂无解析 -
第23题:
单选题外点罚函数法的特点是()A仅适合处理不等式约束的最优化问题
B探索过程在可行域内进行
C需要先求出初始内点
D适合处理等式约束的最优化问题
正确答案: A解析: 暂无解析 -
第24题:
单选题于多元函数的无约束优化问题,判断其最优点可以根据()。A目标函数的梯度判定
B目标函数的性态判定
C目标函数的凹凸性判定
D目标函数值的大小判定
正确答案: B解析: 暂无解析
