中心极限定理指的是在一定条件下随机变量序列的前n项和近似服从正态分布.

题目

中心极限定理指的是在一定条件下随机变量序列的前n项和近似服从正态分布.

相似考题

1.根据概率论中的中心极限定理,当统计量达到一定程度后,波动是质量特性数据形成一定的分布,并在多数情况下,计量值数据服从()A、正态分布B、泊松分布C、二项分布D、概率分布

2.若随机变量X服从正态分布N(a,b),随机变量Y服从正态分布N(c,d),则X＋Y所服从的分布为正态分布。()此题为判断题(对，错)。

3.设随机变量X1，X2，…，Xn相互独立，Sn=X1+X2+…+Xn，则根据列维一林德伯格中心极限定理，当n充分大时，Sn近似服从正态分布，只要X1，X2，…，Xn( )。A．有相同的数学期望B．有相同的方差C．服从同一指数分布D．服从同一离散型分布

4.关于中心极限定理，下列说法正确的是( )。A．多个随机变量的平均值(仍然是一个随机变量)服从或近似服从正态分布B．几个相互独立同分布随机变量，其共同分布不为正态分布或未知，但其均值μ和方差σ2都存在，则在n相当大的情况下，样本均值X近似服从正态分布N(μ，σ2/n)C．无论什么分布(离散分布或连续分布，正态分布或非正态分布)，其样本均值X的分布总近似于正态分布D．设n个分布一样的随机变量，假如其共同分布为正态分布N(μ，σ2)，则样本均值X仍为正态分布，其均值不变仍为μ，方差为σ2/n

更多“中心极限定理指的是在一定条件下随机变量序列的前n项和近似服从正态分布.”相关问题

  • 第1题：

    关于中心极限定理，下列说法正确的是（ ）。
    A.多个随机变量的平均值（仍然是一个随机变量）服从或近似服从正态分布
    B. n个相互独立同分布随机变量，其共同分布不为正态分布或未知，但其均值μ和方差σ2都存在，则在n相当大的情况下，样本均值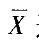
    近似服从正态分布N(μ, σ2/n)
    C.无论什么分布（离散分布或连续分布，正态分布或非正态分布），其样本均值的分布总近似于正态分布
    D.设n个分布一样的随机变量，假如其共同分布为正态分布N(μ, σ2)则样本均值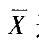仍为正态分布，其均值不变仍为μ，方差为 σ2/n


    答案：B
    解析：
    AC两项成立的前提条件是多个随机变量必须相互独立且同分布；D项要求这些随机变量相互独立。

  • 第2题：

    根据中心极限定理，如果每一随机变量的变异系数小于0.1，则综合后的函数可认为是（）

    • A、正态分布
    • B、泊松分布
    • C、二项分布
    • D、概率密度函数

    正确答案:A

  • 第3题：

    T~N（μσ2）就可以断定这个随机变量近似地服从正态分布。


    正确答案:正确

  • 第4题：

    从一个无限总体中抽取92个观察值作为样本。x-的抽样分布近似于（）。

    • A、正态分布，因为总是近似正态分布
    • B、正态分布，因为相对于总体，样本容量足够大
    • C、正态分布，因为中心极限定理
    • D、以上均错误

    正确答案:D

  • 第5题：

    一个总体有150个个体，从该总体中抽取24个观察值作为样本。x-的抽样分布（）。

    • A、近似正态分布，因为x-总是近似正态分布
    • B、近似正态分布，因为相对于总体，样本容量足够大
    • C、近似正态分布，因为中心极限定理
    • D、如果总体服从正态分布，那它也是正态分布

    正确答案:D

  • 第6题：

    中心极限定理的一般意义是：无论随机变量服从何种分布，只要样本容量足够大，都可以近似地看作是服从（）。

    • A、正态分布
    • B、t分布
    • C、F分布
    • D、X2分布

    正确答案:A

  • 第7题：

    根据中心极限定理，如果每一随机变量的变异系数（），则综合后的函数可认为是正态分布。


    正确答案:v=σ/μ<0.10

  • 第8题：

    设随机变量X服从正态分布N（-1，9），则随机变量Y=2-X服从（）．

    • A、正态分布N（3，9）
    • B、均匀分布
    • C、正态分布N（1，9）
    • D、指数分布

    正确答案:A

  • 第9题：

    多选题
    关于中心极限定理的描述正确的是：（）。
    A

    对于n个相互独立同分布的随机变量共同服从正态分布，则样本均值又仍为正态分布

    B

    正态样本均值服从分布N（μ，σ2/n）

    C

    设X1，X2，„，Xn为n个相互独立共同分布随机变量，其共同分布不为正态分布或未知，但其均值和方差都存在，则在n相当大时，样本均值近似服从正态分布

    D

    无论共同分布是什么，只要变量个数n相当大时，均值的分布总近似于正态分布


    正确答案： C,D
    解析： 暂无解析

  • 第10题：

    多选题
    下列关于德莫佛一拉普拉斯中心极限定理的说法，正确的是
    A

    也称为独立同分布中心极限定理

    B

    给离散型随机变量与连续型随机变量之间的转换提供了一种有效途径

    C

    它的结果表明二项分布的极限分布是正态分布

    D

    当n充分大时，近似的有x～N(np，np(1一p))

    E

    可以利用正态分布近似地计算二项分布的概率


    正确答案： A,D
    解析： 暂无解析

  • 第11题：

    单选题
    根据（），无论总体服从什么分布，只要样本量足够大，来自这个总体的随机样本的均值呈近似正态分布。
    A

    大数定理

    B

    中心极限定理

    C

    最小二乘法

    D

    正态分布特性


    正确答案： D
    解析： 暂无解析

  • 第12题：

    单选题
    中心极限定理的一般意义是：无论随机变量服从何种分布，只要样本容量足够大，都可以近似地看作是服从（）。
    A

    正态分布

    B

    t分布

    C

    F分布

    D

    X2分布


    正确答案： B
    解析： 暂无解析

  • 第13题：

    根据中心极限定理，抽样分布近似于正态分布时样本的规模的判断起点是（）

    A30

    B50

    C70

    D100


    D
    略

  • 第14题：

    中心极限定理告诉我们，不管总体服从什么分布，其（）的分布总是近似服从正态分布。


    正确答案:大容量样本均值

  • 第15题：

    计量型一次抽检方案的理论基础是（）。

    • A、小概率事件原理
    • B、中心极限定理
    • C、切比雪夫定理
    • D、产品的质量特性服从正态分布

    正确答案:D

  • 第16题：

    当总体服从正态，根据（）知道，样本均值也服从正态分布。

    • A、中心极限定理
    • B、正态分布的性质
    • C、抽样分布
    • D、统计推断

    正确答案:B

  • 第17题：

    只要样本容量足够大，样本均值的抽样分布可以用正态概率分布来近似，这一事实基于（）。

    • A、中心极限定理
    • B、我们有正态分布对照表
    • C、假定总体服从正态分布
    • D、以上均错误

    正确答案:A

  • 第18题：

    下列由中心极限定理得到的有关结论中，正确的是（）。

    • A、只有当总体服从正态分布时，样本均值才会趋于正态分布
    • B、只要样本容量n充分大，随机事件出现的频率就等于其概率
    • C、无论样本容量n如何，二项分布概率都可以用正态分布近似计算
    • D、不论总体服从何种分布，只要样本容量n充分大，样本均值趋于正态分布

    正确答案:D

  • 第19题：

    关于中心极限定理的描述正确的是：（）。

    • A、对于n个相互独立同分布的随机变量共同服从正态分布，则样本均值又仍为正态分布
    • B、正态样本均值服从分布N（μ，σ2/n）
    • C、设X1，X2，„，Xn为n个相互独立共同分布随机变量，其共同分布不为正态分布或未知，但其均值和方差都存在，则在n相当大时，样本均值近似服从正态分布
    • D、无论共同分布是什么，只要变量个数n相当大时，均值的分布总近似于正态分布

    正确答案:A,B,C,D

  • 第20题：

    判断题
    T~N（μσ2）就可以断定这个随机变量近似地服从正态分布。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第21题：

    单选题
    下列由中心极限定理得到的有关结论中，正确的是（）。
    A

    只有当总体服从正态分布时，样本均值才会趋于正态分布

    B

    只要样本容量n充分大，随机事件出现的频率就等于其概率

    C

    无论样本容量n如何，二项分布概率都可以用正态分布近似计算

    D

    不论总体服从何种分布，只要样本容量n充分大，样本均值趋于正态分布


    正确答案： A
    解析： 暂无解析

  • 第22题：

    单选题
    设随机变量X服从正态分布N（-1，9），则随机变量Y=2-X服从（）．
    A

    正态分布N（3，9）

    B

    均匀分布

    C

    正态分布N（1，9）

    D

    指数分布


    正确答案： D
    解析： 按定理1，Y是X的线性函数，y依然服从正态分布，由k=-1、c=2算得y服从正态 分布 N（2-(-1)，（-1)2×9)=N(3,9). 故选(A).

  • 第23题：

    单选题
    设随机变量X和Y都服从正态分布，则（　　）。
    A

    X＋Y一定服从正态分布

    B

    X和Y不相关与独立等价

    C

    （X，Y）一定服从正态分布

    D

    （X，－Y）未必服从正态分布


    正确答案： C
    解析：
    用排除法，令Y＝－X，则X＋Y＝0不服从正态分布，故排除A项；
    只有X，Y的联合分布服从正态分布时，X，Y不相关才与X，Y相互独立等价，故排除B项；
    一般边缘分布不决定联合分布，故选排除C项；故应选D。

  • 第24题：

    填空题
    中心极限定理告诉我们，不管总体服从什么分布，其（）的分布总是近似服从正态分布。

    正确答案： 大容量样本均值
    解析： 暂无解析

相关内容