约束项和任意项统称为逻辑函数中的 项，在卡诺图中用“×”表示。

题目

约束项和任意项统称为逻辑函数中的 项，在卡诺图中用“×”表示。

相似考题

1.约束项就是逻辑函数中不允许出现的变量取值组合,用卡诺图化简时,可将约束项当作,也可当作0。()

2.输入无反变量函数F的化简，讨论的是___。A、函数F的标准与或式B、用禁止逻辑法寻找F的共享禁止项C、函数F中不能出现非运算D、在F的卡诺图上所有的质蕴涵

3.用卡诺图化简具有无关项的逻辑函数时，若用圈1法，在包围圈内的´是按处理;在包围圈外的´是按______处理。A、1，1B、1，0C、0，0D、不确定。

4.表示逻辑函数通常使用真值表、逻辑函数、卡诺图、逻辑图及工作波形图。 ()此题为判断题(对，错)。

更多“约束项和任意项统称为逻辑函数中的 项，在卡诺图中用“×”表示。”相关问题

  • 第1题：

    逻辑函数的表示方法?_________

    A.逻辑状态表

    B.逻辑式

    C.逻辑图

    D.卡诺图


    正确答案:ABCD

  • 第2题：

    变量卡诺图尽管形象地表示了变量最小相的逻辑上的相邻性，但它也有缺点就是( )。

    A.随着变量的增加，图形会迅速地复杂起来;

    B.卡诺图只适用于10个变量以内的逻辑函数;

    C.逻辑上相邻但数据上不相邻;

    D.除逻辑函数中的最小项外，有很多多余的最小项


    正确答案：A

  • 第3题：

    试用 卡诺图化简如下逻辑函数式。


    答案：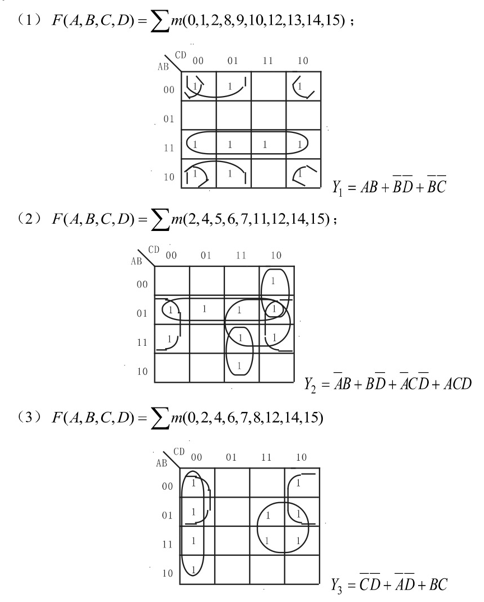

  • 第4题：

    下列说法，哪一个不是逻辑函数的表示方法？( )

    A.真值表和逻辑表达式
    B.卡诺图和逻辑图
    C.波形图和状态表

    答案：C
    解析：
    逻辑函数的表示方法有：真值表、逻辑表达式、卡诺图、逻辑图和波形图，一般不用状态表来表示逻辑函数。

  • 第5题：

    逻辑函数的表示方法（ ）

    A.真值表 B.逻辑代数式 C.卡诺图 D.逻辑电路图

    答案：A,B,C,D
    解析：

  • 第6题：

    逻辑函数的描述方法有真值表法、（）、（）和卡诺图法。


    正确答案:逻辑式；逻辑电路图

  • 第7题：

    下列说法中，（）不是逻辑函数的表示方法。

    • A、真值表和逻辑表达式
    • B、卡诺图和逻辑图
    • C、波形图和状态图

    正确答案:C

  • 第8题：

    用卡诺图化简逻辑函数的步骤除了将函数化简为最小项之和的形式外还有（）。

    • A、画出表示该逻辑函数的卡诺图
    • B、找出可以合并的最小项
    • C、写出最简“与或”逻辑函数表达式
    • D、写出最简“与或非”逻辑函数表达式

    正确答案:A,B,C

  • 第9题：

    常用的逻辑函数的表示方法有（）。 

    • A、逻辑函数表达式
    • B、真值表
    • C、卡诺图
    • D、逻辑图
    • E、时序图
    • F、符号图

    正确答案:A,B,C,D

  • 第10题：

    表示逻辑函数功能的常用方法有（）等。

    • A、真值表
    • B、逻辑图
    • C、波形图
    • D、卡诺图
    • E、状态图

    正确答案:A,B,C,D

  • 第11题：

    多选题
    常用的逻辑函数的表示方法有（）。
    A

    逻辑函数表达式

    B

    真值表

    C

    卡诺图

    D

    逻辑图

    E

    时序图

    F

    符号图


    正确答案： C,D
    解析： 暂无解析

  • 第12题：

    单选题
    用卡诺图简化具有无关项的逻辑函数时，若用圈“1”法，在包围圈内的X和包围圈外的X分别按（　　）处理。[2007年真题]
    A

    1，1

    B

    1，0

    C

    0，0

    D

    无法确定


    正确答案： B
    解析：
    在实际的逻辑电路中，经常会遇到某些最小项的取值可以是任意的，或者这些最小项在电路中根本是不会出现的，这样的最小项称为无关项。在卡诺图和真值表中用Φ表示，它们的取值可以为0或1，在进行函数化简时包围圈内的无关项按“1”处理，包围圈外的无关项按“0”处理。

  • 第13题：

    简述逻辑函数的卡诺图化简法的主要原则。


    答案：卡诺图化简法(reduced method of a Karnaugh map)是化简真值函数的方法之一，它具有几何直观性这一明显的特点，在变元较少(不超过六个)的情况下比较方便，且能得到最简结果。

    此法由卡诺(M.Karnaugh)于1953年提出，其具体步骤如下：

    1，构造卡诺框；

    2，在卡诺框上做出所给真值函数f的卡诺图；

    3，用卡诺图化简真值函数，首先把相邻的1字块两两合成矩形得到一维块；把22个相邻的1字块合成矩形(或正方形)得到二维块;把23个相邻的1字块合成矩形得到三维块等，合成的各种维块统称f的合块；

    4，把f的卡诺图中全部1字块做成若干个合块，这样一组合块就称为f的一个覆盖组，f的一切覆盖组中所含块数最小的组即是f的最小覆盖组；

    5，在最小覆盖组中，合块维数总和最大的组的对应式是f的最简式

    画卡诺圈所遵循的原则如下：

    (1)必须包含所有的最小项；

    (2)按照“从小到大”顺序，先圈孤立的“1”．再圈只能两个组合的，再圈四个组合的。

    (3)圈的圈数要尽可能少(乘积项总数要少)。

    (4)圈要尽可能大(乘积项中含的因子最少)。

    无论是否与其他圈相重，也要尽可能画大，相重是指在同一块区域可以重复圈多次，但每个圈至少要包含一个尚未被圈过的“1”。


  • 第14题：

    试用卡诺图化简如下具有任意项的逻辑函数式。


    答案：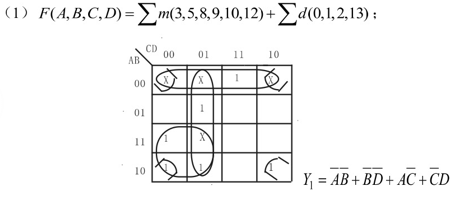

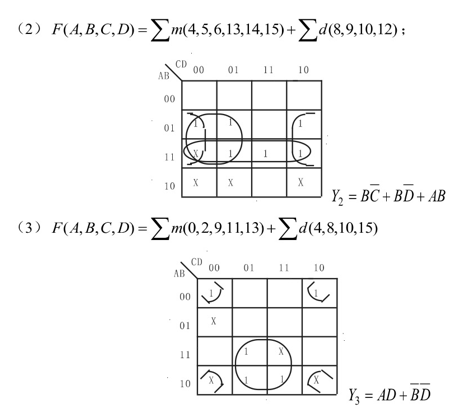
  • 第15题：

    已知用卡诺图化简逻辑函数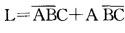的结果是L=A十C，那么该逻辑函数的无关项至少有（ ）。
    A. 2个 B. 3个 C. 4个 D.5个


    答案：C
    解析：
    解将用卡诺图表示如图a)所示。将L=A十C用卡诺图表示如图b)所示，可见无关项至少4项。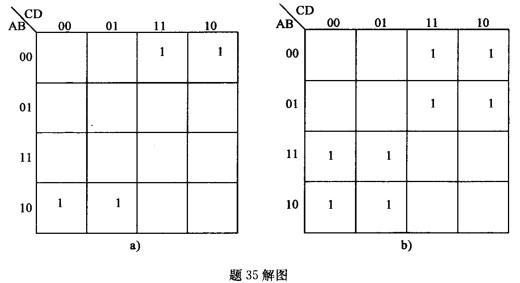

    答案：C

  • 第16题：

    用卡诺图简化具有无关项的逻辑函数时,若用圈"1"法,在包围圈内的x和包围圈外的x分别按下列哪项处理？
    （A）1、1 （B）1、0
    （C）0、0 （D）无法确定


    答案：B
    解析：
    解：选B。包围圈内的无关项按"1"处理，包围圈外的无关项按"0"处理。

  • 第17题：

    下列说法，（）不是逻辑函数的表示方法。

    • A、真值表和逻辑表达式
    • B、卡诺图和逻辑图
    • C、波形图和状态图
    • D、真值表和逻辑图

    正确答案:C

  • 第18题：

    卡诺图化简逻辑函数有何优缺点？


    正确答案:卡诺图法直观但不适合变量多的函数化简。

  • 第19题：

    逻辑函数的表示方法中具有唯一性的是（）

    • A、真值表
    • B、表达式
    • C、逻辑图
    • D、卡诺图

    正确答案:A,D

  • 第20题：

    下列说法错误的是（）。

    • A、逻辑函数的表达方法有真值表、逻辑表达式、逻辑图和卡诺图
    • B、真值表是将逻辑函数的最小项按一定规律排列成正方形或矩形
    • C、有了某函数的一种表示方法，就可以转换成其他表示方法
    • D、在电路的分析设计中，一般先列写真值表，再根据真值表列写出函数关系式

    正确答案:B

  • 第21题：

    （）是逻辑函数中的无关项。

    • A、变量项
    • B、加减项
    • C、约束项和任意项
    • D、最小项

    正确答案:C

  • 第22题：

    用卡诺图简化逻辑函数的正确方式是：（）

    • A、将函数化为最小项之和的形式。
    • B、画出表示该逻辑函数的卡诺图。
    • C、找出可以合并的最大项。
    • D、选取化简后的乘积项。

    正确答案:A,B,D

  • 第23题：

    单选题
    下列选项中，（）不是逻辑函数的表示方法。
    A

    真值表和逻辑表达式

    B

    卡诺图和逻辑图

    C

    波形图和状态图


    正确答案： C
    解析： 暂无解析

  • 第24题：

    多选题
    逻辑函数的表示方法中具有唯一性的是（）。
    A

    真值表

    B

    表达式

    C

    逻辑图

    D

    卡诺图


    正确答案： C,D
    解析： 暂无解析

相关内容