一个公比为2的等比数列，第n项与前n-1项和的差等于3，则此数列的前4项之和为:A.54 B.45 C.42 D.36

题目
一个公比为2的等比数列，第n项与前n-1项和的差等于3，则此数列的前4项之和为:



A.54
B.45
C.42
D.36
相似考题

1.已知等差数列{an}的首项与公差相等，{an）的前n项的和记作Sn，且S20=840．（I）求数列{an}的首项a1及通项公式；（Ⅱ）数列{an}的前多少项的和等于847.

2.已知数列{an}的前n项和Sn=n2-2n．求（I）{an}的前三项；（II）{an}的通项公式．

3.已知数列{an}的通项公式为an =(4 9) n-1 - (2 3) n-1 (n ∈ N∗ ),则数列{an}( ).(A)有最大项,没有最小项.(B)有最小项,没有最大项.(C)既有最大项又有最小项.(D)既没有最大项也没有最小项.

4.已知公比为q的等比数列{an）中，a2=4，a5=-32．（I）求q；（11）求{an}的前6项和S6．

更多“一个公比为2的等比数列，第n项与前n-1项和的差等于3，则此数列的前4项之和为: ”相关问题

  • 第1题：

    已知等差数列{an}中，a1=21，Sn是它的前n项之和，S7=S15。
    (1)求Sn；
    (2)这个数列的前多少项之和最大 求出最大值。


    答案：
    解析：
    (1)设等差数列的公差为d，由题意可得：



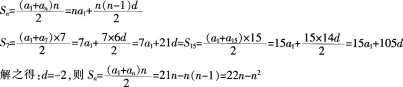
    (2)Sn=22n-n2=-(n-11)2+121，当n=11时，数列之和最大，最大值为121。

  • 第2题：

    —个公比为2的等比数列，第n项与前n-1项和的差等于5，则此数列前4项之和为：

    A.70
    B.85
    C.80
    D.75

    答案：D
    解析：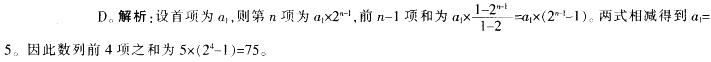

  • 第3题：

    已知等比数列{an}的各项都是正数，且a1+a3=10，a2+a3=6．
    (Ⅰ)求{an}的通项公式；
    (Ⅱ)求{an}的前5项和．


    答案：
    解析：
    解:(Ⅰ)设(an)的公比为q，由已知得

  • 第4题：

    已知数列{an｝中，Sn是它的前n项和，并且Sn+1=4an+2,a1=1．
    (Ⅰ)设bn=an+1-2an，求证：数列{bn)是等比数列；
    (Ⅱ)设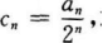求证：数列{cn}是等差数列；
    (Ⅲ)求数列｛an｝的通项公式及前n项和．


    答案：
    解析：



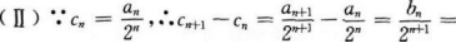
  • 第5题：

    已知首项为1的无穷递缩等比数列的所有项之和为5,q为公比,则q=（ ）

    A.2/3
    B.-2/3
    C.4/5
    D.-4/5
    E.1/2

    答案：C
    解析：

  • 第6题：

    一个等差数列的前12项的和为354,前12项中偶数项之和与奇数项之和的比是32:27,则其项数为（ ）

    A.3
    B.4
    C.5
    D.6
    E.7

    答案：C
    解析：

  • 第7题：

    下面是人教版普通高中数学教科书必修5的内容，据此回答下列问题。




    问题：
    (1)请说明教材中引用故事的意图；(6分)
    (2)写出这节课的教学重难点；(6分)
    (3)在等比数列前n项和公式推导的过程用了什么方法，说明应用这种方法条件；(6分)
    (4)请为教材中第一个思考“当q=1时，等比数列的前n项和Sn等于多少”设计一个教学片段。(12分)


    答案：
    解析：
    (1)教材中用一个古老但又具体的故事，为了让学生了解学习“等比数列求前n项和”在解决生活中问题的必要性，用一个有趣的问题激发学生的好奇心和求知欲。(2)教学重点：掌握等比数列前n项和公式，及利用公式解决问题；
    教学难点：数列前n项和公式的推导。
    (3)在等比数列前n项和公式推导过程中用的方法是“错位相减法”。错位相减法是一种常用的数列求和方法，应用于等比数列与等差数列相乘的形式。比如，在教材中，等比数列前n项和公式推导过程中，表示出等比



    (4)教学片段：



    生：q=1时，公式里的分母等于零了，没有意义了。
    师：没错，只有在q≠1时上述公式才成立。那么如果一个等比数列，公比q=1，那它的前n项和怎么求呢?
    生：如果公比q=1，则这个等比数列就是常数列，每一项都相等……
    师：所以，当q=1时，前n项和等于……
    生：na1
    师：很好。所以大家在理解和记忆等比数列前n项和的时候，就要明确它是由两部分组成的，一部分是……
    生：q≠1时。
    师：另一部分是……
    生：q=1时。
    师：很好。大家在以后做题时遇到等比数列求和问题就要想想，公比q的取值。

  • 第8题：

    设an=n2-9n-100(n=1，2，3…)，则数列{an}中取值最小的项为( )。

    A、第4项
    B、第5项
    C、第6项
    D、第4和第5项

    答案：D
    解析：
    将数列％看做一个一元二次多项式，开口向上在对称轴n=4．5处取得最小值。但是数列中n为正整数，故在其附近找最小值。当n=4时，an=-120；当n=5时，an=-120。故取最小值的项为第4项和第5项。故选D。

  • 第9题：

    (10分)已知数列{an}的前n项和Sn=2n+1-k(其中k为常数)：
    (1)求数列{ an }的通项公式；(4分)
    (2)若a1=2，求数列{n an }的前n项和Tn。(6分)


    答案：
    解析：

  • 第10题：

    请用悬念导入法给“等比数列前n项和”这节课设计一个课堂导入。


    正确答案:我将从“折纸”这种常见的活动出发，让学生体会一张薄薄的纸片只需对折不多的次数，其厚度就会大幅增长。我首先拿一张纸条，厚0.1毫米，然后把纸条一次又一次地对折，厚度当然越来越厚，然后我这样告诉同学，这样对折14次，厚度可达同学们的身高；对折27次后，其厚度比珠穆朗玛峰还要高；对折42次后，厚度超过从地球到月球的距离。接着我问同学们：“大家相信吗？如果要使厚度达到从地球到太阳的距离（1.5亿km），需要对折多少次呢？”（两次设疑，会立即引起学生的积极思考。）

  • 第11题：

    单选题
    一个数列，前两项是1，从第三项开始，每一项都等于前两项之和，称为：（）。
    A

    求和数列

    B

    加和数列

    C

    子空间数列

    D

    斐波那契数列


    正确答案： B
    解析： 暂无解析

  • 第12题：

    问答题
    请用悬念导入法给“等比数列前n项和”这节课设计一个课堂导入。

    正确答案： 我将从“折纸”这种常见的活动出发，让学生体会一张薄薄的纸片只需对折不多的次数，其厚度就会大幅增长。我首先拿一张纸条，厚0.1毫米，然后把纸条一次又一次地对折，厚度当然越来越厚，然后我这样告诉同学，这样对折14次，厚度可达同学们的身高；对折27次后，其厚度比珠穆朗玛峰还要高；对折42次后，厚度超过从地球到月球的距离。接着我问同学们：“大家相信吗？如果要使厚度达到从地球到太阳的距离（1.5亿km），需要对折多少次呢？”（两次设疑，会立即引起学生的积极思考。）
    解析： 暂无解析

  • 第13题：

    一个公比为2的等比数列，第n项与前n-1项和的差等于3，则此数列的前4项之和为:



    A.54
    B.45
    C.42
    D.36

    答案：B
    解析：
    设首项为a1，则第n项为a1×2 n-1，前n-1项和为两式相减得到a1 =3，因此数列前四项之和为3×（24-1）=45.

  • 第14题：

    已知等比数列{an}的各项都是正数，且a1+a3=10，a2+a3=6．
    (I)求{an}的通项公式；
    (II)求{an)的前5项和．


    答案：
    解析：

  • 第15题：

    已知一个等差数列的第五项等于10，前三项的和等于3，那么这个等差数列的公差为（ ）

    A.3
    B.1
    C.-1
    D.-3

    答案：A
    解析：

  • 第16题：

    一个无穷等比数列所有奇数项之和为45,所有偶数项之和为-30,则其首项等于（ ）

    A.24
    B.25
    C.26
    D.27
    E.28

    答案：B
    解析：

  • 第17题：

    已知数列{an}的通项公式为an=2n,数列{bn}的通项公式为bn=3n+2.若数列{an}和{bn}的公共项顺序组成数列{cn},则数列{cn}的前3项之和为（ ）

    A.248
    B.168
    C.128
    D.19
    E.以上选项均不正确

    答案：B
    解析：

  • 第18题：

    高中数学《等比数列前n项和》
    一、考题回顾
    题目来源：5月19日 上午 重庆市 面试考题
    试讲题目
    1.题目：等比数列前n项和
    2.内容：



    3.基本要求：
    (1)引导学生应用等比数列前n项和;
    (2)试讲10分钟;
    (3)合理设计板书;
    (4)要有适当的提问互动环节。
    答辩题目
    1.等差数列的前n项和公式是什么?
    2.怎样才能设计好授课板书呢?你能给出几点建议吗?


    答案：
    解析：
    二、考题解析
    【教学过程】
    (一)引入新课
    复习等差数列前n项和公式。提问：等比数列前n项和怎么求呢?有没有相应的公式呢?
    引出课题。
    (二)探索新知


  • 第19题：

    已知{an}是由非负整数组成的无穷数列，该数列前n项的最大值记为A。第项之后各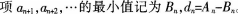
    (1)若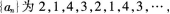是一个周期为4的数列(即对任意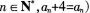写出dl，dz,d3，d0的值；
    (2)设d为非负整数，证明：do=一d(n=1，2，3…)的充分必要条件为{an}为公差为d的等差数列：
    (3)证明：若a1=2，dn=1(n=1，2，3，…)，则{an}的项只能是1或者2，且有无穷多项为l。


    答案：
    解析：

  • 第20题：

    已知数列{％}的前n项和是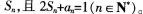
    (1)求证：数列{an}是等比数列：
    (2)记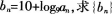的前n项和Tn的最大值及相应的n值。


    答案：
    解析：

  • 第21题：

    已知数列{an}的前n项和是Sn，且2Sn+an=1(n∈N*)。
    (1)求证：数列{an}是等比数列；
    (2)记bn=10+log9an，求{bn}的前n项和Tn的最大值及相应的n值。


    答案：
    解析：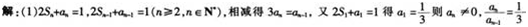


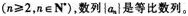
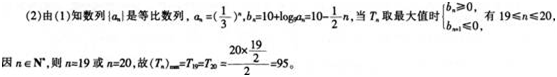
  • 第22题：

    在移动平均中，设移动n年则（）。

    • A、当n为偶数时，移动后所得新数列较原数列首尾各缺n∕2项
    • B、当n为奇数时，移动后所得新数列较原数列首尾缺（N-1）∕2项
    • C、当n为偶数时，移动后所得新数列较原数列首尾缺n项
    • D、当n为奇数时，移动后所得新数列较原数列首尾缺n项

    正确答案:A,B

  • 第23题：

    单选题
    数据结构与算法里，设fun（n）表示斐波那契数列的第n项的值，fun是函数名，n是整型参数，那么根据递归思想它应等于（）。
    A

    fun（n）+fun（n-1）

    B

    fun（n-1）+fun（n-2）

    C

    fun（n-1）*fun（n-2）

    D

    fun（n-2）+fun（n-3）


    正确答案： D
    解析： 暂无解析

  • 第24题：

    问答题
    在考生文件夹下有一个工程文件sjt5.vbp。其功能是产生并显示一个数列的前n项。数列产生的规律是：数列的前2项是小于10的正整数，将此两数相乘，若乘积<10，则以此乘积作为数列的第3项，若乘积≥10，则以乘积的十位数为数列的第3项，以乘积的个位数为数列的第4项。再用数列的最后两项相乘，用上述规则形成后面的项，直至产生了第n项。窗体上部从左到右3个文本框的名称分别为Text1、Text2、Text3，窗体下部的文本框名称为Text4。程序运行时，在Text1、Text2中输入数列的前两项，Text3中输入要产生的项数n，单击“计算”按钮则产生此数列的前n项，并显示在Text4中。如下图所示。　　程序提供代码　　　　　　已经给出了全部控件，但程序不完整，请去掉程序中的注释符，把程序中的“?”改为正确的内容。　　注意：不得修改原有程序和控件的属性。最后把修改后的文件按原文件名存盘。

    正确答案： 步骤1:打开本题工程文件。
    步骤2:打开代码编辑窗口,去掉程序中的注释符“'”,将问号改为正确的内容。
    第1个?处填入:h
    第2个?处填入:b
    第3个?处填入:n
    第4个?处填入:b
    步骤3:调试并运行程序,关闭程序后按题目要求存盘。
    解析： 暂无解析

相关内容