某训练基地的一块三角形场地的面积是1920平方米。已知该三角形场地的三边长度之比是5:12:13，则其周长是：A.218米 B.240米 C.306米 D.360米
题目
B.240米
C.306米
D.360米
相似考题
更多“某训练基地的一块三角形场地的面积是1920平方米。已知该三角形场地的三边长度之比是5:12:13，则其周长是：”相关问题
-
第1题：
若一个三角形的所有边长都是整数，其周长是偶数，且已知其中的两边长分别为10和2000，则满足条件的三角形总个数是（ ）。
A.10 B.7 C.8 D.9
.【答案】D。解析：周长为偶数，其中的两边长为偶数，则第三条边长也为偶数，根据两边之和大于第三边，两边之差小于第三条边，得第三条边长是满足1990x2010的偶数，共9个
-
第2题：
某三角形的三边长分别为3、4、5，则该三角形的面积与周长之比为( )。
A．2:1
B．3:1
C．1:2
D．1:3
正确答案：C
10． C [本题考点] 这是一道“几何”类型的题目。考查的知识点有：三角形的面积、周长的计算公式和勾股定理。
[解题思路] 对勾股定理掌握熟练的考生很容易发现：3、4、5恰好是直角三角形的三边，所以面积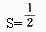
×3×4=6，而周长C=3+4+5=12，两者之比为1:2。除了三角形的面积周长公式外，考生还应掌握常见图形的面积和周长公式，如圆、正方形、长方形等。
-
第3题：
已知一直角三角形的一个直角边长为12，且周长比面积的数值小18，则该三角形的面积是（ ）。
A．20
B．36 >>>>>
C．54
D．96
正确答案：C
-
第4题：
已知三角形的两边长分别为4cm和9cm，则下列长度的四条线段中能作为第三边的是（ ）
A．13cm B．6cm C．5cm D．4cm
正确答案：B
-
第5题：
已知三角形的两边长分别为3cm和8cm，则此三角形的第三边边长可能是().?A.4cm
B.5cm
C.6cm
D.13cm答案：C解析：分别令三角形的三边长为a、b、c，则有a=3，b=8，我们由三角形的两边之和大于第三边，两边之差小于第三边得到a+b>c，b-a第6题：
已知三角形三边长分别为3、15、X。若X为正整数，则这样三角形有多少个：
A3个
B4个
C5个
D无数个答案：C解析：
第7题：
某训练基地的一块三角形场地的面积是1920平方米。已知该三角形场地的三边长度之比是5:12:13，则其周长是：A.218米
B.240米
C.306米
D.360米答案：B解析：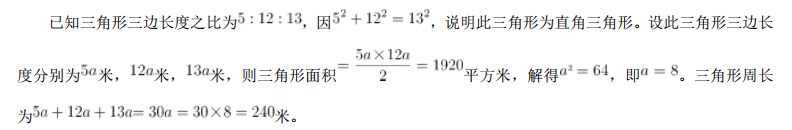
第8题：
若一直角三角形的周长与面积的数值相等，且两直角边长之和为14，则该三角形的面积是（）。A.20
B.24
C.12
D.6.2答案：B解析：两个直角边和为14，直角边中至少有一个大于等于7。根据斜边长度大于任意直角边，可知斜边大于7。则周长大于21。周长与面积相等，直接选B。第9题：
如图2，已知△ABC的周长为1，连接△ABC三边的中点构成第二个三角形，再连接第二个三角形三边中点构成第三个三角形，依次类推，第2008个三角形的周长为（ ）
答案：C解析：第10题：
已知三角形三边长分别为2，x，13，若x为正整数，则这样的三角形个数为（ ）
A.2
B.3
C.5
D.13答案：B解析：
第11题：
已知三角形三边长分别为2，x，13，若x为正整数，则这样的三角形个数为（）
- A、2
- B、3
- C、5
- D、13
正确答案:B第12题：
单选题已知三角形内的一个点到它的三边距离相等，那么这个点是（ ）．A三角形的外心
B三角形的重心
C三角形的内心
D三角形的垂心
正确答案： D解析： 暂无解析第13题：
程序Cmody071.c,其功能是从键盘输入三角形的三边长,求其面积,若三个边长不能构成三角形,则提示。请改正错程序中的错误。如 输入:6 9 11输出:26.98
/**/&a[i]/**/
/**/if（a[0]+a[1]>a[2]&&a[1]+a[2]>a[0]&&a[0]+a[2]>a[1]）/**/第14题：
若一直角三角形的周长与面积的数值相等，且两直角边长之和为14，则该三角形的面积是（ ）。
A．20
B．24
C．12
D．6.2 ( ⊙o⊙ )
正确答案：B
第15题：
三角形的三边长分别为5，1+2x，8，则x的取值范围是________.
正确答案：
1x6.点拨：9－51+2x8+5，解得1x6；第16题：
一块三角形农田ABC（如下图所示）被DE、EF两条道路分为三块。已知BD＝2AD，CE＝2AE，CF＝2BF，则三角形ADE、三角形CEF和四边形BDEF的面积之比为：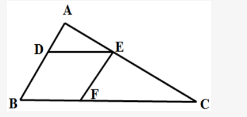
A.1∶3∶3
B.1∶3∶4
C.1∶4∶4
D.1∶4∶5答案：C解析：解法一：
第一步，本题考查几何问题，属于平面几何类，用比例法解题。
第二步，由BD＝2AD，CE＝2AE，CF＝2BF，则DE∥BC，EF∥AB，即四边形BDEF是平行四边形，可得BD＝EF，DE＝BF。△ADE与△EFC与△ABC相似，所以边长比的平方等于面积比，所以
因此三角形ADE与四边形BDEF的面积比为1∶4，所以三者比值为1∶4∶4。
因此，选择C选项。
解法二：
第一步，本题考查几何问题，属于平面几何类，用代入排除法解题。
第二步，由题意知，△ADE与△ABC相似，且AD∶AB＝1∶3，根据几何比例关系，＝1∶9。代入A选项，1∶（1＋3＋3）＝1∶7≠1∶9，排除；代入B选项，1∶（1＋3＋4）＝1∶8≠1∶9，排除；代入C选项，1∶（1＋4＋4）＝1∶9，满足；代入D选项，1∶（1＋4＋5）＝1∶10≠1∶9，排除。第17题：
如图，在长方形ABCD中，已知三角形ABE、三角形ADF与四边形AECF的面积相等，则三角形AEF与三角形CEF的面积之比是
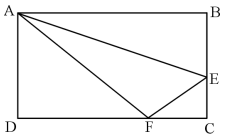A.5∶1
B.5∶2
C.5∶3
D.2∶1答案：A解析：第一步，三角形ABE、三角形ADF与四边形AECF的面积相等，则三者各占长方形ABCD面积的1/3。连接辅助线AC，则三角形ACD的面积为长方形的1/2。?
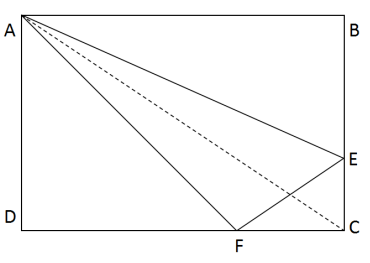
第二步，三角形ADF与三角形ACD的高相同，都为AD，三角形高相同，底边之比等于面积之比，则FD：CD＝2：3，所以CF＝1/3CD，同理CE＝1/3BC，因此三角形CEF的面积为长方形面积的1/18，则三角形AEF的面积为长方形面积的1/3－1/18＝5/18，所以两者面积之比为5：1。解法二：赋值长方形的长为6，宽为3，则长方形的面积为18。三角形ABE、三角形ADF与四边形AECF的面积相等，则三者的面积各为6。那么FD的长为4，CF长2，则CE的长为1，则三角形CEF的面积为1，三角AEF的面积为6－1＝5，则两者的面积之比为5：1。因此，选择A选项。第18题：
一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形面积的（ ）。
答案：B解析：依题意，一个正三角形和一个正六边形周长相等，所以正三角形的边长为正六边形边长的2倍，正三角形可以划分为4个边长为其一半的全等的小正三角形，正六边形可以划分为边长与其相等的6个全等的小正三角形，所以正六边形的面积为正三角形的1. 5倍。第19题：
某健身馆准备将一块周长为100米的长方形区域划为瑜伽场地，将一块周长为160米的长方形区域划为游泳场馆。若瑜伽场地和游泳场馆均是满足周长条件下的最大面积，问两块场地面积之差为多少平方米？A.625
B.845
C.975
D.1150答案：C解析：第一步，本题考查几何问题，用几何最值理论解题。
第二步，四边形周长固定，越接近于正方形面积则面积越大。周长为100米的四边形，当其为正方形时面积最大，故正方形边长为100÷4＝25（米），面积为252＝625（平方米）；周长为160米的四边形，当其为正方形时面积最大，故正方形边长为160÷4＝40（米），面积为402＝1600（平方米）。
第三步，两块场地面积之差为1600－625＝975（平方米）。第20题：
两个等腰三角形如图6-12所示叠放在一块,已知BD=6,DC=4,则重合部分的阴影面积为
A.13
B.14
C.15
D.16
E.17答案：E解析：
第21题：
如下图，把三角形ABC 的三边分别延长1、2、3 倍，得到一个新的三角形，则新三角形的面积是原三角形ABC 面积的几倍？（ ）
A、15
B、16
C、17
D、18答案：D解析：
第22题：
已知三角形三边长分别为3、15、X。若X为正整数，则这样三角形有多少个？
- A、3个
- B、4个
- C、5个
- D、无数个
正确答案:C第23题：
填空题若两个相似三角形的周长比为2∶3，则它们的面积比是____．正确答案： 4∶9解析：
相似三角形的面积比是周长比的平方．第24题：
单选题已知三角形三边长分别为3、15、X。若X为正整数，则这样的三角形有多少（ ）A3个
B4个
C5个
D无数个
正确答案： D解析：