有人测量一座桥离水面的高度,将一根绳子对折,碰到水面时绳子还剩下 6 米(按对折 后的长度算);把绳子平均折成三段,碰到水面时绳子还剩下 2 米。 问桥高多少米 A.2 B.4 C.6 D.8
题目
B.4
C.6
D.8
相似考题
参考答案和解析
更多“有人测量一座桥离水面的高度,将一根绳子对折,碰到水面时绳子还剩下 6 米(按对折 后的长度算);把绳子平均折成三段,碰到水面时绳子还剩下 2 米。 问桥高多少米 ”相关问题
-
第1题:
用一根绳子测量一条路的宽度,当绳子两折时,多出5米;当绳子三折时,还差2米。那么路宽( )米。
A.16
B.12
C.7
D.21
正确答案:A
A [解析]设路宽x米,根据题意可知:2(x+5)=3(x-2),解得x=16,即路宽16米。 -
第2题:
一根绳子,第一次剪去全长的九分之五 ,第二次剪去的长度与第一次剪去长度的比是9∶20,结果还剩下7米,求这条绳子的长是多少米?()
A. 18
B. 26
C. 32
D. 36
-
第3题:
用绳子测量井深,把绳子 3 折后,井外多出 4 米,把绳子 4 折后,井外多出 1 米,问井深多少米?( )
A.3
B.8
C.12
D.36
正确答案:B
-
第4题:
有两根绳子, 长的比短的长1倍, 现在把每根绳子都剪掉6分米, 那么长的一根就比短的一根长两倍。长绳子为短绳子的多少倍?( )
A.1
B.2
C.3
D.4
正确答案:B
32.B[解析]设短绳子为X分米,则长绳子为(1+1)X分米,列方程得(1+1)X一6=(x一6)×(1+2)
解得:x=12 7
长绳子为:12×(1+1)=24(分米)24÷12=2,因此本题正确答案为B。 -
第5题:
用一根绳子测井台到井水面的深度,把绳对折后垂到井水面,绳子超过井台9米,把绳子三折后垂到井水面,绳子超过井台2米,绳长为多少?( )
A.12米
B.29米
C.36米
D.42米
正确答案:D
23.【答案】D 根据题意可知,(9-2)÷(1/2-1/3)=42,绳长为42米,选择D。 -
第6题:
用绳子量桥高,在桥上将绳子4折垂至水面,余3米;把绳子剪去6米,3折后,余4米。桥高是多少米?( )
A.36
B.12
C.9
D.6
正确答案:D
14.D【解析】设桥高z米, 依绳子长度不变可列方程为:4(z+3)一3(z+4)+6,解得,2一6。 -
第7题:
在桥上用绳子测量桥的高度,把绳子对折垂到水面时尚余8m,把绳子三折垂到水面尚余2m,求桥高和绳长( )。
A.36 12
B.10 36
C.12 36
D.10 35
正确答案:B
根据题意,绳子长度比桥高的2倍还多8×2=16(m);
绳子长度比桥高的3倍还多2×3=6(m)。
所以桥的高度为16-6=10(m),绳子的长度为2×10+16=36(m)。故选B。 -
第8题:
用绳子测枯井的深度。绳子折成三段时,多余20厘米;绳子折成四段时,还差35厘米。绳长多少厘米?( )
A.560 B.600 C.640 D.660
正确答案:D选D。设绳长为x,则根据题意有 x/3 - 20= x/4 +35,所以x=660.
-
第9题:
一根绳子用去它的3/5,还剩下3/5米,则()。A.用去的绳子较长
B.剩下的绳较长
C.用去的与剩下的一样长
D.无法确定答案:A解析: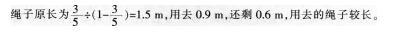
-
第10题:
你一番判断之后,终于找到了应该受奖励的小徒弟。这时老者拿起书案上的一根细绳,先把绳子对折三次,然后把对折后的绳子剪成了三段。笑眯眯的看着你说:“请问智者,现在我这有多少段绳子?”
你应该如何回答老者呢?
现在老者那里一共有__________段绳子。答案:解析:7。 -
第11题:
用一根绳子测量一口枯井的深度,如果绳子对折去量就多出4米,三折去量就多出1米,则该井的深度是:A.6米
B.5米
C.4米
D.3米答案:B解析:设井深度为x米,第一次是对折,第二次是三折,则有2x(x+4)=3x(x+1),解得x=5。 -
第12题:
用一根绳子测量井的周长,绳子绕井口三周还余1米;将绳子对折后量,绕井口一周还余2米。这根绳子长多少米?( )A.10
B.12
C.13
D.15答案:A解析:本题属于数字特性问题。
根据题意:“绕井口三周还余1米,对折绕井口一周还余2米”可知为数字特性类题目。答案减去1应该为3的倍数,排除B、D选项;代入A选项,符合题干。 -
第13题:
将一根绳子连续对折3次,然后每隔一定长度剪一刀,并剪了6刀,这样,原来的绳子被剪成了多少段?( )
A.40
B.48
C.49
D.56
正确答案:C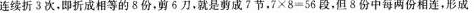

-
第14题:
在桥上用绳子测量桥的高度,把绳子对折垂到水面时尚余8m,把绳子三折垂到水面尚余2m。则桥高和绳长分别为()。A.12m,48mB.10m,36mC.8m,32mD.7m,30m
依题意,绳子长度比桥高的2倍还多:8×2=16(m),绳子长度比桥高的3倍还多:2×3=6(m),所以桥的高度为:16-6=10(m),绳子的长度为:2×l0+16=36(m)。
-
第15题:
一根长200米的绳子对折三次后从中间剪断,最后绳子的段数是( )
A.8
B.9
C.11
D.16
正确答案:B
14.【解析】对折3次后是8根,从中间剪断后多16个头,加上原来绳子的2个头,总计18个头,2个头一个线段,所以有18÷2=9段。故选B。 -
第16题:
有两根绳子,长的比短的长1倍,现在把每根绳子都剪掉6分米,那么长的一根就比短的一根长两倍。长绳子原来的长度是多少分米?( )
 正确答案:B
正确答案:B
设短的长x分米,则长的为(1+1)x分米,列方程得:(1+1)x-6=(x-6)×(1+2),解得x=12,则长绳子为:12×(1+1)=24(分米)。因此本题正确答案为B。 -
第17题:
将一根绳子连续对折3次,然后每隔一定长度剪一刀,并剪了6刀,这样,原来的绳子被剪了多少段?( )
A.40
B.48
C.49
D.56
正确答案:C
连续折3次,即折成相等的8份,剪6刀,就是剪成7节,7×8=56段,但8份中每两份相逢,形成7个“弯”,所以实际上只有56—7=49段。故C正确。 -
第18题:
一根绳子对折三次后,从中剪断,共剪成()段绳子。
A.9
B.6
C.5
D.3
正确答案:A
-
第19题:
一根长200米的绳子对折三次后从中间剪断,最后绳子的段数是( )
A.8 B.9 C.11 D.16
正确答案:B对折3次后是8根,从中间剪断后多16个头,加上原来绳子的2个头,总计18个头,2个头一个线段,所以有18÷2=9段。故选B。
-
第20题:
一根绳子对折三次后,从中剪断,共剪成()段绳子。
A.9 B.6
C.5 D.3答案:A解析:A。此题属于对折绳类题目,利用公式:23+1=9(次)。 -
第21题:
把一根绳子对折, 再对折, 然后把对折后的绳子剪成三段, 这根绳子总共被剪成几小段?( )A.9
B.10
C.11
D.12答案:A解析:剪成三段是剪了两刀,对折了两次,所以 2×2^2+1=9。 -
第22题:
用绳子量桥高,在桥上将绳子4折垂至水面,余3米,把绳剪去6米,3折后,余4米,桥高是多少米?( )。A.36
B.12
C.9
D.7答案:D解析:假设绳长x米,桥高y米,列方程组得:(1)x=4y+3,(2)x-6=3y+4,解得y=7。 -
第23题:
一根绳子对折三次后,从中间剪断,共剪成( )段绳子。
A. 9 B. 6 C. 5 D. 3答案:A解析:本題属于剪绳计数问题。一根绳子连续对折N次,从中剪M刀,则绳子被剪成(2NXM+1)段。代入公式中可得,绳子共剪成23X1 + 1 = 9(段)。故选A。
