将编号1、2、3、4、5的五个小球放入编号为1、2、3、4、5的五个盒子中，每个盒子中只放一个。一共有多少种不同的方法？ A.110 B.115 C.118 D.120

题目
将编号1、2、3、4、5的五个小球放入编号为1、2、3、4、5的五个盒子中，每个盒子中只放一个。一共有多少种不同的方法？

A.110
B.115
C.118
D.120
相似考题

1.：把12个小球放到编号不同的8个盒子里，每个盒子里至少有一个小球，共有（ ）种方法。A．96B．128C．330D．144

2.现在将编号为1、2、3、4、5、6的6个球分别放入编号为1、2、3、4、5、6的6个盒子里，每个盒子放1个球。请问。恰好有2个盒子编号与球编号一样的投放方法有多少种? A．15 B．24 C．135 D．270

3.有16个盒子，里面放了27个小球，每个盒子放了1个、2个或者3个小球，其中放1个小球的盒子数与放2个和3个小球的盒子总数一样多，问：放2个小球的盒子有多少个? A．3 B．4 C．5 D．6

4.把6个标有不同标号的小球放入三个大小不同的盒子里。大号盒子放3个，中号盒子放2个，小号盒子1个，问其有（ ）种放法A. 50B. 60C. 70D. 40

更多“将编号1、2、3、4、5的五个小球放入编号为1、2、3、4、5的五个盒子中，每个盒子中只放一个。一共有多少种不同的方法？ ”相关问题

  • 第1题：

    将四个颜色互不相同的球全部放人编号为1和2的两个盒子里，使得放入每个盒子里球的个数不小于盒子的编号，则不同的放球方法有（ ）种。 A．9 B．10 C．12 D．18


    正确答案：B

  • 第2题：

    A、B、C、D四个盒子中依次放有6、4、5、3个球。第l个小朋友找到放球最少的盒子，从其他盒子中各取一个球放入这个盒子；然后第2个小朋友找到放球最少的盒子，从其他盒子中各取一个球放入这个盒子……如此进行下去。当34位小朋友放完后，问B盒子中放有多少个球?（ ）

    A．4

    B．6

    C．8

    D．11


    正确答案：B

     

  • 第3题：

    将四个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里球的个数不小于盒子的编号，则不同的放球方法有（ ）种。

    A．9

    B．10

    C．12

    D．18


    正确答案：B

  • 第4题：

    有16个盒子。里面放了27个小球，每个盒子放了1个、2个或者3个小球，其中放1个小球的盒子数与放2个和3个小球的盒子总数一样多，问放2个小球的盒子有多少个?

    A．3

    B．4

    C．5

    D．6


    正确答案：C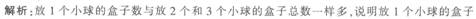



  • 第5题：

    将编号1、2、3、4、5的五个小球放人编号为1、2、3、4、5的五个盒子中，每个盒子中只放 一个。一共有多少种不同的方法？

    A.110
    B.115
    C.118
    D.120

    答案：D
    解析：
    将5个小球进行全排列，即有A55=120种不同的方法。

  • 第6题：

    若将15只相同的球随机放入编号为1,2,3,4的四个盒子中,1号盒可以为空,其余盒子中小球数目不小于盒子编号,则不同的投放方法有（ ）种

    A.56
    B.84
    C.96
    D.108
    E.120

    答案：B
    解析：

  • 第7题：

    若将15只相同的球随机放入编号为1,2,3,4的四个盒子中,每个盒子中小球的数目,不少于盒子的编号,则不同的投放方法有（ ）种

    A.56
    B.84
    C.96
    D.108
    E.120

    答案：A
    解析：
    减少元素法,第一步:先将1,2,3,4四个盒子分别放0,1,2、3个球,因为球是相同的球,故只有一种放法.第二步:余下的9个球放入四个盒子、则毎个盒子至少放一个,使用挡法,即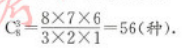

  • 第8题：

    将标号为1，2，3，4，5，6的6张卡片放入3个不同的信封中，若每个信封放2张，其中标号为1，2的卡片放入同一信封，则不同的方法共有（）。

    • A、12种
    • B、18种
    • C、36种
    • D、54种

    正确答案:B

  • 第9题：

    将7个乒乓球放入3个同样的盒子里，允许有的盒子空着不放，共有（）种不同的放法。


    正确答案:8

  • 第10题：

    单选题
    4个不同的小球放入4个不同的盒子里，每个盒子有一个球，有（）种方法。
    A

    4

    B

    10

    C

    12

    D

    24


    正确答案： D
    解析： 此题相当于4个人站成一排共有多少种方法的站排问题，即A（4，4）=24种方法，故选D。

  • 第11题：

    单选题
    现要求将编号为1、2、3、4、5、6的6辆赛车排在编号为1、2、3、4、5、6的6条跑道中，每条跑道只能放一辆车。要求有且只有两辆赛车的编号与其所在跑道的编号相同，共有不同排法的种数是（）。
    A

    9

    B

    80

    C

    135

    D

    184


    正确答案： A
    解析： 根据题意，6辆赛车中两辆编号与其所在跑道的编号相同，有C（2，6）=15种不同情况；余下4辆都不同，即4个元素错位全排，有9种情况。所以，一共有15×9=135种排法。选择C。

  • 第12题：

    单选题
    将标号为1，2，3，4，5，6的6张卡片放入3个不同的信封中，若每个信封放2张，其中标号为1，2的卡片放入同一信封，则不同的方法共有（）。
    A

    12种

    B

    18种

    C

    36种

    D

    54种


    正确答案： B
    解析： 暂无解析

  • 第13题：

    把6个标有不同标号的小球放入三个大小不同的盒子里。大盒子放3个球，中号盒子放2个，小盒子放1个。问共有多少种放法?（　　）A.50  B.60  C.70　　　　D.40


    本题正确答案为B。本题是一个乘法原理与组合综合运用的问题。首先，把球放入盒子需分三步走，这需用乘法原理。其次，放入盒中的球不计顺序，这是一个组合问题，因此，综合以上两点可知，共有C36×C23×C11＝20×3×1＝60种放法

  • 第14题：

    将9个相同的小球放入A、B、C、D四个盒子中，允许有的盒子空着，一共有多少种不同的摆放结果?

    A．220

    B．84

    C．165

    D．120


    正确答案：A
    【答案】A。解析∶在每个盒子中预先放置一个小球，则问题转化为将13个小球放入四个盒子中而且不允许有空着的情况，可以采用隔板法，即在13个球的12个间隔处选择放下3个隔板将其分为4部分，C312=220。

  • 第15题：

    现在将编号为1、2、3、4、5、6的6个球分别放入编号为1、2、3、4、5、6的6个盒子里，每个盒子放1个球。请问，恰好有2个盒子编号与球编号一样的投放方法有多少种?

    A．15

    B．24

    C．135

    D．270


    正确答案：C
    首先选出2个编号和球一样的盒子，有C62＝15种方法；剩余的4个再进行错位重排，有3×3＝9种方法。因此一共有15×9＝135种方法。

  • 第16题：

    从编号a，b，c，d，e的五个小球中任取4个，放在编号为1，2，3，4的盒子里，每个盒里放一个小球，且球b不能放在2号盒中，则不同的放法种数为（）

    A.24种
    B.36种
    C.120种
    D.96种

    答案：D
    解析：

  • 第17题：

    从5个不同的黑球和2个不同的白球中,任选3个球放入3个不同的盒子中,每盒1球,其中至多有1个白球的不同放法共有（ ）种

    A.160
    B.165
    C.172
    D.180
    E.182

    答案：D
    解析：

  • 第18题：

    设有编号为1,2,3,4,5的5个球和编号为1,2,3,4,5的5个盒子,将5个小球放入5个盒子中（每个盒子中放入1个小球）,则至少有2个小球和盒子编号相同的方法有（ ）

    A.36种
    B.49种
    C.31种
    D.28种
    E.72种

    答案：C
    解析：

  • 第19题：

    在编号1,2,3,4的4个盒子中装有绿茶、红茶、花茶和白茶四种茶，每只盒子只装一种茶，每种茶只装一个盒子。已知：（1）装绿茶和红茶的盒子在1,2,3号范围之内；（2）装红茶和花茶的盒子在2,3，4号范围之内；（3）装白茶的盒子在1，2,3号范围之内根据上述，可以得出以下哪项？

    A.绿茶在3号；
    B.花茶在4号；
    C.白茶在3号；
    D.红茶在2号；
    E.绿茶在1号。

    答案：B
    解析：

  • 第20题：

    4个不同的小球放入4个不同的盒子里，每个盒子有一个球，有（）种方法。

    • A、4
    • B、10
    • C、12
    • D、24

    正确答案:D

  • 第21题：

    将10个小球随机放入甲、乙、丙三个盒子中，且每个盒子中小球的个数均为质数，接着在甲、乙、丙三个盒子中分别放入等于其盒内球数的2、3、4倍的小球。两次共放入了39个小球。最终甲盒中的小球比乙盒（）

    • A、多2个
    • B、少11个
    • C、少2个
    • D、少20个

    正确答案:B

  • 第22题：

    单选题
    将10个小球随机放入甲、乙、丙三个盒子中，且每个盒子中小球的个数均为质数，接着在甲、乙、丙三个盒子中分别放入等于其盒内球数的2、3、4倍的小球。两次共放入了39个小球。最终甲盒中的小球比乙盒（）
    A

    多2个

    B

    少11个

    C

    少2个

    D

    少20个


    正确答案： C
    解析： 不定方程问题。设甲、乙、丙三个盒子中第一次放入小球的个数分别为x、y、z个，由题意列方程得：x+y+z=10，2x+3y+4z=29；消去z后可得：2x+y=11，由于x、y均为质数，易得x=3，y=5，z=2。（x=2，y=7时，z=1，不满足质数的要求。）最后将甲、乙、丙盒子中小球个数代入计算即可。因此，本题答案为B选项。

  • 第23题：

    单选题
    将20个相同的小球放入编号分别为1，2，3，4的四个盒子中，要求每个盒子中的球数不少于它的编号数，则共有多少种放法？
    A

    340

    B

    286

    C

    446

    D

    364


    正确答案： A
    解析：

相关内容