连接正四面体侧棱的中点和底面的中心A、E、F、G、H构成多面体（如右图所示）。问该多面体与正四面体的体积比是多少？（ ） A. 1 : 8 B. 1 : 6 C. 1：4 D. 1 : 2

题目
连接正四面体侧棱的中点和底面的中心A、E、F、G、H构成多面体

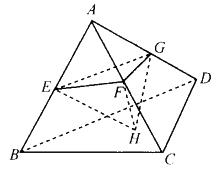
（如右图所示）。问该多面体与正四面体的体积比是多少？（ ）

A. 1 : 8
B. 1 : 6
C. 1：4
D. 1 : 2
相似考题

1.下列属于不规则单元的有()。A.正四面体单元B.正三棱体单元C.任意四面体单元D.正六面体单元

2.不属于规则单元的是( ) 。A.正四面体单元B.正三棱体单元C.正六面体单元D.曲边单元

3.正四面体的棱长增长10％，则表面积增加（ ）A．21％B．15％C．44％D．40％

4.属于不规则单元的有( )。A、正四面体单元B、正三棱体单元C、任意曲边单元D、任意六面体单元

更多“连接正四面体侧棱的中点和底面的中心A、E、F、G、H构成多面体 ”相关问题

  • 第1题：

    一个系统的模块结构图如下所示，用{×，×，×}表示这个系统的测试模块组合。下面的选项中(71)表示自顶向下的测试，(72)表示三明治式测试。

    A．{A){A,B,C,D,E}{A，B，C，D，E，F，G，H，I，J，K}

    B．{F}{G){H}{I}{J}{K}{B，F，G}{C,H}{D,I,J}{E,K}{A，B，C，D，E，F，G，H，I，J，K}

    C．{K}{J}{I}{H}{G}{F}{B}{C}{D}{E}{A，B，C，D，E，F，G，H，I，J，K}

    D．{A}{F}{G}{H}{I}{J}{K}{B，F，G}{C,H}{D,I,J}{E,K}{A，B，C，D，E，F，G，H，I，J，K}


    正确答案：A

  • 第2题：

    如图，正四面体P-ABC的棱长为a，D、E、F分别为PA、PB、PC的中点，G、H、M 分别为DE，EF，FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为（ ）。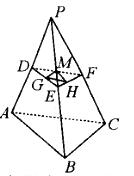


    A. 1 : 8
    B. 1 : 16
    C. 1 : 32
    D. 1 : 64

    答案：D
    解析：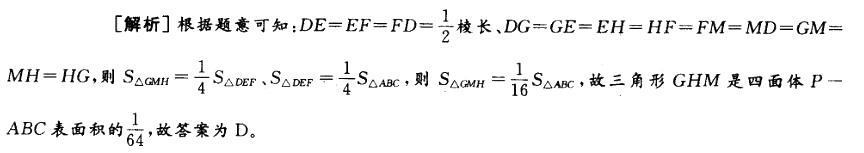

  • 第3题：

    如图，正四面体P-ABC的棱长为a，D、E、F分别为棱PA、PB、PC的中点，G、H、M分别为DE、EF、FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为：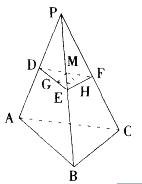


    A.1：8
    B.1：16
    C.1：32
    D.1：64

    答案：D
    解析：
    DE=AB/2=a/2，同理三角形GHM的边长为DE/2=a/4。所以三角形GHM和三角形ABC的面积比为边长比的平方1：16。正四面体P-ABC的表面积是三角形ABC面积的4倍，故所求比例为1：16x4=1：64。

  • 第4题：

    连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米，问正八面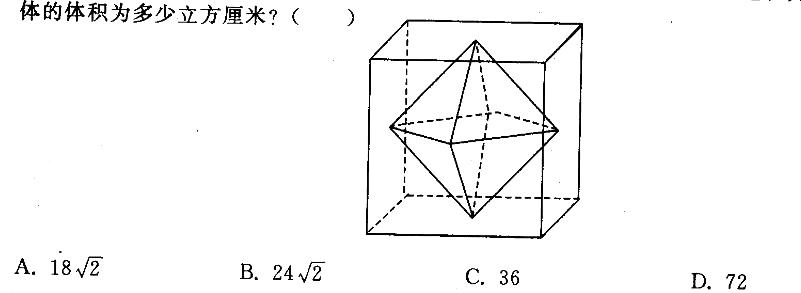


    答案：C
    解析：
    该正八面体可以看做由两个四棱锥拼成的，每个四棱锥的底面为原正方体四个侧面的中心连线，高分别为上下两个正方体底面中心到四棱锥底面的距离，解得V= 1/3x(62x1/2)X3X2 =36(cm3)。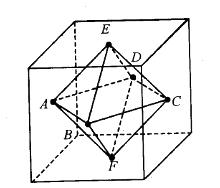

  • 第5题：

    读城市中心与郊区垂直(H)方向上的气压(P)分布图。完成题。



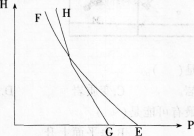
    根据热力环流的原理，城郊之间正确的环流方向是（　　）。查看材料

    A．E→F→H→G→E
    B．E→G→H→F→E
    C．G→E→F→H→G
    D．G→E→H→F→G

    答案：B
    解析：
    城市中心区为热岛，温度高，气流上升，近地面为低压，高空形成高压，所以垂直方向上气压差异小；郊区气温低，近地面形成高压，高空形成低压，所以垂直方向上气压差别大，所以C为市中心近地面．E为郊区近地面．热力环流的流向为E→G→H→F→E。所以本题选择B选项。

  • 第6题：

    棱长为3的正四面体，以其3个侧面的重心为顶点的三角形面积为：


    答案：A
    解析：
    正四面伴的侧面是等边三角形，其重心为各边中线的交点。如左图可知，重心O将中线

  • 第7题：

    棱柱体由（）构成。

    • A、底面
    • B、底边
    • C、侧棱
    • D、侧面
    • E、底圆

    正确答案:A,B,C,D

  • 第8题：

    韶山4改型电力机车司机室外形制成的多平面的（）多面体。

    • A、锥形
    • B、梯形
    • C、方形
    • D、棱形

    正确答案:D

  • 第9题：

    简单多面体的顶点数V、面数F及棱数E间有关系V+F-E=2这个公式叫（）。

    • A、笛卡尔公式
    • B、牛顿公式
    • C、莱布尼茨公式
    • D、欧拉公式

    正确答案:D

  • 第10题：

    单选题
    配位多面体相联的最稳定形式是（）
    A

    共面连接

    B

    共角顶连接

    C

    共棱连接


    正确答案： A
    解析： 暂无解析

  • 第11题：

    多选题
    棱柱体由（）构成。
    A

    底面

    B

    底边

    C

    侧棱

    D

    侧面

    E

    底圆


    正确答案： E,A
    解析： 暂无解析

  • 第12题：

    单选题
    简单多面体的顶点数V、面数F及棱数E间有关系V+F-E=2这个公式叫（）。
    A

    笛卡尔公式

    B

    牛顿公式

    C

    莱布尼茨公式

    D

    欧拉公式


    正确答案： A
    解析： 暂无解析

  • 第13题：

    如右图，正四面体P-ABC的棱长为口，D、E、F分别为棱PA、PB、PC的中点，G、H、M分别为DE、EF、FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为：

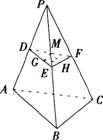
    A.1：8

    B.1：16

    C.1：32

    D.1：64


    正确答案：D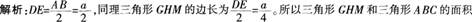
    比为边长比的平方1：16。正四面体P－ABC的表面积是三角形ABC面积的4倍，故所求比例为1：(16×4)＝1：64。

  • 第14题：

    将棱长为1的正方体的六个面的中点相连接可以得到一个八面体，则这个八面体的体积为：


    答案：A
    解析：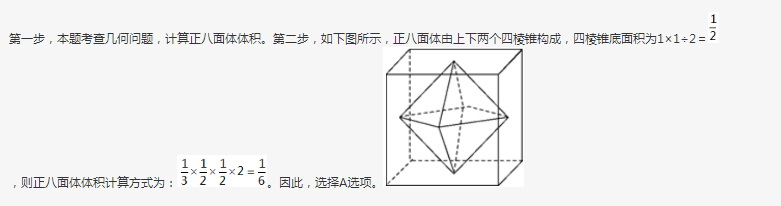

  • 第15题：

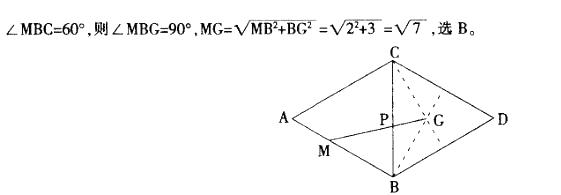
    如图，A-BCD是棱长为3的正四面体，M是棱AB上的一点，且MB=2MA，G是三角形


    答案：B
    解析：
    将面ABC和面BCD展开至一个平面，如图所示，连接BG、CG。要使MP+PG最小，则P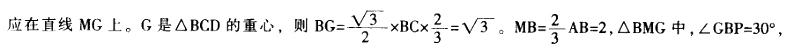

  • 第16题：

    正三棱柱ABC—A/B/C/，底面边长为a，侧棱长为h．
    (I)求点A到△A/BC所在平面的距离d；
    (Ⅱ)在满足d=1的上述正三棱柱中，求侧面积的最小值．


    答案：
    解析：

  • 第17题：

    如，正方体ABCD-A′B′C′D′的棱长为2,F是棱C′D′的中点，则AF的长为


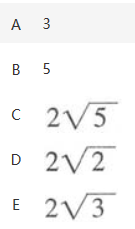    答案：A
    解析：

  • 第18题：

    已知正六棱锥底面的边长为2cm，侧棱长4cm求正六棱锥的体积？

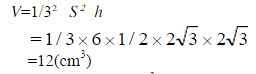
    略

  • 第19题：

    简单多面体的顶点数V、面数F及棱数E间有关系V+F-E=2。这个公式的发现者是（）


    正确答案:莱昂哈德欧拉

  • 第20题：

    二次对称轴出现的位置一般是（）

    • A、相对棱的中点
    • B、两底面中心
    • C、一条棱与相对底面的中心
    • D、相对两柱面的中心

    正确答案:A,B,C,D

  • 第21题：

    甲烷分子为正四面体结构，其中碳原了位于正四面体的中心，四个氢原子位于四面体的四个顶点。


    正确答案:正确

  • 第22题：

    单选题
    有关系模式P（A，B，C，D，E，F，G，H，I，J），根据语义有如下函数依赖集：F={ABD→E，AB→G，B→F，C→J，C→I，G→H）。现将关系模式P分解为两个关系模式P1（A，B，D，E，F，G，H）和P2（C，I，J）。这个分解（）。
    A

    不具有无损连接性，不保持函数依赖

    B

    具有无损连接性，不保持函数依赖

    C

    不具有无损连接性，保持函数依赖

    D

    具有无损连接性且保持函数依赖


    正确答案： C
    解析： 暂无解析

  • 第23题：

    多选题
    二次对称轴出现的位置一般是（）
    A

    相对棱的中点

    B

    两底面中心

    C

    一条棱与相对底面的中心

    D

    相对两柱面的中心


    正确答案： B,D
    解析： 暂无解析

相关内容