晚上21点整，甲乙两车同时从A地出发匀速开往B地，同一时间丙丁两车从B地出发匀速开往A地，甲车时速是乙车的3倍，乙车行驶3小时后首先与丙相遇，再行驶1小时之后与丁相遇，若4辆车到达目的地的时间正好都是第二天内的整点时同，问甲车和丙车是在几点相遇的（）A、0点整 B、23点30分 C、23点整 D、22点30分

题目
晚上21点整，甲乙两车同时从A地出发匀速开往B地，同一时间丙丁两车从B地出发匀速开往A地，甲车时速是乙车的3倍，乙车行驶3小时后首先与丙相遇，再行驶1小时之后与丁相遇，若4辆车到达目的地的时间正好都是第二天内的整点时同，问甲车和丙车是在几点相遇的（）

A、0点整
B、23点30分
C、23点整
D、22点30分
相似考题

1.甲车从A地，乙车和丙车从8地同时出发，相向而行。已知甲车每小时行65公里，乙车每小时行73公里，丙车每小时行55公里。甲车和乙车相遇后，经过15小时又与丙车相遇，那么A、B两地相距（ ）公里。A．10100B．13800C．10600D．14800

2.甲、乙两车同时从A、B两地出发，相向而行。甲到达B地后立即返回，回到A地后又立即向B地行驶；乙到达A地后立即返回，回到B地后又立即向A地行驶。两车如此往复，行驶速度不变。若两车第2次迎面相遇距B地20千米，第3次迎面相遇距离A地10千米，问A、B两地的距离是多少千米？（ ）A.20B.30C.40D.70

3.A、B两地相距540千米。甲、乙两车同时从A地出发，往返行驶于A、B两地之间，都是到达之后立即返回，乙车较甲车快。设两辆车同时从A地出发后第一次和第二次相遇都在途中P地。那么到两车第三次相遇为止，乙车共走了多少千米？A．1080B．1620C．1890D．2160

4.：甲、乙两车同时从A地出发开往B地。甲车到达8地后立即返回，在离B地45千米处与乙车相遇，甲、乙两车的速度比是3：2。求A，B两地的路程是多少千米？（ ）A．220B．200C．225D．250

参考答案和解析
答案：C
解析：
本题考查相遇追及问题。乙车行驶3小时后与丙相遇，再行驶1小时后与丁相遇，根据相遇问题公式可得：

{图}
{图1}

四辆车均在第二天整点到达，则甲乙丙丁四车的速度应均可被路程整除，且所用时间应不小于3小时，所设情况满足情形。则甲丙两车相遇需要12/（3+3）=2小时，从晚上21点出发，相遇时应为21+2=23点。故本题答案为C选项。
【知识点】相遇追及
更多“晚上21点整，甲乙两车同时从A地出发匀速开往B地，同一时间丙丁两车从B地出发匀速开往A地，甲车时速是乙车的3倍，乙车行驶3小时后首先与丙相遇，再行驶1小时之后与丁相遇，若4辆车到达目的地的时间正好都是第二天内的整点时同，问甲车和丙车是在几点相遇的（）”相关问题

  • 第1题：

    甲、乙两车分别从A、B两地同时出发，相向而行，10小时后两车相遇，此时甲车比乙车多行了100千米，8小时后，甲到达B地，若乙车每小时行驶40千米，问乙再过多长时间到达A地?

    A．3小时

    B．3.5小时

    C．4小时

    D．4.5小时


    正确答案：D
    [答案] D[解析]甲车每小时比乙车多行驶100+10=10千米，甲车经过10+8=18小时到达，此时比乙车多行驶180千米，乙车再经过180+40=4.5小时到达A地。

  • 第2题：

    甲、乙两辆旅游车同时从A、B两地出发，相向而行，4小时相遇。相遇后甲车继续行驶了3小时到达8地，乙车每小时行24千米。问：A、B两地相距多少千米?（ ）

    A．96

    B．106

    C．144

    D．224


    正确答案：D

  • 第3题：

    甲车从A地、乙车从B地同时出发匀速相向行驶，第一次相遇距A地100千米，两车继续前进到达对方起点后立即以原速度返回，在距离A地80千米的位置第二次相遇，则AB两地相距多少千米？

    A.170
    B.180
    C.190
    D.200

    答案：C
    解析：
    第一步，本题考查行程问题，属于相遇追及类，用比例法解题。
    第二步，设AB两地相距S千米，根据第一次相遇距A地100千米，可知甲车走了100，两人共走S；由第二次相遇距A地80千米，可知甲车从出发到第二次相遇走了2S－80，两人共走3S。

  • 第4题：

    甲车从A地，乙车和丙车从B地同时出发，相向而行。已知甲车每小时行65公里，乙车每小时行73公里，丙车每小时行55公里。甲车和乙车相遇后，经过15小时又与丙车相遇， 那么A、B两地相距（ ）公里。
    A. 10100 B. 13800 C. 10600 D. 14800


    答案：B
    解析：
    设从出发到曱乙相遇经过了 t小时，三车行驶情况如下图所示：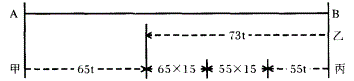

    根据题意可列方程：65X 15 + 55X 15十55t=73t，解得t=100;A、B两地的距离应为：65X 100 + 73X100 = 13800(公里）。答案为 B。

  • 第5题：

    甲、乙两车分别以30公里/小时和40公里/小时的速度同时匀速从A地开往B地，丙车以50公里/小时的速度匀速从B地开往A地。A、B两地距离120公里。问丙车遇到乙车后多久会遇到甲车？

    A.8分钟
    B.10分钟
    C.12分钟
    D.15分钟

    答案：B
    解析：

  • 第6题：

    甲车上午8点从A地出发匀速开往B地，出发30分钟后乙车从A地出发以甲车2倍的速度前往B地，并在距离B地10千米时追上甲车。如乙车9点10分到达B地，问甲车的速度为多少千米/小时？

    A.30
    B.36
    C.45
    D.60

    答案：A
    解析：
    解法一：第一步，本题考查行程问题中的追及问题。
    第二步，从题目中可知乙车的速度是甲车的两倍，即甲乙速度之比为1∶2，在路程一定时，速度与时间呈反比，距离B市10公里时乙追上甲，甲比乙多走30分钟，最后总路程相等，则甲走了60分钟，乙走了30分钟。则乙再行驶40-30=10分钟到达了B市，则这一段路程甲需要20分钟=



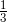
    小时，可知甲的速度=



    =30（千米/小时）。
    因此，选择A选项。
    解法二：可以利用选项相关进行秒杀，乙的速度是甲的两倍，选项A与D存在两倍关系，正确选项来自二者之中，所求量为甲的速度，选小的。
    因此，选择A选项。

  • 第7题：

    甲、乙两列直达高铁同时从C、D两站出发，匀速相向而行，两车相遇时甲车比乙车多行驶120千米，相遇后甲车经过96分钟到达D站，乙车经过150分钟到达C站。问C、D两站相距多少千米？

    A.400
    B.450
    C.540
    D.1080

    答案：D
    解析：

  • 第8题：

    单选题
    甲车上午8点从A地出发匀速开往B地，出发30分钟后乙车从A地出发以甲车2倍的速度前往B地，并在距离B地10千米时追上甲车。如乙车9点10分到达B地，问甲车的速度为多少千米/小时？（　　）
    A

    30

    B

    36

    C

    45

    D

    60


    正确答案： D
    解析：
    根据题意可知，设甲车的速度为X千米/小时，乙车的速度为甲车的2倍即2X千米/小时。甲车出发30分钟即1/2小时后乙车开始追，则两车的路程差为X/2千米，由追及公式“路程差＝速度差×追及时间”可得，追及时间＝路程差/速度差＝（X/2）÷（2X－X）＝1/2（小时），所以乙从出发到追上甲共花费1/2小时。乙车在上午8点的30分钟后出发，9点10分到达B地，共用时40分钟，也就是2/3小时。设乙在C点追上甲，则CB＝10千米，乙车从C地到B地用时2/3－1/2＝1/6（小时）。则乙车的速度＝10千米/（1/6）小时＝60（千米/小时），甲车的速度＝60÷2＝30（千米/小时）。因此答案选A。

  • 第9题：

    单选题
    甲车从A地、乙车和丙车从B地同时出发，相向而行。已知甲车每小时行65千米，乙车每小时行73千米，丙车每小时行55千米。甲车和乙车相遇后，经过15小时又与丙车相遇，那么A、B两地相距（　　）千米。
    A

    10100

    B

    13800

    C

    10600

    D

    14800


    正确答案： A
    解析：
    设从出发到甲、乙相遇经过了t小时，三车行驶情况如下图所示：即65×15＋55×15＋55t＝73t，解得t＝100；则A、B两地的距离应为65×100＋73×100＝13800千米。

  • 第10题：

    甲车从A地，乙车和丙车从B地同时出发，相向而行。已知甲车每小时行65公里，乙车每小时行73公里，丙车每小时行55公里。甲车和乙车相遇后，经过15小时又与丙车相遇，那么A、B两地相距（ ）公里。

    A．10100

    B．13800

    C．10600

    D．14800


    正确答案：B
    设从出发到甲乙相遇经过了t小时，三车行驶情况如下图所示：

    根据题意可列方程：65×15+55×15+55t=73t，解得t=100(小时)；A、B两地的距离应为：65×100+73×100=13800(公里)。答案为B。

  • 第11题：

    甲、乙两车分别从P、Q两地同时出发，相向而行。相遇时，甲车比乙车多行驶36千米，乙车所行驶路程为甲车所行驶路程的4/7，则P，Q两地相距（ ）千米。

    A. 72
    B. 96
    C. 112
    D. 132

    答案：D
    解析：
    甲：乙=7:4，总路程是11的倍数，本题选择D。

  • 第12题：

    甲、乙二人分别从A、B两地驾车同时出发，匀速相向而行，甲车的速度是乙车的2/3，两车开出6小时后相遇，相遇后以原速继续前进。问甲比乙晚几个小时到达目的地？

    A. 2
    B. 3
    C. 4
    D. 5

    答案：D
    解析：
    甲乙二人的速度比是2:3，所以时间比就是3:2，根据时间的比例，甲剩下的路程所需时间是9h，乙剩下的路程时间是4h，二者加上原来的时间就是15h和10h，所以选择D。

  • 第13题：

    A、B两地相距540千米。甲、乙两车同时从4地出发，往返行驶于4、B两地之间，都是到达之后立即返回，乙车较甲车快。设两辆车同时从4地出发后第一次和第二次相遇都在途中P地。那么到两车第三次相遇为止，乙车共走了多少千米？

    A.1080
    B.1620
    C.1890
    D.2160

    答案：D
    解析：
    第一次相遇，甲、乙共走了2个全程；第二次相遇，甲、乙共走了4个全程，故从第一次 相遇到第二次相遇时，甲所走的路程等于它从出发到第一次相遇所走的路程，即(如图所示），故甲、乙 两车的速度比为1:2。两车第三次相遇时，甲、乙共走了 6个全程，其中乙走了 6÷（2+1）×2=4个全程，即540×4=2160千米。

  • 第14题：

    甲乙两车分别从A、B两地匀速相向而行，甲乙两车在途中某地相遇，此时甲车比乙车多行驶了18千米，相遇后至终点甲车一共走了4. 5小时，乙车比甲车多用了3.5小时，则AB两地的距离为（ ）千米。

    A. 63
    B. 126
    C. 65
    D. 130

    答案：B
    解析：

  • 第15题：

    丙地为甲、乙两地之间高速公路上的一个测速点，其与甲地之间的距离是与乙地之间距离的一半，A、B两车分别丛甲地和乙地同时出发匀速相向而行，第一次迎面相遇的位置距离丙地500米，两车到达对方出发地后立刻原路返回，第二次两车相遇也为迎面相遇，问第二次相遇的位置一定：

    A.距离甲地1500米
    B.距离乙地1500米
    C.距离丙地1500米
    D.距离乙、丙中点1500米

    答案：B
    解析：
    第一步，本题考查行程问题。
    第二步，设甲丙的距离为x米，那么乙丙的距离为2x米，第二次仍为迎面相遇，故两车速度比不能超过2∶1，那么第一次相遇A车走了（x＋500）米，B车走了（2x－500）米，根据两端出发多次相遇问题公式，第二次相遇走的路程是第一次的3倍，故第二次相遇时A车共走了3×（x＋500）＝3x＋1500（米），3x是甲乙的全程，故A车走了从甲到乙的全程后又走了1500米，即距离乙地1500米。
    因此，选择B选项。

  • 第16题：

    单选题
    甲乙两车分别从A、B两地匀速相向而行，甲乙两车在途中某地相遇，此时甲车比乙车多行驶了18千米，相遇后至终点甲车一共走了4.5小时，乙车比甲车多用了3.5小时，则A、B两地的距离为（　　）千米。
    A

    63

    B

    126

    C

    65

    D

    130


    正确答案： C
    解析：
    设甲车速度为x千米/小时，乙车速度为y千米/小时，AB两地的距离为2s千米，由题意可列方程得（s＋9）/y＝4.5＋3.5①，（s－9）/x＝4.5②，（s＋9）/x＝（s－9）/y③，由②÷①得（s－9）/（s＋9）＝9x/16y④，由③得（s＋9）/（s－9）＝x/y⑤，由④÷⑤得[（s－9）/（s＋9）]2＝9/16，即（s－9）/（s＋9）＝3/4，解得s＝63，所以AB全程距离为126千米。

  • 第17题：

    单选题
    A、B两地相距540千米。甲、乙两车往返行驶于A、B两地之间，都是到达一地之后立即返回，乙车较甲车快。设两辆车同时从A地出发后第一次和第二次相遇都在途中P地。那么两车第三次相遇为止，乙车共走了多少千米？（）
    A

    120

    B

    1440

    C

    2160

    D

    2880


    正确答案： D
    解析： 暂无解析

  • 第18题：

    单选题
    甲车从A地，乙车从B地同时出发匀速相向行驶，第一次相遇距离A地100千米。两车继续前进到达对方起点后立即以原速度返回，在距离A地80千米的位置第二次相遇。则AB两地相距多少千米？
    A

    170

    B

    180

    C

    190

    D

    200


    正确答案： D
    解析：

相关内容