设X是正态变量,均值为0,标准差为2,则X的绝对值小于2的概率约为()。A.5%B.70%C.90%D.95%

题目
设X是正态变量,均值为0,标准差为2,则X的绝对值小于2的概率约为()。

A.5%

B.70%

C.90%

D.95%

相似考题

1.设某厂生产电阻器的阻值X～N(60.5，1.22)，已知该厂电阻器阻值的规范界限为60±2，则超过上限的概率可表示为( )。. 设X～N(μ，σ2)，σ未知，从中抽取n＝16的样本，其样本均值为x，样本标准差为s，则总体均值μ的置信度为95%的置信区间为( )。A． [*]

2.正态随机变量x的观测值落在距均值的距离为2倍标准差范围内的概率约为（ ）。A．68%B．95%C．32%D．50%

3.正态随机变量X的观测值落在距均值的距离为2倍标准差范围内的概率约为（ ）。 A．50% B．68% C．95% D．99%

4.正态随机变量X的观测值落在距均值的距离为2倍标准差范围内的概率约为( )。A．68%B．95%C．32%D．50%

参考答案和解析
参考答案：B
更多“设X是正态变量,均值为0,标准差为2,则X的绝对值小于2的概率约为()。 ”相关问题

  • 第1题：

    正态随机变量X的观测值落在距均值的距离为2倍标准差范围内的概率约为（ ）。

    A．68%

    B．95%

    C．32%

    D．50%


    正确答案：B
    1倍标准差内对应的概率68％，2倍标准差内对应的概率为95％，3倍标准差对应的概率为99％。故选B。

  • 第2题：

    设X～U(0，2)，则Y—X2在(0，4)内的概率分布密度为( )。



    答案：A
    解析：
    因为x在(0，2)中变化时，y=x2为单调函数，从而可直接用公式得解

  • 第3题：

    设X～N（0,1），则X≥2的概率为（）。

    A．0.9772

    B．0.5

    C．0.1587

    D．0.02275


    自于 故 于是得p的矩估计 虽然总体分布中只含有一个未知参数，但若运用总体的一阶矩将解不出未知参数矩估计的显函数形式．应再求其二阶矩，二者相结合便可以得到参数矩估计的显函数形式

  • 第4题：

    设随机变量X～U［1,7］,则方程x^2+2Xx+9=0有实根的概率为().



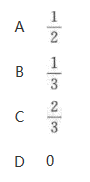    答案：C
    解析：
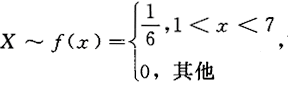    ，方程x^2+2Xx+9=0有实根的充要条件为.

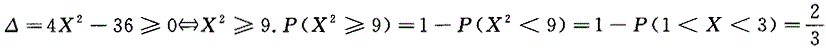
  • 第5题：

    设随机变量X～N（μ,σ^2）,且方程x^2+4r+X=0无实根的概率为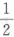,则μ=_______.


    答案：1、4
    解析：
    因为方程x^2+4x+X=0无实根，所以16-4X小于0，即X>4.由X～N（μ，σ）且P(X>4)=1/2 得μ=4

相关内容