某二叉树的前序遍历序列为abdgcefh,中序遍历序列为dgbaechf,则其后序遍历序列为()。AbdgecefhaBgdbecfhaCbdgaechfDgdbehfca
题目
某二叉树的前序遍历序列为abdgcefh,中序遍历序列为dgbaechf,则其后序遍历序列为()。
Abdgecefha
Bgdbecfha
Cbdgaechf
Dgdbehfca
相似考题
更多“某二叉树的前序遍历序列为abdgcefh,中序遍历序列为dgbaechf,则其后序遍历序列为()。 ”相关问题
-
第1题:
一棵二叉树的中序遍历序列为DBGEUJOCIF,后序遍历序列为DCJHEBIPCO,则其前序遍历序列为(87)。
A.OBCDEFGHIJ
B.OBDEGHJCFI
C.OBDEGHJPIC
D.OBDECJHCFI
正确答案:B
解析:我们知道后序遍历序列最后一个节点是根结点,所以该二叉树根节点为O;又因为前序遍历序列中,左子树在根结点前面;右子树在根结点后面,所以O,前面的部分为其左子树,后面的部分为右子树。对得到的左子树和右子树用同样的方法继续进行划分,直至子树只剩一个结点,此时可以得到树的结构,于是可得到它的前序遍历序列。 -
第2题:
某二叉树的前序遍历序列为UKLMNO,中序遍历序列为JLKINMO,则后序遍历序列为()。A.JLKMNOI
B.LKNJOMI
C.LKJNOMI
D.LKNoMI答案:C解析: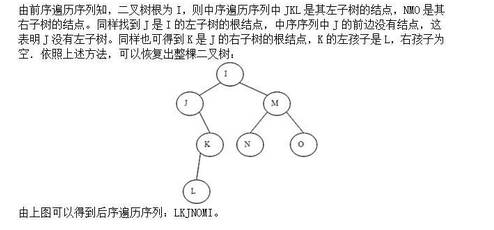
-
第3题:
已知某二叉树的先序遍历序列为CEDBA,中序遍历序列为DEBAC,则它的后序遍历序列为()。
A.DABEC
B.ACBED
C.DEABC
D.DECAB
dabec -
第4题:
假设一棵二叉树的后序遍历序列为DGJHEBIFCA,中序遍历序列为DBGEHJACIF,则其前序遍历序列为______。
A.ABCDEFGHIJ
B.ABDEGHJCFI
C.ABDEGHJFIC
D.ABDEGJHCFI
正确答案:B
解析:这类题目,可以根据所给条件,还原二叉树,然后再进行前序遍历。还原二叉树的要点是首先确定根结点,再确定左子树的组成结点和右子树的组成结点。然后再针对每个左子树和右子树,继续确定其根结点以及左右子树。重点是,根据后序遍历的特点是,最后一个结点必然为根。中序遍历中,根结点的左边,是左子树的结点,右边是右子树的结点。分析过程如下:①首先,根据后序遍历为DGJHEBIFCA,说明这棵二叉树的根为A。再根据中序遍历的结果:DBGEHJACIF,说明DBGEHJ在根结点A的左边,为左子树上的结点。CIF在根结点A的右边,是右子树上的结点。如图8-25所示。②根据后序遍历结果,DGJHEBIFCA,说明CIF这棵子树上,C是根结点。再根据IF在中序遍历中的位置,可知FI都是其右子树。再根据后序遍历结果,可知,F为根,I是其右结点。如图8-26所示。③对于DBGEHJ这棵左子树,根据后序遍历结果可知,B是其根结点。再根据中序遍历结果可知,D是其左子树,GEHJ是其右子树。如图8-27所示。④对于GEHJ这个二叉树,根据后序遍历结果,E为根结点。再根据中序遍历结果,HJ为其右子树。G为其左子树。如图8-28所示。⑤对于HJ,根据后序遍历结果,H是根,再根据中序遍历结果,J是H的右子树。构成二叉树如图8-29所示。对此二叉树进行前序遍历的结果是:ABDEGHJCFI。选项B为本题正确答案。 -
第5题:
某二叉树的前序遍历序列为ABDGCEFH,中序遍历序列为DGBAECHF,则后序遍历序列为()。
A.BDGCEFHA
B.GDBECFHA
C.BDGAECHF
D.GDBEHFCA
A
