对变量进行计算处理时,先求出一系列观察值与其平均值的离差平方和,再除以观察次数减1的值,最后求这个值的平方根,这样得出的数值称作()A、全距B、标准差C、算术平均值D、众数

题目
对变量进行计算处理时,先求出一系列观察值与其平均值的离差平方和,再除以观察次数减1的值,最后求这个值的平方根,这样得出的数值称作()

A、全距

B、标准差

C、算术平均值

D、众数

相似考题

1.用最小二乘法以利润率为因变量拟合直线回归方程，其最小二乘法的原理是使（ ）。A．实际Y值与理论 值的离差和最小B．实际Y值与理论 值的离差平方和最小C．实际Y值与Y平均值的离差和最小D．实际Y值与Y平均值的离差平方和最小

2.最小平方的中心思想,使通过数学模型,配合一条较为理想的趋势线。这条趋势线必须满足()。A.原数列的观察值与模型的估计值的离差平方和为零B.原数列的观察值与模型的估计值的离差平方和为最小C.原数列的观察值与模型的估计值的离差总和为零D.原数列的观察值与模型的估计值的离差总和为最小

3.用最小平方配合直线趋势要求()。A.观察值与趋势值之间的离差平方和等于零B.观察值与趋势值的离差平方和为最小C.观察值与趋势值之间的离差平方和为最小D.观察值与趋势值之间的离差平方和为1

4.对数据进行计量时将某个变量所有观察到的不同值加总再除以观察次数所得的值是()A、全距B、中位数C、算术平均值D、众数

更多“对变量进行计算处理时,先求出一系列观察值与其平均值的离差平方和,再除以观察次数减1的值,最后求这个值的平方根,这样得出的数值称作() ”相关问题

  • 第1题：

    用最小二乘法以利润率为因变量拟合直线回归方程，其最小二乘法的原理是使( )。

    A．实际Y值与理论Y值的离差和最小

    B．实际Y值与理论Y值的离差平方和最小

    C．实际Y值与Y平均值的离差和最小

    D．实际Y值与Y平均值的离差平方和最小


    正确答案：B
    解析：最小二乘法估计回归方程中参数的原理是：每一个指标实测值与指标理论值的离差平方和最小，即Q(β0，β1)=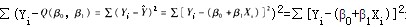最小。

  • 第2题：

    最小二乘法的原理是使得（ ）最小。

    A.因变量的观测值Yi与自变量的观测值Xi之间的离差平方和
    B.因变量的观测值Yi与估计值之间的离差平方和
    C.自变量的观测值Xi与均值之间的离差平方和
    D.因变量的观测值Yi与均值之间的离差平方和

    答案：B
    解析：
    【知识点】 最小二乘法；
    最小二乘法就是使因变量的观测值Yi与估计值之间的离差（又称残差）平方和最小来估计参数和的方法。

  • 第3题：

    回归平方和是指

    A．被解释变量的观测值与其均值的离差平方和

    B．被解释变量的回归值与其均值的离差平方和

    C．被解释变量的总离差平方和与残差平方和之差

    D．解释变量变动所引起的被解释变量的变动的大小


    被解释变量的回归值 与其均值 的离差平方和;被解释变量的总离差平方和 与残差平方和 之差;解释变量变动所引起的被解释变量的变动的大小

  • 第4题：

    样本方差与随机变量数字特征中的方差的定义不同在于()。

    A:是由各观测值到均值距离的平方和除以样本量加1，而不是直接除以样本量
    B:是由各观测值到均值距离的平方和除以样本量减1，而不是直接除以样本量
    C:是由各观测值到均值距离的平方和除以样本量，而不是直接除以样本量加1
    D:是由各观测值到均值距离的平方和除以样本量，而不是直接除以样本量减1

    答案：B
    解析：

  • 第5题：

    用最小平方配合直线趋势要求（）

    A观察值与趋势值之间的离差平方和等于零；

    B观察值与趋势值的离差平方和为最小；

    C观察值与趋势值之间的离差平方和为最小；

    D观察值与趋势值之间的离差平方和为1；


    C
    略

相关内容