设函数f(x)在x=0处连续,下列命题错误的是( ).
题目
设函数f(x)在x=0处连续,下列命题错误的是( ).
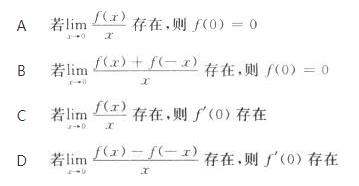
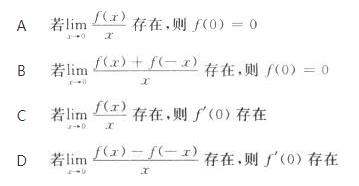
相似考题
参考答案和解析
答案:D
解析:

更多“设函数f(x)在x=0处连续,下列命题错误的是( ). ”相关问题
-
第1题:
设f(x)是定义在[-a,a]上的任意函数,则下列答案中哪个函数不是偶函数?A.f(x)+f(-x)
B.f(x)*f(-x)
C.[f(x)]2
D.f(x2)答案:C解析:提示:利用函数的奇偶性定义来判定。选项A、B、D均满足定义F(-x)=F(x),所以为偶函数,而C不满足,设F(x)= [f(x)]2,F(-x)= [f(-x)]2,因为f(x)是定义在 [-a,a]上的任意函数,f(x)可以是奇函数,也可以是偶函数,也可以是非奇非偶函数,从而推不出F(-x)=F(x)或 F(-x) = -F(x)。 -
第2题:
设函数f(x)在区间[a,b]上连续,则下列结论中哪个不正确? 答案:A解析:
答案:A解析:
-
第3题:
设F(x)是连续函数f(x)的一个原函数,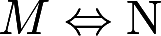 表示“M的充分必要条件是N”,则必有
表示“M的充分必要条件是N”,则必有
AF(x)是偶函数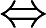 f(x)是奇函数
f(x)是奇函数
BF(x)是奇函数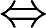 f(x)是偶函数
f(x)是偶函数
CF(x)是周期函数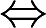 f(x)是周期函数
f(x)是周期函数
DF(x)是单调函数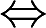 f(x)是单调函数答案:A解析:
f(x)是单调函数答案:A解析:
-
第4题:
设函数f(x)连续,则下列函数中必为偶函数的是( )
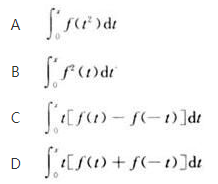 答案:D解析:
答案:D解析: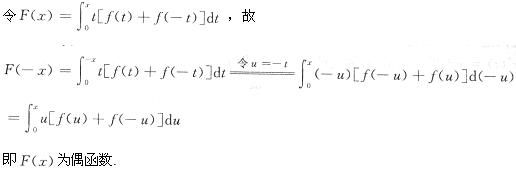
-
第5题:
设F(x)是连续函数f(x)的一个原函数,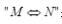
表示“M的充分必要条件是N”,则必有( )。A.F(x)是偶函数f(x)是奇函数
B.F(x)是奇函数f(x)是偶函数
C.F(x)是周期函数f(x)是周期函数
D.F(x)是单调函数f(x)是单调函数答案:A解析:
-
第6题:
设f(x)是连续函数,
(Ⅰ)利用定义证明函数 可导,且F’(x)=f(x);
可导,且F’(x)=f(x);
(Ⅱ)当f(x)是以2为周期的周期函数时,证明函数 也是以2为周期的周期函数.答案:解析:
也是以2为周期的周期函数.答案:解析:



-
第7题:
下列命题中,正确的是( ).A.单调函数的导函数必定为单调函数
B.设f´(x)为单调函数,则f(x)也为单调函数
C.设f(x)在(a,b)内只有一个驻点xo,则此xo必为f(x)的极值点
D.设f(x)在(a,b)内可导且只有一个极值点xo,f´(xo)=0答案:D解析:可导函数的极值点必定是函数的驻点,故选D. -
第8题:
若 f(x)是连续函数,则下列命题不正确的是( )。 答案:A解析:
答案:A解析:
-
第9题:
设f(x)是连续函数,F(x)是f(x)的原函数,则()。
A.当f(x)是奇函数时,F(x)必是偶函数
B.当f(x)是偶函数时,F(x)必是奇函数
C.当f(x)是周期函数时,F(x)必是周期函数
D.当f(x)是单调增函数时,F(x)必是单调增函数答案:B解析: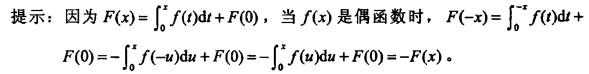
-
第10题:
设f(x)是R上的函数,则下列叙述正确的是()。
- A、f(x)f(-x)是奇函数
- B、f(x)|f(x)|是奇函数
- C、f(x)-f(-x)是偶函数
- D、f(x)+f(-x)是偶函数
正确答案:D -
第11题:
设函数f(x)=丨x丨,则函数在点x=0处()
- A、连续且可导
- B、连续且可微
- C、连续不可导
- D、不可连续不可微
正确答案:C -
第12题:
单选题设F(x)是连续函数f(x)的一个原函数,“M⇔N”表示“M的充分必要条件是N”,则必有( )。AF(x)是偶函数⇔f(x)是奇函数
BF(x)是奇函数⇔f(x)是偶函数
CF(x)是周期函数⇔f(x)是周期函数
DF(x)是单调函数⇔f(x)是单调函数
正确答案: C解析:
采用举例的方法进行排除,令f(x)=x,在(-∞,+∞)内单调增加,但是F(x)=x2/2+C在(-∞,+∞)内不单调,D项错误;
令f(x)=x2为偶函数,但是F(x)=x3/3+C,其中C≠0时不是奇函数,故B项错误;
令f(x)=1+cosx是以2π为周期的函数,但是F(x)=x+sinx+C不是周期函数,故C项错误。 -
第13题:
下列命题正确的是().
A若|f(x)|在x=a处连续,则f(x)在x=a处连续
B若f(x)在x=a处连续,则|f(x)|在x=a处连续
C若f(x)在x=a处连续,则f(x)在z-a的一个邻域内连续
D若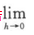 [f(a+h)-f(a-h)]=0,则f(x)在x=a处连续答案:B解析:
[f(a+h)-f(a-h)]=0,则f(x)在x=a处连续答案:B解析:
-
第14题:
下列命题中,错误的是( ).A.设f(x)为奇函数,则f(x)的傅里叶级数是正弦级数
B.设f(x)为偶函数,则f(x)的傅里叶级数是余弦级数
C.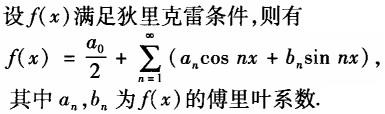
D.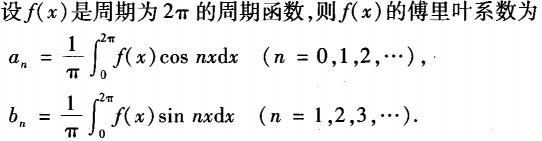 答案:C解析:
答案:C解析:
-
第15题:
设f(x)、f'(x)为已知的连续函数,则微分方程y'+ f'(x)y = f(x)f'(x)的通解是: 答案:C解析:提示:对关于y、y'的一阶线性方程求通解。其中P(x)=f'(x)、Q(x)=f(x) * f'(x),
答案:C解析:提示:对关于y、y'的一阶线性方程求通解。其中P(x)=f'(x)、Q(x)=f(x) * f'(x),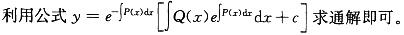
-
第16题:
设函数f(x)在区间[a,b]上连续,则下列结论中哪个不正确?
D.f(x)在[a,b]上是可积的答案:A解析:提示:f(x)在[a,b]上连续,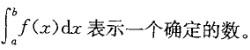
-
第17题:
下列命题正确的是()A.函数f(x)的导数不存在的点,一定不是f(x)的极值点
B.若x0为函数f(x)的驻点,则x0必为f(x)的极值点
C.若函数f(x)在点x0处有极值,且f'(x0)存在,则必有f'(x0)=0
D.若函数f(x)在点x0处连续,则f'(x0)一定存在答案:C解析:根据函数在点x0处取极值的必要条件的定理,可知选项C是正确的. -
第18题:
如果函数f(x,y)在(0,0)处连续,那么下列命题正确的是 答案:B解析:
答案:B解析: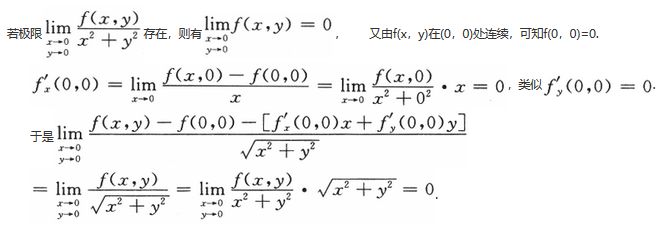
由微分定义知f(x,y)在(0,0)处可微,故应选(B).【评注】1.本题主要考查二元函数连续、偏导数、可微的定义.
2.可采用举反例排除错误答案.取f(x,y)=|x|+|y|排除(A),f(x,y)=x+y排除(C)、(D). -
第19题:
设f(x)为[a,b]上的连续函数,则下列命题不正确的是( )。A.f(x)在[a,b]上有最大值
B.f(x)在[a,b]上一致连续
C.f(x)在[a,b]上可积
D.f(x)在[a,b]上可导答案:D解析:本题主要考查连续函数的特点。f(x)为[a,b]上的连续函数,则f(x)具有有界性,因此A、B、C三项都正确。可导的函数一定连续,但连续的函数不一定可导,所以D项错误。 -
第20题:
设?(x)为开区间(a,b)上的可导函数,则下列命题正确的是( )A.(x)在(a,b)上必有最大值
B.(x)在(a,b)上必一致连续
C.(x)在(a,b)上必有界
D.(x)在(a,b)上必连续答案:D解析:根据微积分的知识,可导的函数必连续,


-
第21题:
设f(x)在(-a,a)(a>0)上连续,F(x)是f(x)的一个原函数,则当f(x)是奇函数时,下面结论正确的是()。
- A、F(x)是偶函数
- B、F(x)是奇函数
- C、F(x)可能是奇函数,也可能是偶函数
- D、F(x)是否为奇函数不能确定
正确答案:A -
第22题:
设f(x)在(-a,a)(a>0)上连续,F(x)是f(x)的一个原函数,则当f(x)是偶函数时,下面结论正确的是()。
- A、F(x)是偶函数
- B、F(x)是奇函数
- C、F(x)可能是奇函数,也可能是偶函数
- D、F(x)是否是偶函数不能确定
正确答案:D -
第23题:
单选题设f(x)是定义在[-a,a]上的任意函数,则下列答案中哪个函数不是偶函数?()Af(x)+f(-x)
Bf(x)·f(-x)
C[f(x)]2
Df(x2)
正确答案: B解析: 暂无解析
