级数前n项和Sn=a1+a2+...+an,若an≥0,判断数列﹛Sn﹜有界是级数收敛的什么条件? A.充分条件,但非必要条件 B.必要条件,但非充分条件 C.充分必要条件 D.既非充分条件,又非必要条件
题目
级数前n项和Sn=a1+a2+...+an,若an≥0,判断数列﹛Sn﹜有界是级数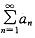 收敛的什么条件?
收敛的什么条件?
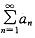 收敛的什么条件?
收敛的什么条件?
A.充分条件,但非必要条件
B.必要条件,但非充分条件
C.充分必要条件
D.既非充分条件,又非必要条件
B.必要条件,但非充分条件
C.充分必要条件
D.既非充分条件,又非必要条件
相似考题
更多“级数前n项和Sn=a1+a2+...+an,若an≥0,判断数列﹛Sn﹜有界是级数收敛的什么条件? ”相关问题
-
第1题:
下列命题中,哪个是正确的?A.周期函数f(x)的傅立叶级数收敛于f(x)
B.若f(x)有任意阶导数,则f(x)的泰勒级数收敛于f(x)
C.若正项级数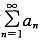 收敛,则
收敛,则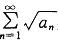 必收敛
必收敛
D.正项级数收敛的充分且必-条件是级数的部分和数列有界答案:D解析:提示:本题先从熟悉的结论着手考虑,逐一分析每一个结论。选项D是正项级数的基本定理,因而正确,其余选项均错误。选项A,只在函数的连续点处级数收敛于f(x);选项B,级数收敛,还需判定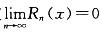 ;选项C,可通过举反例说明,级数
;选项C,可通过举反例说明,级数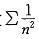 收敛,但
收敛,但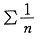 发散。
发散。 -
第2题:
数项级数的部分和数列有界是该级数收敛的( ).A.充分条件
B.必要条件
C.充分必要条件
D.既非充分又非必要条件答案:B解析:按数项级数收敛的定义,级数收敛即级数的部分和数列有极限,而部分和数列有界 是部分和数列有极限的必要条件,故选B. -
第3题:
级数前几项和sn=a1+a2+…+an,若an≥0,判断数列{sn}有界是级数 收敛的什么条件?
收敛的什么条件?
A.充分条件,但非必要条件 B.必要条件,但非充分条件
C.充分必要条件 D.既非充分条件,又非必要条件答案:C解析:提示:用正项级数基本定理判定。 -
第4题:
设{en}是单调增加的有界数列,则下列级数中收敛的是
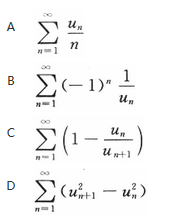 答案:D解析:
答案:D解析:
-
第5题:
设数列an的前n项和为Sn,则数列an是等差数列。(1)Sn=n2+2n,n=1,2,3……(2)Sn=n2+2n+1,n=1,2,3……A.条件(1)充分,但条件(2)不充分
B.条件(2)充分,但条件(1)不充分
C.条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D.条件(1)充分,条件(2)充分
E.条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分答案:A解析:等差数列前n项和Sn的表达式是关于n的二次函数(公差不为0),且无常数项,所以条件(1)充分。 -
第6题:
若级数 收敛,则级数
收敛,则级数 ( )。
( )。
A.必绝对收敛 B.必条件收敛
C.必发散 D.可能收敛,也可能发散答案:D解析:
-
第7题:
(10分)已知数列{an}满足a1=3,an+1= an +2n,
(1)求{ an }的通项公式an;
(2)若bn=n an,求数列{bn}的前n项和sn。答案:解析:
-
第8题:
已知数列{an}的前n项和是Sn,且2Sn+an=1(n∈N*)。
(1)求证:数列{an}是等比数列;
(2)记bn=10+log9an,求{bn}的前n项和Tn的最大值及相应的n值。答案:解析: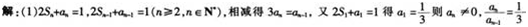
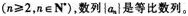
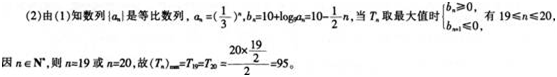
-
第9题:
当n趋于无穷时,级数的一般项的极限为0,则级数()。
- A、肯定收敛
- B、肯定发散
- C、不一定收敛
- D、收敛于0
正确答案:C -
第10题:
下列命题中,错误的是().
- A、部分和数列{s}有界是正项级数收敛的充分条件
- B、若级数绝对收敛,则级数必定收敛
- C、若级数条件收敛,则级数必定发散
- D、若,则级数收敛
正确答案:D -
第11题:
单选题数项级数的部分和数列有界是该级数收敛的().A充分条件
B必要条件
C充分必要条件
D既非充分又非必要条件
正确答案: C解析: 按数项级数收敛的定义,级数收敛即级数的部分和数列有极限,而部分和数列有界是部分和数列有极限的必要条件,故选(B). 注意:对正项级数来说,部分和数列有界是级数收敛的充分必要条件;而对一般的非正项级数来说,部分和数列有界仅是级数收敛的必要条件,而不是充分条件. -
第12题:
单选题已知数列{an}是公差为d的等差数列,Sn是其前n项和,且有S9<S8=S7,则下列说法中不正确的是( )。AS9<S10
Bd<0
CS7与S8均为Sn的最大值
Da8=0
正确答案: B解析:
由S9<S8,可知a9<0,由S8=S7,可知a8=0,所以d<0,所以B、D两项正确;由d<0可知S9以后所有和都小于S8=S7,所以C项正确,A项错误。 -
第13题:
设an>0(n=1,2,…),Sn=a1+a2+…+an,则数列{Sn}有界是数列{an}收敛的A.充分必要条件
B.充分非必要条件
C.必要非充分条件
D.既非充分也非必要条件答案:B解析:
-
第14题:
下列命题中,哪个是正确的?
A.周期函数f(x)的傅立叶级数收敛于f (x)
B.若f(x)有任意阶导数,则f(x)的泰勒级数收敛于f(x)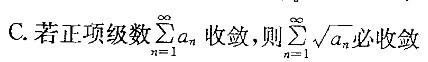
D.正项级数收敛的充分且“条件是级数的部分和数列有界答案:D解析:提示:本题先从熟悉的结论着手考虑,逐一分析每一个结论。选项D是正项级数的基本定理,因而正确,其余选项均错误。选项A,只在函数的连续点处级数收敛于f(x);选项B,级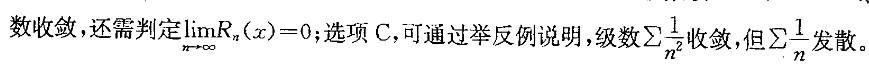
-
第15题:
已知等差数列{an}中,a1=21,Sn是它的前n项之和,S7=S15。
(1)求Sn;
(2)这个数列的前多少项之和最大 求出最大值。答案:解析:(1)设等差数列的公差为d,由题意可得:
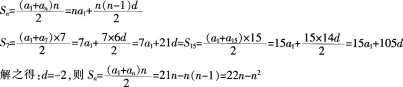
(2)Sn=22n-n2=-(n-11)2+121,当n=11时,数列之和最大,最大值为121。 -
第16题:
已知数列{an}中,Sn是它的前n项和,并且Sn+1=4an+2,a1=1.
(Ⅰ)设bn=an+1-2an,求证:数列{bn)是等比数列;
(Ⅱ)设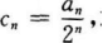 求证:数列{cn}是等差数列;
求证:数列{cn}是等差数列;
(Ⅲ)求数列{an}的通项公式及前n项和.答案:解析:
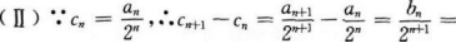


-
第17题:
设0≤an≤1/n(n=1,2,…),下列级数中绝对收敛的是( )。 答案:C解析:提示:因为0n≤1/n(n=1,2,…),所以0≤an2≤1/n2,故
答案:C解析:提示:因为0n≤1/n(n=1,2,…),所以0≤an2≤1/n2,故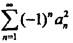 绝对收敛。
绝对收敛。 -
第18题:
若级数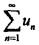 收敛,则下列级数中不收敛的是( )。
收敛,则下列级数中不收敛的是( )。
 答案:D解析:
答案:D解析: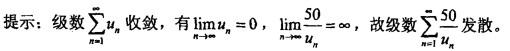
-
第19题:
(10分)已知数列{an}的前n项和Sn=2n+1-k(其中k为常数):
(1)求数列{ an }的通项公式;(4分)
(2)若a1=2,求数列{n an }的前n项和Tn。(6分)答案:解析:
-
第20题:
数列{an}的前n项和为Sn,若an=1/n(n+1),则S5等于()。
- A、1
- B、5/6
- C、1/6
- D、1/30
正确答案:B -
第21题:
数项级数的部分和数列有界是该级数收敛的().
- A、充分条件
- B、必要条件
- C、充分必要条件
- D、既非充分又非必要条件
正确答案:B -
第22题:
单选题当n趋于无穷时,级数的一般项的极限为0,则级数()。A肯定收敛
B肯定发散
C不一定收敛
D收敛于0
正确答案: B解析: 暂无解析 -
第23题:
单选题下列命题中,错误的是().A部分和数列{s}有界是正项级数收敛的充分条件
B若级数绝对收敛,则级数必定收敛
C若级数条件收敛,则级数必定发散
D若,则级数收敛
正确答案: A解析: 暂无解析
