设f(x)是二阶常系数非齐次线性微分方程y″+py′+qy=sin2x+2ex的满足初始条件f(0)=f′(0)=0的特解,则当x→0时, A.不存在 B.等于0 C.等于1 D.其他
题目
B.等于0
C.等于1
D.其他
相似考题
参考答案和解析
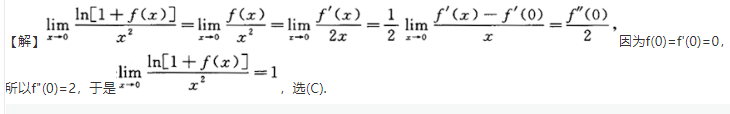
更多“设f(x)是二阶常系数非齐次线性微分方程y″+py′+qy=sin2x+2ex的满足初始条件f(0)=f′(0)=0的特解,则当x→0时, ”相关问题
-
第1题:
微分方程cosydx+(1+e-x)sinydy=0满足初始条件y x=0=π/3的特解是( )。 答案:A解析:提示:方法1求解微分方程,得通解1+ex==Ccosy,再代入初始条件,C= 4, 应选A。方法2代入方程和初始条件检验,可知应选A。
答案:A解析:提示:方法1求解微分方程,得通解1+ex==Ccosy,再代入初始条件,C= 4, 应选A。方法2代入方程和初始条件检验,可知应选A。 -
第2题:
二阶线性常系数齐次微分方程y″+2y=0的通解为____.答案:解析:
-
第3题:
设f1(x)和f2(x)为二阶常系数线性齐次微分方程y″+py′+g=0的两个特解,若由f1(x)和f2(x)能构成该方程的通解,下列哪个方程是其充分条件()?
- A、f1(x)·f′2(x)-f2(x)f′1(x)=0
- B、f1(x)·f′2(x)-f2(x)·f′1(x)≠0
- C、f1(x)f′2(x)+f2(x)·f′1(x)=0
- D、f1(x)f′2(x)+f2(x)f′1(x)≠0
正确答案:B -
第4题:
设y=f(x)是微分方程y"-2y’+4y=0的一个解,又f(x0)>O,f’(x0)=0,则函数f(x)在点x0().
- A、取得极大值
- B、取得极小值
- C、的某个邻域内单调增加
- D、的某个邻域内单调减少
正确答案:A -
第5题:
填空题若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(C1+C2x)ex,则非齐次方程y″+ay′+by=x满足条件y(0)=2,y′(0)=0的解为y=____。正确答案: -xex+x+2解析:
由题意可知,r=1是已知齐次方程对应的特征方程的二重根,则该特征方程为(r-1)2=r2-2r+1=0,齐次方程为y″-2y′+y=0设y*=Ax+B为已知非齐次方程y″-2y′+y=x的特解,代入y″-2y′+y=x得0-2A+Ax+B=x,则A=1,B=2A=2。故已知非齐次方程的通解为y=(C1+C2x)ex+x+2。又y(0)=2,y′(0)=0,代入以上通解得C1=0,C2=-1。故所求方程特解为y=-xex+x+2。 -
第6题:
单选题设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为( )。Af″(x)+f(x)=0
Bf′(x)+f(x)=0
Cf″(x)+f′(x)=0
Df″(x)+f′(x)+f(x)=0
正确答案: A解析:
由f′(x)=f(π/2-x),两边求导得f″(x)=-f′(π/2-x)=-f[π/2-(π/2-x)]=-f(x),即f″(x)+f(x)=0。 -
第7题:
单选题若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(C1+C2x)ex,则非齐次方程y″+ay′+by=x满足条件y(0)=2,y′(0)=0的解为y=( )。Axex+x2+2
B-xex+x2+2
C-xex+x+2
D-xex+x
正确答案: C解析:
由题意可知,r=1是已知齐次方程对应的特征方程的二重根,则该特征方程为(r-1)2=r2-2r+1=0,齐次方程为y″-2y′+y=0设y*=Ax+B为已知非齐次方程y″-2y′+y=x的特解,代入y″-2y′+y=x得0-2A+Ax+B=x,则A=1,B=2A=2。故已知非齐次方程的通解为y=(C1+C2x)ex+x+2。又y(0)=2,y′(0)=0,代入以上通解得C1=0,C2=-1。故所求方程特解为y=-xex+x+2。 -
第8题:
问答题设二阶线性微分方程y″+P(x)y′+Q(x)y=f(x)的三个特解是y1=x,y2=ex,y3=e2x,试求此方程满足条件y(0)=1,y′(0)=3的特解。正确答案:
由题意可知,Y1=ex-x、Y2=e2x-x是原方程对应齐次方程的两个线性无关的解[因(ex-x)/(e2x-x)≠常数],故原方程的通解为y=C1(ex-x)+C2(e2x-x)+x,由y(0)=1,y′(0)=3,得C1=-1,C2=2。故所求原方程的特解为y=-(ex-x)+2(e2x-x)+x=2e2x-ex。解析: 暂无解析 -
第9题:
单选题设y=f(x)是满足微分方程y″+y′-esinx=0的解,且f′(x0)=0,则f(x)在( )。Ax0的某个邻域内单调增加
Bx0的某个邻域内单调减少
Cx0处取得极小值
Dx0处取得极大值
正确答案: B解析:
将f′(x0)=0代入方程得f″(x0)的符号,从而由极值的充分条件得正确选项。
f(x)满足方程f″(x)+f′(x)-esinx=0,所以有 -
第10题:
单选题设f(x)在(-∞,+∞)可导,x0≠0,(x0,f(x0))是y=f(x)的拐点,则( )。Ax0必是f′(x)的驻点
B(-x0,-f(x0))必是y=-f(-x)的拐点
C(-x0,-f(x0))必是y=-f(x)的拐点
D对∀x>x0与x<x0,y=f(x)的凸凹性相反
正确答案: C解析:
已知y=f(x)与y=-f(-x)的图像是关于原点对称的。那么由(x0,f(x0))是y=f(x)的拐点,就能推出(-x0,-f(x0))是y=-f(-x)的拐点。故选B项。 -
第11题:
设y1(x)、y2(x)是二阶常系数线性微分方程y″+py′+qy=0的两个线性无关的解,则它的通解为______.答案:解析:由二阶线性常系数微分方程解的结构可知所给方程的通解为 其中C1,C2为任意常数.
其中C1,C2为任意常数. -
第12题:
设f(x)在(-∞,+∞)二阶可导,f′(x0)=0。问f(x)还要满足以下哪个条件,则f(x0)必是f(x)的最大值()?
- A、x=x0是f(x)的唯一驻点
- B、x=x0是f(x)的极大值点
- C、f″(x)在(-∞,+∞)恒为负值
- D、f″(x0)≠0
正确答案:C -
第13题:
以为特解的二阶线性常系数齐次微分方程是()。
- A、y"-2y'-3y=0
- B、y"+2y'-3y=0
- C、y"-3y'+2y=0
- D、y"-2y'-3y=0
正确答案:B -
第14题:
单选题设函数f(x)满足关系式f″(x)+[f′(x)]2=x,且f′(0)=0,则( )。Af(0)是f(x)的极大值
Bf(0)是f(x)的极小值
C点(0,f(0))是曲线y=f(x)的拐点
Df(0)不是f(x)的极值,点(0,f(0))也不是曲线y=f(x)的拐点
正确答案: B解析:
已知f″(x)+[f′(x)]2=x,方程两边对x求导得f‴(x)+2f″(x)·f′(x)=1,由f′(0)=0,则f″(0)=0,f‴(0)=1,故在点x=0的某邻域内f″(x)单调增加,即f-″(0)与f+″(0)符号相反,故点(0,f(0))是曲线y=f(x)的拐点。 -
第15题:
单选题设f1(x)和f2(x)为二阶常系数线性齐次微分方程y″+py′+q=0的两个特解,若由f1(x)和f2(x)能构成该方程的通解,下列哪个方程是其充分条件?()Af1(x)f′2(x)-f2(x)f′1(x)=0
Bf1(x)f′2(x)-f2(x)f′1(x)≠0
Cf1(x)f′2(x)+f2(x)f′1(x)=0
Df1(x)f′2(x)+f2(x)f′1(x)≠0
正确答案: C解析: 暂无解析 -
第16题:
单选题设f1(x),f2(x)是二阶线性齐次方程y″+p(x)y′+q(x)y=0的两个特解,则c1f1(x)+c2f2(x)(c1,c2是任意常数)是该方程的通解的充要条件为( )。Af1(x)f2′(x)-f2(x)f1′(x)=0
Bf1(x)f2′(x)+f1′(x)f2(x)=0
Cf1(x)f2′(x)-f1′(x)f2(x)≠0
Df1′(x)f2(x)+f2(x)f1(x)≠0
正确答案: A解析:
要使c1f1(x)+c2f2(x)是方程y″+p(x)y′+q(x)y=0的通解,则须满足f1(x),f2(x)线性无关,即ψ(x)=f1(x)/f2(x)≠k(k为常数)。则ψ′(x)=[f1′(x)f2(x)-f1(x)f2′(x)]/f22(x)≠0,即f1′(x)f2(x)-f1(x)f2′(x)≠0。 -
第17题:
单选题以y1=ex,y2=e-3x为特解的二阶线性常系数齐次微分方程是( )。[2012年真题]Ay″-2y′-3y=0
By″+2y′-3y=0
Cy″-3y′+2y=0
Dy″-2y′-3y=0
正确答案: D解析:
因y1=ex,y2=e-3x是特解,故r1=1,r2=-3是特征方程的根,因而特征方程为r2+2r-3=0。故二阶线性常系数齐次微分方程是:y″+2y′-3y=0。 -
第18题:
单选题(2012)以y1=ex,y2=e-3x为特解的二阶线性常系数齐次微分方程是:()Ay″-2y′-3y=0
By″+2y′-3y=0
Cy″-3y′+2y=0
Dy″+2y′+y=0
正确答案: D解析: 暂无解析 -
第19题:
单选题以为特解的二阶线性常系数齐次微分方程是()。Ay"-2y'-3y=0
By"+2y'-3y=0
Cy"-3y'+2y=0
Dy"-2y'-3y=0
正确答案: C解析: 暂无解析 -
第20题:
单选题设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为( )。Af′(x)+f(x)=0
Bf′(x)-f(x)=0
Cf″(x)+f(x)=0
Df″(x)-f(x)=0
正确答案: D解析:
由f′(x)=f(π/2-x),两边求导得f″(x)=-f′(π/2-x)=-f[π/2-(π/2-x)]=-f(x),即f″(x)+f(x)=0。
