设y=f(x)由cos(xy)十Iny-x=1确定,则=().A.2 B.1 C.-1 D.-2

题目

设y=f(x)由cos(xy)十Iny-x=1确定,则

=().

A.2
B.1
C.-1
D.-2

相似考题

1.设f(x＋1)=x＋cos3x,则f(1)=()A、0B、1C、∏/2D、1+cos1

2.设函数y=f(x)由方程y^3+xy^2+x^2y+6=0确定，求f(x)的极值.

3.设函数，(u)可导，z=f(sin y-sin x)+xy，则=__________.

4.设X的分布函数为F(x)=且Y=X^2－1,则E(XY)=_______.

更多“设y=f(x)由cos(xy)十Iny-x=1确定,则=(). ”相关问题

第1题：

设函数y=f(x)由方程确定，则=________.

答案：1、1
解析：
第2题：

设y=cos3x，则y'=（　　）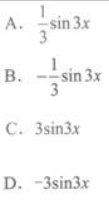

答案：D
解析：
y=cos3x，则y'=sin3x．(3x)'=-3sin3x．因此选D．
第3题：

填空题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。

正确答案： -1/7
解析：
由方程y＝f（x²＋y²）＋f（x＋y）。两边对x求导得y_x′＝f′（x²＋y²）（2x＋2y·y_x′）＋f′（x＋y）（1＋y_x′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|_x_＝₀＝f′（4）·4y′|_x_＝₀＋f′（2）（1＋y′|_x_＝₀），y′|_x_＝₀＝4y′|_x_＝₀＋（1＋y′|_x_＝₀）/2，解得y′|_x_＝₀＝－1/7。
第4题：

单选题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
A
1/5
B
1/7
C
－1/7
D
－1/5

正确答案： B
解析：
由方程y＝f（x²＋y²）＋f（x＋y）。两边对x求导得y_x′＝f′（x²＋y²）（2x＋2y·y_x′）＋f′（x＋y）（1＋y_x′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|_x_＝₀＝f′（4）·4y′|_x_＝₀＋f′（2）（1＋y′|_x_＝₀），y′|_x_＝₀＝4y′|_x_＝₀＋（1＋y′|_x_＝₀）/2，解得y′|_x_＝₀＝－1/7。
第5题：

填空题
设z＝f（xy，x/y）＋g（y/x），其中f、g均可微，则∂z/∂x＝____。

正确答案： yf₁′+f₂′/y-yg′/x²
解析：
设f₁′为函数f（u，v）对第一中间变量的偏导，f₂′为函数f（u，v）对第二中间变量的偏导，g′为函数g对x的导数。则∂z/∂x＝∂f（xy，x/y）/∂x＋∂g（y/x）/∂x＝f₁′y＋f₂′·（1/y）＋g′·（－y/x²）＝f₁′y＋f₂′/y－yg′/x²。
第6题：

单选题
设z＝f（xy，x/y）＋g（y/x），其中f、g均可微，则∂z/∂x＝（　　）。
A
yf₁′＋f₂′/y－yg′/x²
B
yf₁′－f₂′/y－yg′/x²
C
yf₁′－f₂′/y＋yg′/x²
D
yf₁′＋f₂′/y＋yg′/x²

正确答案： A
解析：
设f₁′为函数f（u，v）对第一中间变量的偏导，f₂′为函数f（u，v）对第二中间变量的偏导，g′为函数g对x的导数。则∂z/∂x＝∂f（xy，x/y）/∂x＋∂g（y/x）/∂x＝f₁′y＋f₂′·（1/y）＋g′·（－y/x²）＝f₁′y＋f₂′/y－yg′/x²。
第7题：

单选题
设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝（　　）。
A
（ln2－1）dx
B
（l－ln2）dx
C
（ln2－2）dx
D
ln2dx

正确答案： C
解析：
2^xy＝x＋y等式两边求微分，得2^xyln2d（xy）＝dx＋dy，即2^xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|_x_＝₀＝（ln2－1）dx。
第8题：

填空题
设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝____。

正确答案： 1
解析：
构造函数F（x，y，z）＝x＋y＋z＋xyz，则有∂z/∂x＝－F_x′/F_z′＝－（1＋yz）/（1＋xy），（∂z/∂x）|_（₀_，₁_，－₁_）＝0，又由f（x，y，z）＝e^xyz²，得f_x′＝e^xyz²＋e^xy·2z·z_x′，代入（0，1，－1），得f_x′（0，1，－1）＝e⁰×1×（－1）²＋e⁰×1×2×（－1）×0＝1。
第9题：

单选题
设函数y＝f（x）由方程e2x＋y－cos（xy）＝e－1所确定，则曲线y＝f（x）在点（0，1）处的法线方程为（　　）。
A
y＋1＝x/2
B
y－1＝x/2
C
y＋1＝x
D
y－1＝x

正确答案： B
解析：
e^2x^＋^y－cos（xy）＝e－1方程两边对x求导，得e^2x^＋^y（2＋y′）＋sin（xy）·（y＋xy′）＝0。当x＝0时，y＝1，y′＝－2，因此，法线方程为y－1＝x/2。
第10题：

填空题
设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝____。

正确答案： (ln2-1)dx
解析：
2^xy＝x＋y等式两边求微分，得2^xyln2d（xy）＝dx＋dy，即2^xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|_x_＝₀＝（ln2－1）dx。
第11题：

单选题
函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
A
－x－y＝0
B
x－y－1＝0
C
x－y＝0
D
x＋y＝0

正确答案： A
解析：
xy＋2lnx＝y⁴两端对x求导，得y＋xy′＋2/x＝4y³·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。
第12题：

单选题
设f（x，y）＝ax＋by，其中a，b为常数，则f[xy，f（x，y）]＝（　　）。
A
xy＋bx＋b²y
B
bxy＋ax＋by
C
bxy＋ax－by
D
axy＋abx＋b²y

正确答案： C
解析：
由f（x，y）＝ax＋by知，f[xy，f（x，y）]＝axy＋b（ax＋by）＝axy＋abx＋b²y。
第13题：

设f(x，y)=sin(xy2)，则df(x，y)= .

答案：
解析：
【应试指导】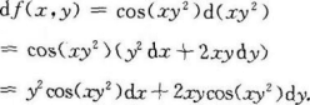
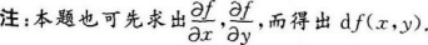
第14题：

设函数y=2x+sinx，则y′=（）

A.1-cos x
B.1+cos x
C.2-cos x
D.2+cos x

答案：D
解析：
第15题：

填空题
设z＝f（x，xy）二阶偏导数连续，则∂2z/∂x∂y＝____。

正确答案： f₂′+xf₁₂″+xyf₂₂″
解析：
∂z/∂x＝f₁′＋yf₂′，∂²z/（∂x∂y）＝f₁₁″·0＋xf₁₂″＋f₂′＋yf₂₂″·x＝xf₁₂″＋f₂′＋xyf₂₂″
第16题：

单选题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
A
1
B
－1
C
1/7
D
－1/7

正确答案： B
解析：
由方程y＝f（x²＋y²）＋f（x＋y）。两边对x求导得y_x′＝f′（x²＋y²）（2x＋2y·y_x′）＋f′（x＋y）（1＋y_x′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|_x_＝0＝f′（4）·4y′|_x_＝0＋f′（2）（1＋y′|_x_＝0），y′|_x_＝0＝4y′|_x_＝0＋（1＋y′|_x_＝0）/2，解得y′|_x_＝0＝－1/7。
第17题：

单选题
设z＝z（x，y）是由方程xz－xy＋ln（xyz）＝0所确定的可微函数，则∂z/∂y等于（　　）。[2013年真题]
A
－xz/（xz＋1）
B
－x＋1/2
C
z（－xz＋y）/[x（xz＋1）]
D
z（xy－1）/[y（xz＋1）]

正确答案： B
解析：
将xz－xy＋ln（xyz）＝0两边对y求偏导，得xz_y′－x＋x（z＋y·z_y′）/（xyz）＝0，整理得z_y′＝z（xy－1）/[y（xz＋1）]。
第18题：

填空题
函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为____。

正确答案： x-y=0
解析：
xy＋2lnx＝y⁴两端对x求导，得y＋xy′＋2/x＝4y³·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。
第19题：

填空题
设f（x，y）＝ax＋by，其中a，b为常数，则f[xy，f（x，y）]＝____。

正确答案： axy+abx+b²y
解析：
由f（x，y）＝ax＋by知，f[xy，f（x，y）]＝axy＋b（ax＋by）＝axy＋abx＋b²y。
第20题：

填空题
已知函数y＝y（x）由方程ey＋6xy＋x2－1＝0所确定，则y″（0）＝____。

正确答案： -2
解析：
e^y＋6xy＋x²－1＝0两边对x求导，得e^y·y′＋6xy′＋6y＋2x＝0①。两边再对x求导，得e^y·y″＋e^y（y′）²＋6xy″＋12y′＋2＝0②。当x＝0时，y＝0，将x＝0，y＝0代入①得y′（0）＝0，再将x＝y＝y′（0）＝0代入②得y″（0）＝－2。
第21题：

填空题
设函数y＝f（x）由方程e2x＋y－cos（xy）＝e－1所确定，则曲线y＝f（x）在点（0，1）处的法线方程为____。

正确答案： y-1=x/2
解析：
e^2x^＋^y－cos（xy）＝e－1方程两边对x求导，得e^2x^＋^y（2＋y′）＋sin（xy）·（y＋xy′）＝0。当x＝0时，y＝1，y′＝－2，因此，法线方程为y－1＝x/2。
第22题：

单选题
设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝（　　）。
A
ln2－1
B
（ln2－1）dx
C
ln2＋1
D
（ln2＋1）dx

正确答案： D
解析：
2^xy＝x＋y等式两边求微分，得2^xyln2d（xy）＝dx＋dy，即2^xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|_x_＝₀＝（ln2－1）dx。
第23题：

单选题
函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
A
x－y＝0
B
x＋y＝0
C
－x－y＝0
D
－x＋y＝0

正确答案： C
解析：
xy＋2lnx＝y⁴两端对x求导，得y＋xy′＋2/x＝4y³·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

设y=f(x)由cos(xy)十Iny-x=1确定,则=().A.2 B.1 C.-1 D.-2

题目

相似考题

更多“设y=f(x)由cos(xy)十Iny-x=1确定,则=(). ”相关问题

相关内容