n阶实对称矩阵A为正定矩阵，则下列不成立的是( )。A.所有k级子式为正(k=1，2，…，n) B.A的所有特征值非负 C. D.秩(A)=n

题目
n阶实对称矩阵A为正定矩阵，则下列不成立的是( )。

A.所有k级子式为正(k=1，2，…，n)
B.A的所有特征值非负
C.
D.秩(A)=n
相似考题

1.若A是____,则A必为方阵。A.对称矩阵B.可逆矩阵C.n阶矩阵的转置矩阵D.线性方程组的系数矩阵

2.n阶对称矩阵A为正定矩阵的充分必要条件是()。A、∣A∣0B、存在n阶矩阵P，使得A=PTPC、负惯性指数为0D、各阶顺序主子式均为正数

3.设A为n阶对称矩阵,则A是正定矩阵的充分必要条件是( ).A.二次型xTAx的负惯性指数零B.存在n阶矩阵C,使得A=CTCC.A没有负特征值D.A与单位矩阵合同

4.n阶对称矩阵A正定的充分必要条件是()。A、|A|0B、存在n阶方阵C使A=CTCC、负惯性指标为零D、各阶顺序主子式均为正数

更多“n阶实对称矩阵A为正定矩阵，则下列不成立的是( )。”相关问题

  • 第1题：

    设A是n阶实对称矩阵，则A有n个()特征值.


    参考答案：实

  • 第2题：

    n阶正交矩阵的乘积是()矩阵。

    A、单位

    B、对称

    C、实

    D、正交


    参考答案：D

  • 第3题：

    N阶实对称矩阵A正定的充分必要条件是().



    A.A无负特征值
    B.A是满秩矩阵
    C.A的每个特征值都是单值
    D.A^-1是正定矩阵

    答案：D
    解析：
    A正定的充分必要条件是A的特征值都是正数，(A)不对；若A为正定矩阵，则A一定是满秩矩阵，但A是满秩矩阵只能保证A的特征值都是非零常数，不能保证都是正数，(B)不对；(C)既不是充分条件又不是必要条件；显然(D)既是充分条件又是必要条件，选(D).

  • 第4题：

    设A,B为n阶对称矩阵,下列结论不正确的是().

    A.AB为对称矩阵
    B.设A,B可逆,则A^-1+B^-1为对称矩阵
    C.A+B为对称矩阵
    D.kA为对称矩阵

    答案：A
    解析：

  • 第5题：

    设N阶矩阵A与对角矩阵合同,则A是().

    A.可逆矩阵
    B.实对称矩阵
    C.正定矩阵
    D.正交矩阵

    答案：B
    解析：

  • 第6题：

    设A是n阶正定矩阵,证明:｜E+A｜>1.


    答案：
    解析：

  • 第7题：

    设A为m阶实对称矩阵且正定，B为m×n实矩阵，B^T为B的转置矩阵，试证：B^TAB为正定矩阵的充分必要条件是B的秩r(B)=n，


    答案：
    解析：

  • 第8题：

    试证：如果A,B都是n阶正定矩阵，则A+B也是正定的


    答案：
    解析：

  • 第9题：

    证明；对任意的n阶矩阵A，为对称矩阵，而为反对称矩阵.


    答案：
    解析：

  • 第10题：

    设A为实对称矩阵,且A的特征值都大于零.证明：A为正定矩阵.


    答案：
    解析：

  • 第11题：

    若矩阵A的所有奇数阶主子式小于零，而所有偶数阶主子式大于零，则该矩阵为（）矩阵。

    • A、正定
    • B、正定二次型
    • C、负定
    • D、负定二次型

    正确答案:C

  • 第12题：

    单选题
    若矩阵A的所有奇数阶主子式小于零，而所有偶数阶主子式大于零，则该矩阵为（）矩阵。
    A

    正定

    B

    正定二次型

    C

    负定

    D

    负定二次型


    正确答案： C
    解析： 暂无解析

  • 第13题：

    设A,B是正定实对称矩阵，则().

    A. AB,A+B一定都是正定实对称矩阵

    B. AB是正定实对称矩阵，A+B不是正定实对称矩阵

    C. A+B是正定实对称矩阵，AB不一定是正定实对称矩阵

    D. AB必不是正定实对称矩阵，A+B必是正定实对称矩阵


    参考答案C

  • 第14题：

    设A,B为,N阶实对称矩阵,则A与B合同的充分必要条件是().

    A.r(A)=r（B）
    B.｜A｜=｜B｜
    C.A～B
    D.A,B与同一个实对称矩阵合同

    答案：D
    解析：
    因为A，B与同一个实对称矩阵合同，则A，B合同.反之，若A，B合同，则A，B的正、负惯性指数相同，从而A，B与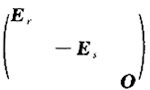合同，选(D).

  • 第15题：

    若A是实对称矩阵，则若|A|＞O，则A为正定的


    答案：错
    解析：

  • 第16题：

    设n阶矩阵A与对角矩阵相似,则().

    A.A的n个特征值都是单值
    B.A是可逆矩阵
    C.A存在n个线性无关的特征向量
    D.A一定为n阶实对称矩阵

    答案：C
    解析：
    矩阵A与对角阵相似的充分必要条件是其有n个线性无关的特征向量，A有n个单特征值只是其可对角化的充分而非必要条件，同样A是实对称阵也是其可对角化的充分而非必要条件，A可逆既非其可对角化的充分条件，也非其可对角化的必要条件，选(C).

  • 第17题：

    若A是实对称矩阵，则A为正定矩阵的充要条件是A的特征值全为正


    答案：对
    解析：

  • 第18题：

    设A为n阶对称矩阵，k为常数.试证kA仍为对称矩阵.


    答案：
    解析：

  • 第19题：

    设Α是正定矩阵，B是实对称矩阵，证明ΑB可对角化


    答案：
    解析：

  • 第20题：

    设A为n阶正定矩阵,证明：对任意的可逆矩阵P,P^TAP为正定矩阵.


    答案：
    解析：

  • 第21题：

    设A,B为n阶正定矩阵.证明：A+B为正定矩阵.


    答案：
    解析：

  • 第22题：

    设A为m阶正定矩阵,B为m×n阶实矩阵.证明：B^SAB正定的充分必要条件是r(B)=n,


    答案：
    解析：

  • 第23题：

    n阶实对称矩阵A为正定矩阵，则下列不成立的是（）。

    • A、所有k级子式为正（k=1，2，…，n）
    • B、A的所有特征值非负
    • C、秩（A）=n

    正确答案:A

相关内容