设F（x）是f（x）的一个原函数，则∫e-x f（e-x ）dx等于下列哪一个函数？ A.F（e-x）+c B.-F（e-x）+c C.F（ex）+c D.-F（ex）+c

题目
设F（x）是f（x）的一个原函数，则∫e-x f（e-x ）dx等于下列哪一个函数？

A.F（e-x）+c
B.-F（e-x）+c
C.F（ex）+c
D.-F（ex）+c
相似考题

1.求微分方程dy/dx +y=e-x的通解．

2.设函数f(x)为奇函数,g(x)为偶函数,则复合函数()是奇函数。A.f(f(x))B.g(f(x))C.f(g(x))D.g(g(x))

3.，是下列中哪个函数？ A.f'(x)的一个原函数 B.f'(x)的全体原函数 C.f(x)的一个原函数 D.f(x)的全体原函数

4.设y=f(－x),则y`=()。A.f`(x)B.-f`(x)C.f`(-x)D.-f`(-x)

参考答案和解析
答案：B
解析：
更多“设F（x）是f（x）的一个原函数，则∫e-x f（e-x ）dx等于下列哪一个函数？ A.F（e-x）+c B.-F（e-x）+c C.F（ex）+c D.-F（ex）+c”相关问题

  • 第1题：

    如果f(x)=e-x，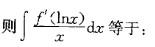
    A. -1/x+c
    B. 1/x+c
    C. -lnx+c
    D. lnx+c


    答案：B
    解析：
    提示:用凑微分法把式子写成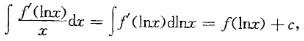再把lnx代入

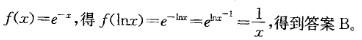
  • 第2题：

    设f(x)函数在[0,+∞)上连续，则f(x)是：
    A. xe-x
    B.xe-x-ex-1
    C. ex-2
    D. (x-1)e-x


    答案：B
    解析：
    提示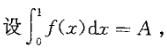：于是原题化为f(x)=xe-x+Aex......①

    分别计算出定积分值：

  • 第3题：

    方程y"-2y'+5y=0的通解为( )。

    A y=ex(c1cosx+c2sinx)
    B y=e-x(c1cos2x+c2sin2x)
    C y=ex(c1cos2x+c2sin2x)
    D y=e-x(c1cosx+c2sinx)

    答案：C
    解析：
    特征方程为λ2-2λ+5=0，其根λ=1±2i，所求通解为 y=ex(c1cos2x+c2sin2x)

  • 第4题：


    A、 y1=x，y2=ex
    B、 y1=e-x，y2=ex
    C、 y1=e-x，y2=xe-x
    D、 y1=ex，y2=xex

    答案：D
    解析：

  • 第5题：

    设f(x)函数在[0,+∞)上连续，且满足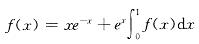，则f(x)是：

    A. xe-x
    B. xe-x-ex-1
    C. ex-2
    D. (x-1)e-x

    答案：B
    解析：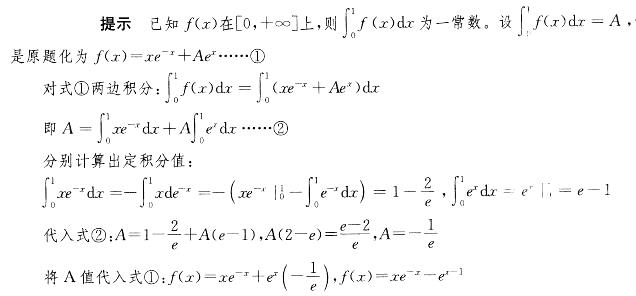

  • 第6题：

    设F(x)是f(x)的一个原函数,则∫e-x f(e-x)dx等于( )。
    A. F(e-x) + C B. -F(e-x)+ C
    C. F(ex) + C D. -F(ex) +C


    答案：B
    解析：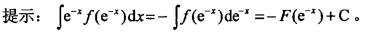

  • 第7题：

    如果f（x）=e-x，则［f′（lnx）／x］dx等于：（）

    • A、-（1／x）+c
    • B、1／x+c
    • C、-lnx+c
    • D、1nx+c

    正确答案:B

  • 第8题：

    设F（x）是f（x）的一个原函数，则等于（）。

    • A、F（e-x）+C
    • B、-F（e-x）+C
    • C、F（ex）+C
    • D、-F（ex）+C

    正确答案:B

  • 第9题：

    单选题
    方程y"+2y’+y=0的通解为（）。
    A

    y=C1ex+C2e-x

    B

    y=e-x（C1+C2x）

    C

    y=C1ex+C2e2x

    D

    y=C1e-x+C2e-2x


    正确答案： C
    解析： 齐次线性方程的特征方程为λ2+2λ+1=0，即（λ+1）2=0，特征根为λ=-1为二重根，故通解为y=e-x（C1+C2x）

  • 第10题：

    单选题
    如果f（x）=e-x，则［f′（lnx）／x］dx等于：（）
    A

    -（1／x）+c

    B

    1／x+c

    C

    -lnx+c

    D

    1nx+c


    正确答案： C
    解析： 暂无解析

  • 第11题：

    单选题
    设f（x）的一个原函数为xex，则∫xf′（x）dx＝（　　）。
    A

    x2ex/2

    B

    x2ex＋C

    C

    2xex＋C

    D

    x2ex/2＋C


    正确答案： B
    解析：
    采用分部积分法，∫xf′（x）dx＝∫xd[f（x）]＝xf（x）－∫f（x）dx，又由题意可知，f（x）＝（xex）′，则∫xf′（x）dx＝x（xex）′－xex＋C＝x2ex＋C。

  • 第12题：

    单选题
    微分方程y″－2y′＋y＝0的两个线性无关的特解是（　　）。[2016年真题]
    A

    y1＝x，y2＝ex

    B

    y1＝e－x，y2＝ex

    C

    y1＝e－x，y2＝xe－x

    D

    y1＝ex，y2＝xex


    正确答案： D
    解析：
    本题中，二阶常系数线性微分方程的特征方程为：r2－2r＋1＝0，解得：r1＝r2＝1，故方程的通解为：y2＝ex（c1＋c2x），则两个线性无关解为c1ex、c2xex（c1、c2为常数）。

  • 第13题：

    设F(x)是f(x)的一个原函数，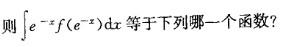
    A.F(e-x)+c B. -F(e-x)+c
    C.F(ex)+c D. -F(ex)+c


    答案：B
    解析：

  • 第14题：

    设F（x）是f（x）的一个原函数，则∫e-x f（e-x ）dx等于下列哪一个函数？

    A.F（e-x）+c
    B.-F（e-x）+c
    C.F（ex）+c
    D.-F（ex）+c

    答案：B
    解析：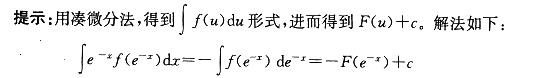

  • 第15题：

    设函数f(x)＝ex，则．f(x－a)·f(x＋a)＝（　　）

    A.f(x2－a2)
    B.2f(x)
    C.f(x2)
    D.f2(x)

    答案：D
    解析：

  • 第16题：

    设F（x）是连续函数f（x）的一个原函数，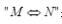

    表示“M的充分必要条件是N”，则必有（　　）。

    A．F（x）是偶函数f（x）是奇函数
    B．F（x）是奇函数f（x）是偶函数
    C．F（x）是周期函数f（x）是周期函数
    D．F（x）是单调函数f（x）是单调函数

    答案：A
    解析：

  • 第17题：

    设f（x）的一个原函数为1nx，则f（x）等于（ ）.《》（ ）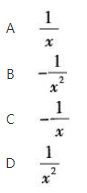


    答案：A
    解析：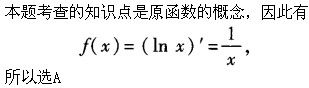

  • 第18题：

    设F（x）是f（x）的一个原函数，则∫e-xf（e-x）dx等于下列哪一个函数？（）

    • A、F（e-x）+c
    • B、-F（e-x）+c
    • C、F（ex）+c
    • D、-F（ex）+c

    正确答案:B

  • 第19题：

    y’+y=e-x的通解为（）。

    • A、y=ex（x+C）
    • B、y=e-x（x+C）
    • C、y=e-x（ex+C）
    • D、y=ex（ex+C）

    正确答案:B

  • 第20题：

    方程y"+2y’+y=0的通解为（）。

    • A、y=C1ex+C2e-x
    • B、y=e-x（C1+C2x）
    • C、y=C1ex+C2e2x
    • D、y=C1e-x+C2e-2x

    正确答案:B

  • 第21题：

    单选题
    微分方程cosydy/dx－siny＝ex的通解为（　　）。
    A

    siny＝（x＋c）ex

    B

    siny＝（x＋c）e－x

    C

    cosy＝（x＋c）ex

    D

    cosy＝（x＋c）e－x


    正确答案： C
    解析：
    原微分方程为cosydy/dx－siny＝ex，令u＝siny，则有du/dx＝cosydy/dx，故原方程可变形为u′－u＝ex。则u＝e∫dx[∫ex·e－∫dxdx＋c]＝（x＋c）ex。故方程的通解为siny＝（x＋c）ex。

  • 第22题：

    单选题
    设F（x）是f（x）的一个原函数，则∫e-xf（e-x）dx等于下列哪一个函数？（）
    A

    F（e-x）+c

    B

    -F（e-x）+c

    C

    F（ex）+c

    D

    -F（ex）+c


    正确答案： C
    解析： 暂无解析

  • 第23题：

    单选题
    设f（x）的一个原函数为xex，则∫xf′（x）dx＝（　　）。
    A

    xex＋C

    B

    x2ex＋C

    C

    －xex＋C

    D

    －x2ex＋C


    正确答案： C
    解析：
    采用分部积分法，∫xf′（x）dx＝∫xd[f（x）]＝xf（x）－∫f（x）dx，又由题意可知，f（x）＝（xex）′，则∫xf′（x）dx＝x（xex）′－xex＋C＝x2ex＋C。

  • 第24题：

    单选题
    设F（x）是f（x）的一个原函数，则等于（）。
    A

    F（e-x）+C

    B

    -F（e-x）+C

    C

    F（ex）+C

    D

    -F（ex）+C


    正确答案： B
    解析： 暂无解析

相关内容