在重置抽样时，假设总体比例为0．2，从此总体中抽取容量为100的样本，则样本比例的标准差为（ ）。A.0．2 B.0．02 C.0．04 D.0．16

题目
在重置抽样时，假设总体比例为0．2，从此总体中抽取容量为100的样本，则样本比例的标准差为（ ）。

A.0．2
B.0．02
C.0．04
D.0．16
相似考题

1.在重置抽样时，假设总体比例为0．2，从此总体中抽取容量为100的样本，则样本比例的标准差为( )。A.0．2B.0．02C.0．04D.0．16

2.从均值为1000、标准差为130的总体中抽取容量为100的样本,则样本均值的标准差为()。A.130B.13C. 1.3D.100

3.样本出例的分布具有以下特征( )。A.样本比例的平均数等于总体平均数，样本比倒的标准差等于总体标准差B.样本比例平均数等于总体平均数，样本标准差等于总体标准差除以样本容量的平方根C. 样本比例的平均数等于总体比例，样本比例的标准差等于总体标准除以样本容量D.样本比例的平均数等于总体比例，样本比例的标准差等于总体比例的标准差除以样本容量的平方根

4.一项研究中要对贫困户的比例进行推断。在95％的置信度下要求误差不超过±3％。采用重置简单随机抽样中，已知z0．025=1．96，则以下说法正确的有( )。A.如果总体中贫困户的比例估计为30％，则必要样本容量为896人B.如果总体中贫困户的比例估计为30％，则必要样本容量为897人C.如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1068人D.如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1067人E.如果缺乏关于总体中贫困户比例的信息，则必要样本容量无法计算

参考答案和解析
答案：C
解析：
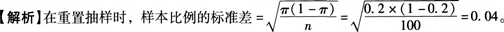
更多“在重置抽样时，假设总体比例为0．2，从此总体中抽取容量为100的样本，则样本比例的标准差为（ ）。”相关问题

  • 第1题：

    按重置抽样方式从总体随机抽取样本量为n的样本。假设总体标准差σ=2，如果样本量n=16增加到n=64，则样本均值的标准差( )。

    A.减少4倍

    B.增加4倍

    C.减少一半

    D.增加一半


    正确答案：C

    当样本量n=16时，样本均值的标准差为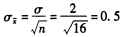；当样本量n=64时，样本均值的标准差为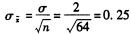：。因此，当样本量从n=16增加到n=64时，样本均值的标准差减少一半。

  • 第2题：

    总体均值为50，标准差为8，从此总体中随机抽取容量为64的样本，则样本均值的抽样分布的均值和标准差分别为（ ）。

    A.50；8
    B.50；1
    C.50；4
    D.8；8

    答案：B
    解析：

  • 第3题：

    从均值为5000，方差为400的正态总体中抽取样本容量为100的一个样本，则重置抽样条件下样本均值的标准误差为（ ）。

    A.400
    B.40
    C.20
    D.2

    答案：D
    解析：

  • 第4题：

    在重置抽样时，假设总体比例为0.2，从此总体中抽取容量为100的样本，则样本比例的标准差为（）。

    • A、0.2
    • B、0.02
    • C、0.04
    • D、0.16

    正确答案:C

  • 第5题：

    抽样的一般程序为（）

    • A、确定样本容量-规定研究总体-抽取样本-判断并纠正抽样偏差
    • B、规定研究总体-确定样本容量-抽取样本-判断并纠正抽样偏差
    • C、规定研究总体-抽取样本-确定样本容量-判断并纠正抽样偏差
    • D、抽取样本-确定样本容量-判断并纠正抽样偏差-规定研究总体

    正确答案:B

  • 第6题：

    从标准差为10的总体抽取容量为50的随机样本，如果采用重复抽样，则样本均值的标准差为（）。

    • A、1.21
    • B、2.21
    • C、1.41
    • D、2.41

    正确答案:C

  • 第7题：

    设总体共有4个元素，从中随机抽取一个容量为2的样本，在重置抽样时，共有16个不同的样本。在不重置抽样时，共有6个可能的样本。


    正确答案:正确

  • 第8题：

    从均值为50，标准差为5的无限总体中抽取容量为30的样本，则抽样分布样本均值超过51的概率为（）。

    • A、0.0987
    • B、0.9013
    • C、0.3256
    • D、0.1357

    正确答案:D

  • 第9题：

    多选题
    一项研究中要对贫困户的比例进行推断。在95%的置信度下要求误差不超过±3%。采用重置简单随机抽样中，已知z0.025=1．96，则以下说法正确的有（）。
    A

    如果总体中贫困户的比例估计为30%，则必要样本容量为896人

    B

    如果总体中贫困户的比例估计为30%，则必要样本容量为897人

    C

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1068人

    D

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1067人

    E

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量无法计算


    正确答案： E,A
    解析： 暂无解析

  • 第10题：

    判断题
    设总体共有4个元素，从中随机抽取一个容量为2的样本，在重置抽样时，共有16个不同的样本。在不重置抽样时，共有6个可能的样本。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第11题：

    单选题
    总体均值为50，标准差为8，从此总体中随机抽取容量为64的样本，则样本均值的抽样分布的均值和标准误分别为（）
    A

    50，8

    B

    50，1

    C

    50，4

    D

    8，8


    正确答案： D
    解析： 暂无解析

  • 第12题：

    单选题
    从标准差为10的总体中抽取一个容量为40的样本，如果采用重复抽样，则样本均值的标准差为（）。
    A

    0.25

    B

    0.5

    C

    0.4

    D

    0.04


    正确答案： B
    解析： 暂无解析

  • 第13题：

    在重置抽样时，样本均值的标准差为总体标准差σ的（ ）。



    答案：B
    解析：

  • 第14题：

    假设总体比例为0.3，采取重置抽样的方法从此总体中抽取一个容量为100的简单随机样本，则样本比例的期望是( )。


    A.0.3

    B.0.8

    C.1.6

    D.2

    答案：A
    解析：
    当样本容量比较大(n =100≥30)时，样本比率p近似服从正态分布，且有p的数学期望就是总体比率π，即：E(p)=π=0.3。

  • 第15题：

    在重置抽样时，样本均值的标准差为总体标准差σ2的1／n。（）


    答案：错
    解析：

  • 第16题：

    假设总体比例为0.3，采取重置抽样的方法从此总体中抽取一个容量为100的简单随机样本，则样本比例的期望是（）。

    • A、0.3
    • B、0.8
    • C、1.6
    • D、2

    正确答案:A

  • 第17题：

    在无放回抽样下，从容量为N的总体中抽取容量为n的样本，则所有可能的样本个数为Nn个。


    正确答案:错误

  • 第18题：

    总体的均值为500，标准差为200，从该总体中抽取一个容量为30的样本，则样本均值的标准差为（）。

    • A、36.51
    • B、30
    • C、200
    • D、91.29

    正确答案:A

  • 第19题：

    按重置抽样方式从总体随机抽取样本量为n的样本。假设总体标准差σ=2，如果样本量n=16增加到n=64，则样本均值的标准误差（）。

    • A、减少4倍
    • B、增加4倍
    • C、减少一半
    • D、增加一半

    正确答案:C

  • 第20题：

    单选题
    假设总体比例为0.3，采取重置抽样的方法从此总体中抽取一个容量为100的简单随机样本，则样本比例的期望是（　　）。
    A

    0.3

    B

    0.8

    C

    1.6

    D

    2


    正确答案： A
    解析： 当样本容量比较大（n=100≥30）时，样本比率p近似服从正态分布，且有p的数学期望就是总体比率π，即：E（p）=π=0.3。

  • 第21题：

    单选题
    样本比例的分布具有的特征是（）。
    A

    样本比例的均值等于总体均值，样本比例的标准差等于总体标准差

    B

    样本比例的均值等于总体均值，样本标准差等于总体标准差除以样本容量的平方根

    C

    样本比例的均值等于总体比例，样本比例的标准差等于总体比例的标准差除以样本容量的平方根

    D

    样本比例的均值等于总体比例，样本比例的标准差等于总体比例的标准差除以样本容量


    正确答案： B
    解析： 暂无解析

  • 第22题：

    单选题
    已知总体的均值为100，标准差为10，从该总体中随机抽取容量为100的样本，则样本均值抽样分布的标准误差为（）
    A

    100

    B

    10

    C

    1

    D

    50


    正确答案： A
    解析： 暂无解析

  • 第23题：

    单选题
    从均值为5000，方差为400的正态总体中抽取样本容量为100的一个样本，则重置抽样条件下样本均值的标准误差为（    ）。
    A

    400

    B

    40

    C

    20

    D

    2


    正确答案： C
    解析：

  • 第24题：

    多选题
    A

    如果总体中贫困户的比例估计为30%，则必要样本容量为896人

    B

    如果总体中贫困户的比例估计为30%，则必要样本容量为897人

    C

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1068人

    D

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1067人

    E

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量无法计算


    正确答案： D,C
    解析：

相关内容