根据某地区2006～2014年农作物种植面积(X)与农作物产值(Y)，可以建立一元线性回归模型，估计结果得到判定系数R2=0．9，回归平方和SSR=90，则估计标准误差为（）。A.1．195 B.1．291 C.3．162 D.3．586

题目
根据某地区2006～2014年农作物种植面积(X)与农作物产值(Y)，可以建立一元线性回归模型，估计结果得到判定系数R2=0．9，回归平方和SSR=90，则估计标准误差为（）。

A.1．195
B.1．291
C.3．162
D.3．586
相似考题

1.根据某地区2006～2014年农作物种植面积(X)与农作物产值(Y)，可以建立一元线性回归模型，估计结果得到判定系数R2=0．9，回归平方和SSR=90，则估计标准误差为( )。A.1．195B.1．291C.3．162D.3．5R6

2.回归平方和占总平方和的比例称为（ ）。A．判定系数(决定系数)B．相关系数C．回归系数D．估计标准误差

3.判定系数r2是用于一元线性回归模型的显著性检验的指标。（ ）

4.已知含有截距项的三元线性回归模型估计的残差平方和为已知含有截距项的三元线性回归模型估计的残差平方和为，估计用样本容量为24，则随机误差项的方差估计量为（）。

参考答案和解析
答案：A
解析：
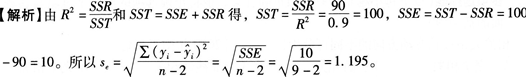
更多“根据某地区2006～2014年农作物种植面积(X)与农作物产值(Y)，可以建立一元线性回归模型，估计结果得到判定系数R2=0．9，回归平方和SSR=90，则估计标准误差为（）。”相关问题

  • 第1题：

    根据某地区2008—2016年农作物种植面积(X)与农作物产值(Y)，可以建立一元线性回归模型，估计结果得到判定系数R2=0．9，回归平方和SSR=90，则估计标准误差为（）。

    A.1.195
    B.1．291
    C.3．162
    D.3．586

    答案：A
    解析：

  • 第2题：

    根据某地区2005-2015年农作物种植面积(X)与农作物产值(Y)，可以建立一元线性回归模型，估计结果得到判定系数R=0.9，回归平方和ESS=90，则回归模型的残差平方和RSS为（ ）。

    A、10
    B、100
    C、90
    D、81

    答案：A
    解析：


    @##

  • 第3题：



    A. x与y的相关系数为0. 963
    B. x与y的相关系数为-0.963
    C. y对x的一元线性回归系数为-1.443
    D. y对x的一元线性回归系数为-0.643
    E. x对y的一元线性回归系数为-0.643


    答案：B,D
    解析：

  • 第4题：

    如果y和x的样本相关系数为0.81，则y对x的线性回归模型的判定系数为（）

    • A、0.19
    • B、0.81
    • C、0.6561
    • D、0.9

    正确答案:C

  • 第5题：

    线性回归模型的判定系数R2可表示为（）

    • A、R2=SSR/SST
    • B、R2=SSE/SST
    • C、R2=1-SSR/SST
    • D、R2=1-SSE/SST
    • E、R2=1-SSR/(SSR+SSE)

    正确答案:B,C,E

  • 第6题：

    一元线性回归方程y^=0.7+0.82x，判定系数等于0.64，则x与y的相关系数为（）

    • A、0.82
    • B、0.64
    • C、0.8
    • D、0.7

    正确答案:C

  • 第7题：

    如果变量X与Y之间无线性相关关系，则（）。

    • A、相关系数为0
    • B、回归系数为0
    • C、判定系数为0
    • D、估计标准误差为0

    正确答案:A,B,C

  • 第8题：

    在一元线性回归分析中，如果估计标准误差为0，则意味着（）。

    • A、回归系数为0
    • B、回归系数为1
    • C、相关系数为0
    • D、相关系数绝对值为1

    正确答案:C,D

  • 第9题：

    单选题
    在确定地区生产总值和国税收入之间是否可以建立一元线性回归模型时，如果两者之间的相关系数r为（），则两者之间高度相关，可以建立一元线性回归模型。
    A

    0.8<

    B

    0.8<

    C

    0.7<

    D

    0.9<


    正确答案： D
    解析： 暂无解析

  • 第10题：

    单选题
    根据某地区2005～2015年农作物种植面积（x）与农作物产值（y），可以建立一元线性回归模型，估计结果得到可决系数R2＝0.9，回归平方和ESS＝90，则回归模型的残差平方和RSS为（　　）。
    A

    10

    B

    100

    C

    90

    D

    81


    正确答案： B
    解析：
    根据公式，R2＝ESS/TSS和TSS＝ESS＋RSS得，TSS＝ESS/R2＝90/0.9＝100，RSS＝TSS－ESS＝100－90＝10。

  • 第11题：

    多选题
    在一元线性回归分析中，如果估计标准误差为0，则意味着（）。
    A

    回归系数为0

    B

    回归系数为1

    C

    相关系数为0

    D

    相关系数绝对值为1


    正确答案： C,D
    解析： 暂无解析

  • 第12题：

    单选题
    根据某地区2010 - 2018年农作物种植面积(x)与农作物产值(Y)，可以建立一元线性回归模型，估计结果得到判定系数R²=0.9，回归平方和SSR =90，则估计标准误差为(    )。
    A

    1.195

    B

    1.291

    C

    3.162

    D

    3.586


    正确答案： A
    解析：

  • 第13题：

    对于一元线性回归模型，以s---e表示估计标准误差，r表示样本相关系数，则有（）。



    答案：D
    解析：

  • 第14题：

    某分析师建立了一元线性回归模型为 C i =β0 +β 1 Y i +u i ，根据已知样本，得到如下估计方程：

    (回答71-72题)
    在显著性水平α =0.05 的条件下，对于该一元回归模型的回归系数显著性分析正确的是（ ）。


    答案：D
    解析：
    判断系数显著性的方法， 应参考 t 显著性水平/2 （样本数量-自由度） ，t 统计值大于 t 显著性水平/2（样本数量-自由度）才能视为通过显著性检验。

  • 第15题：

    在一元线性回归中判定系数等于（）的平方。

    A相关系数

    B回归系数

    C估计标准误

    D总方差


    A
    略

  • 第16题：

    如果一元线性回归方程的估计标准误差说明实际观测值y与估计值完全一致。


    正确答案:正确

  • 第17题：

    回归平方和占总平方和的比例称为（）

    • A、相关系数
    • B、回归系数
    • C、判定系数
    • D、估计标准误差

    正确答案:C

  • 第18题：

    回归平方和占总离差平方和的比例称为（）

    • A、相关系数
    • B、回归系数
    • C、判定系数
    • D、估计标准误差

    正确答案:C

  • 第19题：

    如果变量x与y之间没有线性相关关系，则（）

    • A、相关系数为0
    • B、线性回归系数为0
    • C、可决系数为0
    • D、估计标准误差为0
    • E、变量x与y不一定独立

    正确答案:A,B,C,E

  • 第20题：

    计算题：某公司欲了解广告费用x对销售量y的影响，收集了20个地区的数据，并对x、y进行线性回归分析，得到：方程的截距为364，回归系数为1.42，回归平方和SSR=1602708.6，残差平方和SSE=40158.07。要求： （1）写出广告费用x与销售量y之间的线性回归方程。 （2）假如广告费用投入50000元，根据回归方程估计商品销售量。 （3）计算判定系数R2，并解释它的意义。


    正确答案: （1）销售量y与广告费用x之间的线性回归方程为
    （2）假如广告费用投入50000元，根据回归方程估计商品销售量为71000。
    （3）判定系数R2，，它表示回归平方和SSR占平方和SST的比例为97.6%，回归拟合程度很好。

  • 第21题：

    单选题
    回归平方和占总离差平方和的比例称为（）
    A

    相关系数

    B

    回归系数

    C

    判定系数

    D

    估计标准误差


    正确答案： D
    解析： 判定系数，也叫可决系数或决定系数，在线性回归中，回归平方和与总离差平方和之比值，其数值等于相关系数的平方。

  • 第22题：

    单选题
    回归平方和占总平方和的比例称为（）
    A

    相关系数

    B

    回归系数

    C

    判定系数

    D

    估计标准误差


    正确答案： D
    解析： 暂无解析

  • 第23题：

    单选题
    如果y和x的样本相关系数为0.81，则y对x的线性回归模型的判定系数为（）
    A

    0.19

    B

    0.81

    C

    0.6561

    D

    0.9


    正确答案： A
    解析： 暂无解析

  • 第24题：

    判断题
    如果一元线性回归方程的估计标准误差说明实际观测值y与估计值完全一致。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

相关内容