某医院甲、乙、丙三个科室各有3名医生，且都只有1名男士。现从三个科室中挑选3人支援贫困山区的医疗建设，要求至少有1名男士，且每个科室至少选1人。问有多少种不同的选法?（ ）A．7B．13C．16D．19
题目
某医院甲、乙、丙三个科室各有3名医生，且都只有1名男士。现从三个科室中挑选3人支援贫困山区的医疗建设，要求至少有1名男士，且每个科室至少选1人。问有多少种不同的选法?（ ）
A．7
B．13
C．16
D．19
相似考题
更多“某医院甲、乙、丙三个科室各有3名医生,且都只有1名男士。现从三个科室中挑选3人支援贫困山 ”相关问题
-
第1题：
某医院甲、乙、丙三个科室各有3名医生，且都只有1名男士。现从三个科室中挑选3人支援贫困山区的医疗建设，要求至少有1名男士，且每个科室至少选1人。问有多少种不同的选法？（ ）
A．7
B．13
C．16
D．19
正确答案：D
-
第2题：
寺院里丢失了一袋香火钱，方丈找到甲、乙、丙三个小和尚来询问，三个人逐一陈述，甲说：“我没偷。”乙说：“甲偷了。”丙说：“我没偷。”在一旁的丁了解真相，并发表意见说：“你们三个人中只有一个人偷了，且只有一个人说对了。”
请问，他们三人中到底谁偷了香火钱：?
A乙
B丙
C都没偷
D甲答案：B解析：解析
第一步：翻译题干，找突破口。
（1）甲：-甲；
（2）乙：甲；
（3）丙：-丙；
由题知：丁说的是真话，则根据丁的话，本题为一真题型。甲与乙的话矛盾，矛盾中必有一真一假。因为只有一真，所以丙的话为假。
第二步：分析其余，推出结论。
因为丙的话为假，所以真相是丙偷了，则甲说的是真话，乙说的是假话。
故正确答案为B。 -
第3题：
某医院病房计算机管理中心需要如下信息。 科室：科名、科地址、科电话、医生姓名 病房：病房号、床位号、所属科室名 医生：姓名、职称、所属科室名、年龄、工作证号 病人：病历号、姓名、性别、诊断、主管医生、病房号 其中，一个科室有多个病房、多个医生，一个病房只能属于一个科室，一个医生只属于一个科室，但可负责多个病人的诊治，一个病人的主管医生只有一个。 完成如下设计： （1）设计该计算机管理系统的E-R图。 （2）将该E-R图转换为关系模式。 （3）指出转换结果中每个关系模式的码。
(1)本题的E-R图如图所示。 (2)转换成如下关系模型： 本题的E-R图如图所示。 (2)转换成如下关系模型： -
第4题：
某单位男女员工的人数之比是15∶13。按人数之比5∶7∶8，分为甲、乙、丙三个科室。其中甲科室男女员工的人数之比为4∶3，乙科室为5∶2。则丙科室男女员工人数之比为：A.1∶2
B.2∶3
C.5∶9
D.5∶8答案：C解析：第一步，本题考查基础应用题，用赋值法解题。
第二步，根据男女比为15∶13，则总人数应该为28的倍数；又因为甲∶乙∶丙＝5∶7∶8，则总人数应该为20的倍数；所以赋值总人数为140，则男生人数为75，女生人数为65。甲＝35，乙＝49，丙＝56。又因为甲科室的男女比为4∶3，则甲的男生为20，甲的女生为15，又因为乙科室的男女比为5∶2，则乙的男生为35，乙的女生为14，所以得出丙的男生为75－20－35＝20，丙的女生为65－15－14＝36，则丙的男女比＝20∶36＝5∶9。 -
第5题：
甲、乙两个科室各有4名职员，且都是男女各半。现从两个科室中选出4人参加培训，要求女职员比重不得低于一半，且每个科室至少选1人。问有多少种不同的选法？（ ）
A. 67 B. 63 C. 53 D. 51答案：D解析：由“要求女职负比重不得低于一半”可知，选拔可分为三种情况：（1）2男2女，这种情况下需先从4个女职员中选两个，再从4个男职员中选两个，最后减去4个职员都从一个科室中选出的2 种情形，即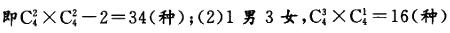
；（3）0男4女，这种情况下只有1种选法。 故共有34 + 16 + 1 = 51（种），D项正确。