甲、乙、丙三个工程队在铺设两条道路,道路A长900米,道路B长1250米。已知甲、乙、丙每天分别能完成道路施工24、30、32米,甲负责道路A,丙负责道路B,乙先帮助甲铺设道路A,然后又去帮助丙铺设道路B。两条道路同时开工同时完工,那么乙队分别帮助甲、丙两队施工多少天?( )A.16天,20天B.10天,15天C.14天,11天D.20天,15天
题目
甲、乙、丙三个工程队在铺设两条道路,道路A长900米,道路B长1250米。已知甲、乙、丙每天分别能完成道路施工24、30、32米,甲负责道路A,丙负责道路B,乙先帮助甲铺设道路A,然后又去帮助丙铺设道路B。两条道路同时开工同时完工,那么乙队分别帮助甲、丙两队施工多少天?( )
A.16天,20天
B.10天,15天
C.14天,11天
D.20天,15天
相似考题
更多“甲、乙、丙三个工程队在铺设两条道路,道路A长900米,道路B长1250米。已知甲、乙、丙每天分别 ”相关问题
-
第1题:
甲、乙、丙三个工程队在铺设两条道路,道路A长900米,道路B长1250米。已知甲、乙、丙每天分别能完成道路施工24、30、32米,甲负责道路A,丙负责道路B,乙先帮助甲铺设道路A,然后又去帮勖丙铺设道路B。两条道路同时开工同时完工,那么乙队分别帮助甲、丙两队施工多少天?( )
A.16天,20天
B.lo天,15天
C.14天,11天
D.20天,15天
正确答案:B
B[解析]道路总长度为900+1250=2150(米),每天三个施工队共可以完成24+30+32=86(米),因此共需要施工2150÷86=25(天)。甲队25天可以完成24×25=600(米),则乙队要帮甲队完成900–600=300(米)再去帮丙队,即乙队帮甲队施工300÷30=10(天)之后,又去帮丙队施工25-10=15(天)。故答案为B。 -
第2题:
某项目有甲、乙、丙三个投资方案,各方案的投资额及内部收益率见下表。若已知基准折现率为10%,则各方案净现值由大到小排序为( )。
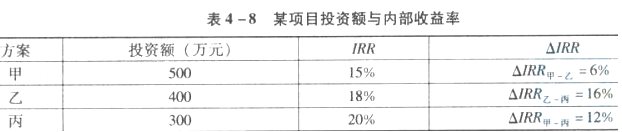 A:甲,乙,丙
A:甲,乙,丙
B:乙,甲,丙
C:乙,丙,甲
D:丙,乙,甲答案:B解析:2019版教材P191
本题考查的是经济效果评价方法。本题可以有两种解法。第一种方法是根据增量内部收益率的判别规则进行排序。解法如下:因为:
△IRR甲-乙=6%<10%,所以乙优于甲,即NPV乙>NPV甲
△IRR乙-丙=16%>10%,所以乙优于丙,即NPVZ>NPV丙
△IRR甲-丙=12%>10%,所以甲优于丙,即NPV甲>NPV丙
所以:NPV乙>NPV甲>NPV丙
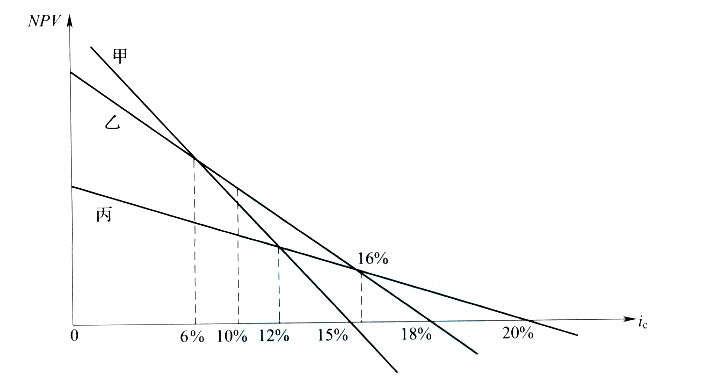
第二种方法是绘图。为了分析简化,将净现值曲线画为直线。由下图可知,当折现率为10%时,净现值由大到小的排序为:乙、甲、丙。
-
第3题:
22、已知甲、乙、丙三个同类型企业职工的平均工资水平相同,但工资的标准差分别是50元、60元和70元,则三个企业职工平均工资的代表性是()。
A.甲好于乙,乙好于丙
B.乙好于甲,甲好于丙
C.丙好于乙,乙好于甲
D.三个企业职工平均工资的代表性无差异
甲好于乙,乙好于丙 -
第4题:
甲、乙、丙三个计算期相同的互斥方案,若有△IRR(乙-甲)>ic,△IRR(丙-乙)<ic,△IRR(丙-甲)>ic,则各方案从优到劣的排列顺序是()。A:甲、乙、丙
B:乙、丙、甲
C:丙、乙、甲
D:乙、甲、丙答案:B解析:根据题目甲、乙、两三个计算期相同的互斥方案,若有△IRR(乙-甲)>ic,则乙方案优于甲方案;根据△IRR(丙-乙)<ic,乙方案优于丙方案;△IRR(丙-甲)>ic,丙方案优于甲方案。所以,甲方案排在最后,其次是丙方案,乙方案最优,乙>丙>甲。 -
第5题:
某工程由甲、乙两工程队合作需要10天完成,乙、丙两个工程队合作需要7天完成,甲、乙、丙三个工程队合作需要5天完成。现甲、乙、丙三个工程队同时工作,2天后,乙工程队因有其他任务撤离该工程,问甲、丙两个工程队还需多少天能完成该工程?( )A.3
B.4
C.5
D.6答案:B解析:设工程总量为70,则甲的效率+乙的效率=70÷10=7,乙的效率+丙的效率=70÷7=10,甲的效率+乙的效率+丙的效率=70÷5=14,则甲的效率=14-10=4,丙的效率=14-7=7。甲、乙、丙前两天共同完成的工作量=14×2=28,剩余工作量=70-28=42。甲、丙同时完成剩余工作量需要天数=42÷(4+7)≈3.8(天),故答案为B。
