两组学生，其中一组参加了古文训练班，另一组没有参加，在语文考试中，参加过古 文训练班的学生比那些没有参加过的学生的平均分数高很多，因此，要想让学生在语文考试中的成绩提高，就必须让他们参加古文训练班。 下列是上述论证依赖的假设是（ ）。 A．很多学生参加了古文训练班 B．学生的父母应该教给学生一些 C．语文成绩的提高与参加古文训练班没有必然的联系 D．只有参加古文训练才能够提高语文成绩

题目

两组学生，其中一组参加了古文训练班，另一组没有参加，在语文考试中，参加过古 文训练班的学生比那些没有参加过的学生的平均分数高很多，因此，要想让学生在语文考试中的成绩提高，就必须让他们参加古文训练班。 下列是上述论证依赖的假设是（ ）。 A．很多学生参加了古文训练班 B．学生的父母应该教给学生一些 C．语文成绩的提高与参加古文训练班没有必然的联系 D．只有参加古文训练才能够提高语文成绩

相似考题

1.下列哪种行为没有侵犯学生的受教育权?()A.不让学习成绩差的学生参加考试。B.在升学、复学方面的不能享受到同等待遇。C.迟送入学通知书，随意开除学生。D.让考试不及格的学生参加补考。

2.某学生语文、数学、英语三科的平均成绩是93分，其中语文、数学平均成绩90分，语文、英语平均成绩93．5分，则该生语文成绩是多少？A．88 B．92 C．95 D．99

3.如果学生选修了某门课后，但没有参加考试，就没有考试成绩记录。查询缺少成绩的学生的学号和相应的课程号。

4.两组学生，其中一组参加了古文训练班，另一组没有参加。在语文考试中，参加过古文训练班的学生比那些没有参加过的学生的平均分数高很多，因此，要想让学生在语文考试中的成绩提高，就必须让他们参加古文训练班。下列是上述论证依赖的假设是：A．很多学生参加了古文训练班B．学生的父母应该教给学生一些古文知识C．语文成绩的提高与参加古文训练班没有必然的联系D．只有参加古文训练才能够提高语文成绩

更多“两组学生，其中一组参加了古文训练班，另一组没有参加，在语文考试中，参加过古 文训练班的学生比那些没有参加过的学生的平均分数高很多，因此，要想让学生在语文考试中的成绩提高，就必须让他们参加古文训练班。 下列是上述论证依赖的假设是（ ）。 A．很多学生参加了古文训练班 B．学生的父母应该教给学生一些 C．语文成绩的提高与参加古文训练班没有必然的联系 D．只有参加古文训练才能够提高语文成绩”相关问题

  • 第1题：

    重修一般针对()的学生。

    A.课程总评成绩未达到60分

    B.考试违纪的学生

    C.因故未参加考试

    D.因故未参加考试，没有申请缓考的学生


    正确答案：A;B;C;D

  • 第2题：

    一些学生参加了“5·12汶川大地震赈灾献爱心”活动，所有班干部都参加了这次活动，只

    有综合成绩为优的学生才能成为班干部。由此可以推知( )。

    A．参加这次活动的学生都是班干部

    B．参加这次活动的学生的综合成绩都为优

    C．综合成绩为良的学生也可以参加这次活动

    D．所有综合成绩为优的学生都参加了这次活动


    正确答案：C
    79．C[解析]这道题考查了考生的演绎推理能力，正确解答该题的关键是理清条件之间的包含关系。题干中“所有班干部都参加了这次活动”说明“一些学生”包括“所有班干部”，但并不一定等于“参加活动的都是班干部”，所以参加这次活动的学生不一定都是班干部，A项不正确。“只有综合成绩为优的学生才能成为班干部”说明“综合成绩为优”是“成为班干部”的前提，但并不一定所有综合成绩为优的学生都是班干部，即综合成绩为优的学生也可以不是班干部，而参加这次活动的学生不一定都是班干部，所以无法推知参加这次活动的非班干部同学的成绩如何，故B、D错误。参加这次活动没有对学生成绩的条件限制，所以“综合成绩为良的学生也可以参加这次活动”，所以本题的正确答案是选项C。

  • 第3题：

    某班有35个学生．每个学生至少参加英语小组、语文小组、数学小组中的一个课外活动小组。现已知参加英语小组的有17人，参加语文小组的有30人，参加数学小组的有13人。如果有5个学生三个小组全参加了，问有多少个学生只参加了一个小组（ ）

    A．15人

    B．16人

    C．17人

    D．18人


    正确答案：A
    设选两门课的人数为A，有(13+17+30)-A-2×5=35，得A=15。所以只报一门的人数为35-15-5=15。

  • 第4题：

    某学生语文、数学、英语三科的平均成绩是93分，其中语文、数学平均成绩90分，语文、英语平均成绩93.5分，则该生语文成绩是多少?

    A．88

    B．92

    C．95

    D．99


    正确答案：A
    [答案]A。[解析] 三科总和为93×3= 279；语文、数学总共180分，那么语文、英语总成绩187，所以英语为279-180=99；数学为 279-187=92；所以语文为88分。

  • 第5题：

    数学老师将上微积分课的一部分学生组成一个学习小组，学习小组的成员获得的平均分要比没有参加学习小组的学生高许多。数学系把小组成员的好成绩归功于参加了学习小组。上述推理的假设是什么?

    A．对老师来讲，微积分是一门很难向一大组学生讲解的课程。

    B．参加学习小组的同学与没有参加学习小组的同学相比，既没有专门准备，也没有受到太多激励。

    C．小组成员花在微积分上的时间并没有影响他们其他课程的成绩。

    D．参加学习小组的同学中很少有人打算学习比微积分更高级的其他数学课。


    正确答案：B
    解析：题干论述：因为参加学习小组，所以成绩好。此类假设往往是：没有其他的原因来解释上面这个事实。既然归功于学习小组，应该跟老师的讲课无关，A项为无关选项。B项表明没有其他的原因，正确。C、D项是无关项。

  • 第6题：

    在某次考试中，学生成绩普遍较差。经核实，学生成绩普遍较差的原因既不是学生学得不好，也不是老师教得不好。所以，我们认为这次考试学生成绩普遍较差的原因是试卷难度过高。
    以下选项如果为真，最能支持以上观点的是：

    A.造成学生在考试中成绩普遍较差的因素很多
    B.学生成绩有波动是正常现象
    C.学校在考试前没有审核试卷难度
    D.学生在考试中成绩普遍较差，或者是因为学生学得不好，或者是因为老师教得不好，或者是因为试卷难度过高

    答案：D
    解析：
    题干通过“学生成绩普遍较差的原因既不是学生学得不好，也不是老师教得不好”得出“这次考试学生成绩普遍较差的原因是试卷难度过高”，选言命题有三个选言肢，否定其中的两个选言肢可以肯定另一个选言肢，所以D项最能支持题干结论；A项削弱了题干结论，B、C两项为无关项。故本题选D。

  • 第7题：

    某校参加数学竞赛的有l20名男生．80名女生，参加语文竞赛的有l20名女生，80名男生。已知该校总共有260名学生参加了竞赛，其中有75．名男生两科都参加了，则只参加数学竞赛而没有参加语文竞赛的女生有( )。


    A. 65人
    B. 60人
    C. 45人
    D. 15人

    答案：D
    解析：
    共有(120+80)×2—260＝140人同时参加两科竞赛，其中女生人数是140—75＝６5人。那么只参加数学竞赛的女生有80—65=l5人。

  • 第8题：

    两组学生，其中一组参加了古文训练班，另一组没有参加，在语文考试中，参加过古文训练班的学生比那些没有参加过的学生的平均分数高很多，因此，要想让学生在语文考试中的成绩提高，就必须让他们参加古文训练班。下列是上述论证以来的假设是：


    A. 很多学生参加了古文训练班
    B. 学生的父母应该教给学生一些
    C. 语文成绩的提高与参加古文训练班没有必然的联系
    D. 只有参加古文训练才能够提高语文成绩

    答案：D
    解析：
    解题指导： 题干的假设必须是只有“参加古文训练”这一途径才“能够提高语文成绩”，若父母的教授也能提高语文成绩，就退不出题干中的结论。故答案为D。

  • 第9题：

    下列哪种行为没有侵犯学生的受教育权？（）

    • A、不让学习成绩差的学生参加考试。
    • B、在升学、复学方面的不能享受到同等待遇。
    • C、迟送入学通知书，随意开除学生。
    • D、让考试不及格的学生参加补考。

    正确答案:D

  • 第10题：

    下列变量中属于比率变量的是（）

    • A、学生的语文考试成绩
    • B、学生在数学竞赛上的名次
    • C、某山海拔2749.08米
    • D、学生在60米跑项目上所用的时间

    正确答案:D

  • 第11题：

    单选题
    下列哪种行为没有侵犯学生的受教育权？（）
    A

    不让学习成绩差的学生参加考试。

    B

    在升学、复学方面的不能享受到同等待遇。

    C

    迟送入学通知书，随意开除学生。

    D

    让考试不及格的学生参加补考。


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    下列变量中属于比率变量的是（）
    A

    学生的语文考试成绩

    B

    学生在数学竞赛上的名次

    C

    某山海拔2749.08米

    D

    学生在60米跑项目上所用的时间


    正确答案： C
    解析： 暂无解析

  • 第13题：

    某校参加数学竞赛的有 120 名男生，80 名女生，参加语文的有 120 名女生，80 名男

    生。已知该校总共有 260名学生参加了竞赛，其中有 75 名男生两科都参加了，问只参加数学

    竞赛而没有参加语文的女生有多少人？( )

    A.65 人

    B.60 人

    C.45 人

    D.15 人


    正确答案：D

  • 第14题：

    某校参加数学竞赛有120名男生、80名女生，参加语文竞赛有120名女生、80名男生。已知该校总共有260名学生参加了竞赛，其中有75名男生两科竞赛都参加了，那么只参加数学竞赛而没有参加语文竞赛的女生有多少人?

    A．15

    B．25

    C．65

    D．75


    正确答案：A
    [答案] A。[解析]此题为比较复杂的容斥问题，有75名男生两科竞赛都参加了，因此至少参加了一项竞赛的男生有120+80-75=125人，那么至少参加一项竞赛的女生有260-125=135人，那么只参加数学竞赛没有参加语文竞赛的女生有135-120=15人。

  • 第15题：

    学生成绩表包括：学号、姓名、数学、语文、计算机、总成绩6个字段，其中数学、语文、计算机和总成绩字段均为N型。要将每个学生的数学、语文、计算机3科成绩汇总后存入“总成绩”字段中，应该使用的命令是______。

    A．REPLACE总成绩WITH数学+语文+计算机

    B．SUM数学+语文+计算机TO总成绩

    C．TOTALON总成绩FIELDS数学，语文，计算机

    D．REPLACEALL总成绩WITH数学+语文+计算机


    正确答案：D

  • 第16题：

    一项调查显示，某班参加挑战杯比赛的同学，与那些未参加此项比赛的同学相比，学习成绩一直保持较高的水平。此项调查得出结论：挑战杯比赛通过开拓学生的视野，增加学生的学习兴趣，激发学生的创造潜力，有效地提高了学生的学习成绩。 以下哪项如果为真，最能加强上述调查结论的说服力?（ ） A．没有参加挑战杯比赛的同学如果通过其他活动开拓视野，也能获得好成绩 B．整天在教室内读书而不参加课外科技活动的学生，他们的视野、学习兴趣和创造力可能会受到影响 C．没有参加挑战杯比赛的同学大都学习很努力 D．参加挑战杯比赛并不以学习成绩好为条件


    正确答案：D
    加强支持型题目。题干以“调查显示”为据，得出结论：参加挑战杯比赛有助于提高学生成绩。A项在“开拓视野”和“获得好成绩”间建立联系，但对于“挑战杯比赛”这一核心概念却未予以加强，反有削弱之意；B项从反面对题干论证进行了加强，但“可能”一词，力度较弱；C项为无关项；D项有力支持了题干的论证，指出题干并未犯“因果倒置”的错误，最有力地加强了调查的说服力。故选D。

  • 第17题：

    某学生语文、数学、英语三科的平均成绩是93分，其中语文、数学平均成绩90分，语文、英语平均成绩93.5分，则该生语文成绩是多少?

    A. 88
    B. 92
    C. 95
    D. 99

    答案：A
    解析：
    三科总和为93×3= 279；语文、数学总共180分，那么语文、英语总成绩187，所以英语为279-180=99；数学为 279-187=92；所以语文为88分。故答案为A。

  • 第18题：

    某教育机构对一所高中全体学生的学习习惯和语文成绩进行了调查研究,结果发现：相比于喜欢大量做习题的学生,喜欢大量阅读课外读物的学生语文成绩更好。因此该机构认为,阅读比做习题更能提高学生的语文成绩。
    以下哪项如果为真,最能支持该机构的观点？（ ）

    A.语文考试对学生的阅读量要求很高
    B.学生之所以做大量习题是因为其语文成绩较差
    C.各项成绩都很优秀的学生才有时间和精力阅读课外读物
    D.其他机构在小学和初中做了同类研究,得出了相反的结论

    答案：A
    解析：

    第一步，确定题型。
    根据提问方式中的“支持”，确定为加强论证。
    第二步，找论点和论据。
    论点：阅读比做习题更能提高学生的语文成绩。
    论据：相比于喜欢大量做习题的学生，喜欢大量阅读课外读物的学生语文成绩更好。
    第三步，辨析选项。
    A项：增加论据。该项提到语文考试对阅读量要求高，具体解释了为什么大量阅读课外读物的学生语文成绩更好，具有加强作用。
    B项：无关选项。该项提到学生做习题的原因是语文成绩差，与论点阅读是否更能提高语文成绩无关，不具有加强作用。
    C项：增加反向论据。该项指出成绩好的学生才有时间阅读，否定了论点阅读更能提高成绩的说法，具有削弱作用。
    D项：无关选项。该项讨论的是其他机构同类研究的结论，与论点中提到的机构无关，不具有加强作用。

  • 第19题：

    有一个64名学生的班级，语文历年考试成绩的u=5，又知今年期中考试语文平均成绩是80分，如果按99%的概率推测，那么该班语文学习的真实成绩可能为()

    A.78
    B.79
    C.80
    D.81

    答案：B,C,D
    解析：
    推断统计；参数估计；总体平均数的估计。

  • 第20题：



    下列说法与资料相符的是：

    A.语文成绩最好的学生，英语成绩也是最好的
    B.数学成绩130分以上的所有学生都没有科目不合格
    C.班上体育成绩得满分的学生占学生总数的25%以上
    D.所有化学成绩超过90分的学生，物理成绩也都超过90分

    答案：C
    解析：
    第一步，本题考查综合分析问题，且需选出正确的一项。
    第二步，A选项，读数比较，定位表格可知，语文成绩最好的是刘红（122），英语成绩最好的是李艳（142），并非同一人，错误。
    B选项，读数比较，定位表格可知，数学成绩130分以上的学生有三人，分别为李艳（133）、章强（130）、陈聪（131），其中陈聪政治科目56分，不及格，错误。
    C选项，求比重，定位表格可知，体育成绩得满分的学生有11人，全班总人数41人。根据比重＝部分量/整体量，代入数据可得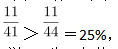，正确。
    D选项，读数比较，定位表格可知，李清华同学化学91分，但物理只有85分，并没有超过90分，错误。
    因此，选择C选项。

  • 第21题：

    现行大学生城镇居民医保大病补充保险个人是如何参保的（）

    • A、已参加大学生城镇居民医保的学生，个人付款参保
    • B、已参加大学生城镇居民医保的学生，学院付款参保
    • C、已参加大学生城镇居民医保的学生，学校付款参保
    • D、已参加大学生城镇居民医保的学生，国家付款参保

    正确答案:D

  • 第22题：

    逻辑老师将上逻辑课的一部分学生组成一个学习小组，学习小组的成员获得的平均分要比没有参加学习小组的学生高许多，所以参加学习小组能够提高学习成绩。上述推理基于以下哪项假设？（）

    • A、学生学逻辑比较困难.
    • B、参加学习小组的学生与没有参加学习小组的学生起点相同
    • C、参加学习小组没有影响其他课程的成绩
    • D、参加学习小组的学生中很少有人打算学习比逻辑更简单的其他课程

    正确答案:B

  • 第23题：

    单选题
    逻辑老师将上逻辑课的一部分学生组成一个学习小组，学习小组的成员获得的平均分要比没有参加学习小组的学生高许多，所以参加学习小组能够提高学习成绩。上述推理基于以下哪项假设？（）
    A

    学生学逻辑比较困难

    B

    参加学习小组的学生与没有参加学习小组的学生起点相同

    C

    参加学习小组没有影响其他课程的成绩

    D

    参加学习小组的学生中很少有人打算学习比逻辑更简单的其他课程


    正确答案： B
    解析： 题干从"参加学习小组的成员获得的平均分比没参加学习小组的学生更高"得出结论：参加学习小组能够提高学习成绩。显然要求"参加学习小组的学生与没有参加学习小组的学生起点相同"作为假设。否则，如果参加学习小组的学生成绩本来就较高，则无法说明参加学习小组能够提高学习成绩，因此B项作为假设是必需的。A、C两项都是无关项；如果D项作为假设，则说明参加学习小组的学生原来起点可能更高，削弱了结论。故选B。

相关内容