若某二叉树的后序遍历序列为KBFDCAE，中序遍历序列为BKEFACD，则该二叉树为 （58）。A.AB.BC.CD.D

题目

若某二叉树的后序遍历序列为KBFDCAE，中序遍历序列为BKEFACD，则该二叉树为 （58）。

A.A

B.B

C.C

D.D

相似考题

1.● 已知一个二叉树的先序遍历序列为①、②、③、④、⑤，中序遍历序列为②、①、④、③、⑤，则该二叉树的后序遍历序列为 （57） 。对于任意一棵二叉树，叙述错误的是 （58） 。（57）A. ②、③、①、⑤、④B. ①、②、③、④、⑤C. ②、④、⑤、③、①D. ④、⑤、③、②、①（58）A. 由其后序遍历序列和中序遍历序列可以构造该二叉树的先序遍历序列B. 由其先序遍历序列和后序遍历序列可以构造该二叉树的中序遍历序列C. 由其层序遍历序列和中序遍历序列可以构造该二叉树的先序遍历序列D. 由其层序遍历序列和中序遍历序列不能构造该二叉树的后序遍历序列

2.若二叉树的先序遍历序列为ABDECF，中序遍历序列DBEAFC，则其后序遍历序列为______。A．DEBAFCB．DEFBCAC．DEBCFAD．DEBFCA

3.若二叉树的先序遍历序列为ABDECF，中序遍历序列为DBEAFC，则其后序遍历序列为(11)。A．DEBAFCB．DEFBCAC．DEBCFAD．DEBFCA

4.若二叉树的先序遍历序列为ABDECF，中序遍历序列为DBEAFC，则其后序遍历序列为(8)。A．DEBAFCB．DEFBCAC．DEBCFAD．DEBFCA

参考答案和解析
正确答案：A
本题考查二叉树的遍历。二叉树的主要遍历方式有：前序遍历、中序遍历、后序遍历、层次遍历。如果已知中序遍历，并知道前序遍历与后序遍历中的任意一个，便可得到一棵唯一的二叉树。具体是怎么做的呢？利用的是遍历的特点。中序遍历的顺序是：左、根、右。而后序遍历的顺序是：左、右、根。回到题目里面来，从“后序遍历序列为KBFDCAE”，可以得知，二叉树的根结点为：E（此时已经可以排除选项C与选项D了）。继续分析，由“中序遍历序列为BKEFACD”，可以得知，二叉树的左子树包括结点：BK。右子树包括结点：FACD。重复上面的步骤，对左子树与左子树看成独立的两棵树进行分析。在后序遍历中，左子树的结点BK的顺序为“KB”，所以B是根结点；右子树的结点FACD的顺序为“FDCA”，所以右子树的根结点为A。当分析到这一步时，已经可以得到本题答案为A。
更多“若某二叉树的后序遍历序列为KBFDCAE,中序遍历序列为BKEFACD,则该二叉树为 (58)。A.AB.B# ”相关问题

  • 第1题：

    ●已知某二叉树的先序遍历序列为ABCD，中序遍历序列为BADC，则该二叉树的后序遍历序列为(39)。

    (39)A.BDCA

    B.CDBA

    C.DBCA

    D.BCDA


    正确答案：A

  • 第2题：

    设某棵二叉树的中序遍历序列为ABCD，先序遍历序列为CABD，则后序遍历该二叉树得到序列为 。

    A．BADC

    B．BCDA

    C．CDAB

    D．CBDA


    BADC

  • 第3题：

    23、设某棵二叉树的中序遍历序列为ABCD，先序遍历序列为CABD，则后序遍历该二叉树得到序列为 。

    A．BADC

    B．BCDA

    C．CDAB

    D．CBDA


    (1) (2)设二叉树的前序遍历序列为P1P2…Pm中序遍历序列为S1S2…Sm。因为前序遍历是“根一左一右”中序遍历是“左一根一右”则前序遍历序列中第一个结点P1是根结点。到中序序列中查询到Si=P1根据中序遍历时根结点将中序序列分成左右两部分的原则有：若i=1即S1=P1则这时的二叉树没有左子树；否则S1S2…Si一1是左子树的中序遍历序列用该序列和前序序列p2P3…Pi去构造该二叉树的左子树。若i=m即Sm=P1则这时的二叉树没有右子树；否则Si (1)(2)设二叉树的前序遍历序列为P1,P2,…,Pm,中序遍历序列为S1,S2,…,Sm。因为前序遍历是“根一左一右”,中序遍历是“左一根一右”,则前序遍历序列中第一个结点P1是根结点。到中序序列中查询到Si=P1,根据中序遍历时根结点将中序序列分成左右两部分的原则,有：若i=1,即S1=P1,则这时的二叉树没有左子树；否则,S1,S2,…,Si一1是左子树的中序遍历序列,用该序列和前序序列p2,P3,…,Pi去构造该二叉树的左子树。若i=m,即Sm=P1,则这时的二叉树没有右子树；否则,Si

  • 第4题：

    已知某二叉树的先序遍历序列为ABCD，后序遍历序列为CDBA，则该二叉树为( )。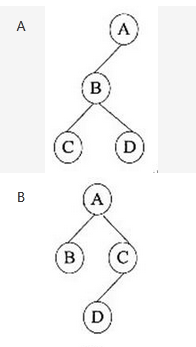



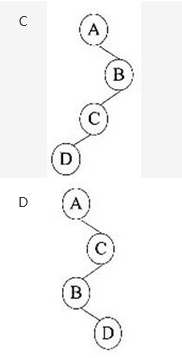    答案：A
    解析：
    本题考查数据结构基础知识。
    对非空的二叉树进行先序遍历的过程是：先访问根结点，然后先序遍历左子树，最后先序遍历右子树。题中四个二叉树的先序遍历序列分别为ABCD、ABCD、ABCD、ACBD。
    对非空的二叉树进行后序遍历的过程是：先后序遍历左子树，接着后序遍历右子树，最后再访问根结点。题中四个二叉树的后序遍历序列分别为CDBA、BDCA、DCBA、DBCA。

  • 第5题：

    如果某二叉树的先序遍历序列为abced，中序遍历序列为cebda，则该二叉树的后序遍历序列是________。

    A．cedba

    B．decba

    C．ecdba

    D．ecbad


    不发生改变

相关内容