阅读以下说明和图，填补流程图中的空缺。【说明】某汽车制造工厂有两条装配线。汽车装配过程如图10-6所示，即汽车底盘进入装配线，零件在多个工位装配，结束时汽车自动完成下线工作。(1)e0和e1表示底盘分别进入装配线0和装配线1所需要的时间。(2)每条装配线有n个工位，第一条装配线的工位为S0,0，S0,1，…，S0,n-0，第二条装配线的工位为S1,0，S1,1，…，S1,n-1。其中S0,k和S1,k(0≤k≤n-1)完成相同的任务，但所需时间可能不同。(3)aij表示在工位Sij处的装配时间，其中i表示
题目
阅读以下说明和图，填补流程图中的空缺。
【说明】
某汽车制造工厂有两条装配线。汽车装配过程如图10-6所示，即汽车底盘进入装配线，零件在多个工位装配，结束时汽车自动完成下线工作。
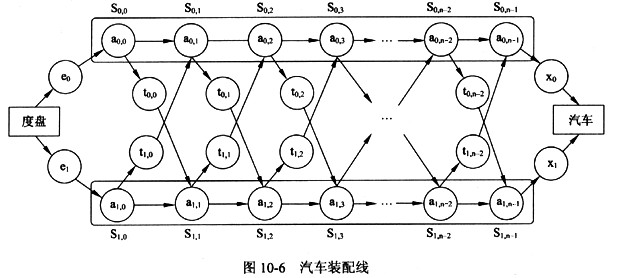
(1)e0和e1表示底盘分别进入装配线0和装配线1所需要的时间。
(2)每条装配线有n个工位，第一条装配线的工位为S0,0，S0,1，…，S0,n-0，第二条装配线的工位为S1,0，S1,1，…，S1,n-1。其中S0,k和S1,k(0≤k≤n-1)完成相同的任务，但所需时间可能不同。
(3)aij表示在工位Sij处的装配时间，其中i表示装配线(i=0或i=1)，j表示工位号(0≤j≤n-1)。
(4)tij表示从Sij处装配完成后转移到另一条装配线下一个工位的时间。
(5)X0和X1表示装配结束后，汽车分别从装配线0和装配线1下线所需要的时间。
(6)在同一条装配线上，底盘从一个工位转移到其下一个工位的时间可以忽略不计。
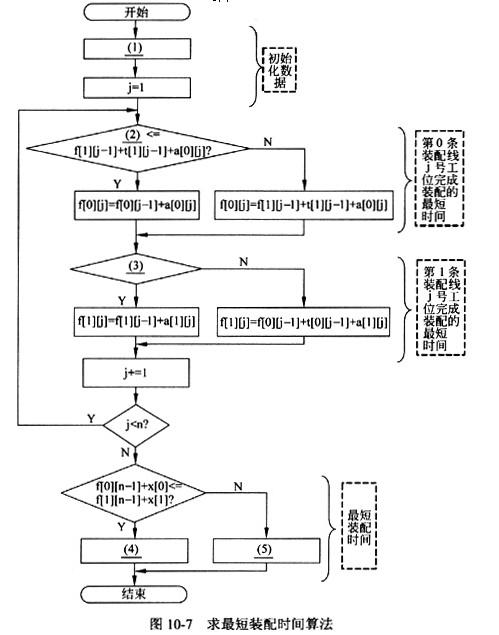
图10-7所示的流程图描述了求最短装配时间的算法，该算法的输入为；
n： 表示装配线上的工位数；
e[i]： 表示e1和e2，i取值为0或1：
a[i][j]： 表示ai,j，i的取值为0或1，j的取值范围为0～n-1；
t[i][j]： 表示ti,j，i的取值为0或1，j的取值范围为0～n-1；
x[i]： 表示X0和X1，i取值为0或1。
算法的输出为：
fi：最短的装配时间；
li：获得最短装配时间的下线装配线号(0或者1)。
算法中使用的f[i][j]表示从开始点到Si,j处的最短装配时间。
相似考题
更多“ 阅读以下说明和图，填补流程图中的空缺。【说明】某汽车制造工厂有两条装配线。汽车装配过程如图10-6所示，即汽车底盘进入装配线，零件在多个工位装配，结束时汽车自动完成下线工作。(1)e0和e1表示底盘分别进入装配线”相关问题
-
第1题：
某汽车加工工厂有两条装配线L1和L2;每条装配线的工位数均为n(Sij，i=1或2，j=1，2,..n)，两条装配线对应的工位完成同样的加工工作，但是所需要的时间可能不同
(aij，i=1或2，j=1，2，... n)。汽车底盘开始到进入两条装配线的时间(e1，e2)以及装配后到结束的时间(X1X2)也可能不相同。从一个工位加工后流到下一个工位需要迁移时间
(tij,i=1或2，j=2,n)。现在要以最快的时间完成一辆汽车的装配，求最优的装配路线。
分析该问题，发现问题具有最优子结构。以L1为例，除了第一个工位之外，经过第j
个工位的最短时间包含了经过L1的第j-1个工位的最短时间或者经过L2的第j-1个工位的最
短时间,如式(1)。装配后到结束的最短时间包含离开L1的最短时间或者离开L2的最短时间
如式(2)。
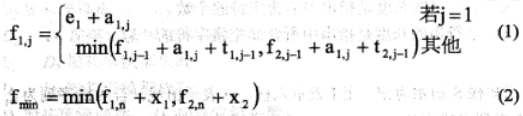
由于在求解经过L1和L2的第j个工位的最短时间均包含了经过L1的第j-1个工位的最
短时间或者经过L2的第j-1个工位的最短时间，该问题具有重复子问题的性质，故采用迭代
方法求解。该问题采用的算法设计策略是(62) ，算法的时间复杂度为(63) 。
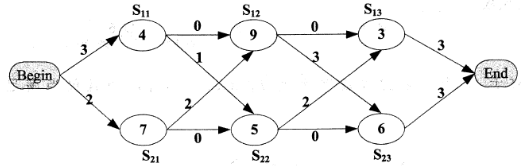
以下是一个装配调度实例，其最短的装配时间为(64) ，装配路线为(65) 。
A.分治
B.动态规划
C.贪心
D.回溯答案：B解析：动态规划算法与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。本题中的时间复杂度为O(n) 。
贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。
回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。
求最短的装配时间与装配路线只需要将选项按照公式带入计算（将图上每条路径上的所有数字相加）可得最短路线为S11→S22→S13 ，时间为21。 -
第2题：
某汽车加工工厂有两条装配线L1和L2;每条装配线的工位数均为n(Sij，i=1或2，j=1，2,..n)，两条装配线对应的工位完成同样的加工工作，但是所需要的时间可能不同
(aij，i=1或2，j=1，2，... n)。汽车底盘开始到进入两条装配线的时间(e1，e2)以及装配后到结束的时间(X1X2)也可能不相同。从一个工位加工后流到下一个工位需要迁移时间
(tij,i=1或2，j=2,n)。现在要以最快的时间完成一辆汽车的装配，求最优的装配路线。
分析该问题，发现问题具有最优子结构。以L1为例，除了第一个工位之外，经过第j
个工位的最短时间包含了经过L1的第j-1个工位的最短时间或者经过L2的第j-1个工位的最
短时间,如式(1)。装配后到结束的最短时间包含离开L1的最短时间或者离开L2的最短时间
如式(2)。
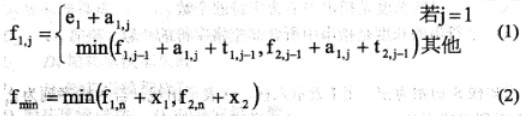
由于在求解经过L1和L2的第j个工位的最短时间均包含了经过L1的第j-1个工位的最
短时间或者经过L2的第j-1个工位的最短时间，该问题具有重复子问题的性质，故采用迭代
方法求解。该问题采用的算法设计策略是(62) ，算法的时间复杂度为(63) 。
以下是一个装配调度实例，其最短的装配时间为(64) ，装配路线为(65) 。
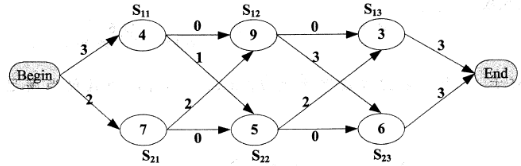A.S11→S12→S13
B.S11→S22→S13
C.S21→S12→S23
D.S21→S22→S23答案：B解析：动态规划算法与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。本题中的时间复杂度为O(n) 。
贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。
回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。
求最短的装配时间与装配路线只需要将选项按照公式带入计算（将图上每条路径上的所有数字相加）可得最短路线为S11→S22→S13 ，时间为21。
-
第3题：
汽车总装配线一般采用工艺原则布置。
错误 -
第4题：
某汽车加工工厂有两条装配线L1和L2;每条装配线的工位数均为n(Sij，i=1或2，j=1，2,..n)，两条装配线对应的工位完成同样的加工工作，但是所需要的时间可能不同
(aij，i=1或2，j=1，2，... n)。汽车底盘开始到进入两条装配线的时间(e1，e2)以及装配后到结束的时间(X1X2)也可能不相同。从一个工位加工后流到下一个工位需要迁移时间
(tij,i=1或2，j=2,n)。现在要以最快的时间完成一辆汽车的装配，求最优的装配路线。
分析该问题，发现问题具有最优子结构。以L1为例，除了第一个工位之外，经过第j
个工位的最短时间包含了经过L1的第j-1个工位的最短时间或者经过L2的第j-1个工位的最
短时间,如式(1)。装配后到结束的最短时间包含离开L1的最短时间或者离开L2的最短时间
如式(2)。
由于在求解经过L1和L2的第j个工位的最短时间均包含了经过L1的第j-1个工位的最
短时间或者经过L2的第j-1个工位的最短时间，该问题具有重复子问题的性质，故采用迭代
方法求解。该问题采用的算法设计策略是(62) ，算法的时间复杂度为(63) 。
以下是一个装配调度实例，其最短的装配时间为(64) ，装配路线为(65) 。
A.O（lgn）
B.O（n）
C.O（n2）
D.O（nlgn）答案：B解析：动态规划算法与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。本题中的时间复杂度为O(n) 。
贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。
回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。
求最短的装配时间与装配路线只需要将选项按照公式带入计算（将图上每条路径上的所有数字相加）可得最短路线为S11→S22→S13 ，时间为21。 -
第5题：
汽车变速箱装配线生产节拍最高可达1小时。
D