阅读下列说明和c函数代码，将应填入 (n) 处的字句写在答题纸的对应栏内。【说明】对二叉树进行遍历是二叉树的一个基本运算。遍历是指按某种策略访问二叉树的每个结点，且每个结点仅访问一次的过程。函数InOrder。()借助栈实现二叉树的非递归中序遍历运算。设二叉树采用二叉链表存储，结点类型定义如下：typedef struct BtNode{ElemTypedata； ／*结点的数据域，ElemType的具体定义省略*／struct BtNode*ichiid，*rchild； ／*结点的左、右弦子指针域*／

题目

阅读下列说明和c函数代码，将应填入 (n) 处的字句写在答题纸的对应栏内。

【说明】

对二叉树进行遍历是二叉树的一个基本运算。遍历是指按某种策略访问二叉树的每个结点，且每个结点仅访问一次的过程。函数InOrder。()借助栈实现二叉树的非递归中序遍历运算。

设二叉树采用二叉链表存储，结点类型定义如下：

typedef struct BtNode{

ElemTypedata； ／*结点的数据域，ElemType的具体定义省略*／

struct BtNode*ichiid，*rchild； ／*结点的左、右弦子指针域*／

)BtNode，*BTree；

在函数InOrder()中，用栈暂存二叉树中各个结点的指针，并将栈表示为不含头结点

的单向链表(简称链栈)，其结点类型定义如下：

typedef struct StNode{ ／*链栈的结点类型*／

BTree elem； ／*栈中的元素是指向二叉链表结点的指针*／

struct StNode*link；

}S％Node；

假设从栈顶到栈底的元素为en、en-1、…、e1，则不含头结点的链栈示意图如图5—5

所示。

【C函数】

int InOrder(BTree root) ／*实现二叉树的非递归中序遍历*／

{

BTree ptr； ／*ptr用于指向二又树中的结点*／

StNode*q； ／*q暂存链栈中新创建或待删除的结点指针+／

StNode*stacktop=NULL； ／*初始化空栈的栈顶指针stacktop*／

ptr=root； ／*ptr指向二叉树的根结点*／

while( (1 ) I I stacktop!=NULL){

while(ptr!=NULL){

q=(StNode*)malloc(sizeof(StNode))；

if(q==NULL)

return-1；

q->elem=ptr；(2) ；

stacktop=q； ／*stacktop指向新的栈顶*／

ptr=(3 ) ； ／*进入左子树*／

}

q=stacktop； (4) ； ／*栈顶元素出栈*／

visit(q)； ／*visit是访问结点的函数，其具体定义省略*／

ptr= (5) ； ／*进入右子树*／

free(q)； ／*释放原栈顶元素的结点空间*／

}

return 0；

}／*InOrder*／

相似考题

1.遍历二叉树是指按照一定的规律走遍二叉树的每个结点,每个结点可能被访问多次。()此题为判断题(对，错)。

2.阅读以下说明和C语言函数，将应填入(n)处的字句写在答题纸的对应栏内。[说明]求树的宽度，所谓宽度是指在二叉树的各层上，具有结点数最多的那一层的结点总数。本算法是按层次遍历二叉树，采用一个队列q，让根结点入队列，若有左右子树，则左右子树根结点入队列，如此反复，直到队列为空。[函数]int Width ( BinTree *T{int front=-1, rear=-1; /*队列初始化*/int flag=0, count=0, p; /*p用于指向树中层的最右边的结点, flag 记录层中结点数的最大值*/if ( T!=Null){rear++;(1);flag=1;p=rear;}while ((2)){front++;T=q [front]];if (T->lchild!=Null ){roar+-+;(3);count++;}if ( T-＞rchild!=Null ){rear++; q[rear]=T-＞rchild;(4);}if (front==p ) // 当前层已遍历完毕{if((5))flag=count;count=0;p=rear, //p 指向下一层最右边的结点}}return ( flag );}

3.设计二叉树的双序遍历算法(双序遍历是指对于二叉树的每一个结点来说,先访问这个结点,再按双序遍历它的左子树,然后再一次访问这个结点,接下来按双序遍历它的右子树)。

4.下面是对二叉树的叙述，其中错误的是 （ ）A．二叉树的遍历是指不重复地访问二叉树中的所有结点B．二叉树的遍历允许重复地访问二叉树中的个别结点C．在遍历二叉树的过程中，一般先遍历左子树，然后再遍历右子树D．在先左后右的原则下，根据访问根结点的次序，二叉树的遍历可以分为三种：前序遍历、中序遍历、后序遍历

参考答案和解析
正确答案：(1)ptr! =NULL或ptr! =0或ptr(2)q->link=stacktop(3)ptr->lchild(4)stacktop=stacktop->link或stacktop=q->link(5)q->elem->rchild
(1)ptr! =NULL或ptr! =0或ptr(2)q->link=stacktop(3)ptr->lchild(4)stacktop=stacktop->link或stacktop=q->link(5)q->elem->rchild 解析：对非空二叉树进行中序遍历的方法是：先中序遍历根节点的左子树，然后访问根节点，最后中序遍历根节点的右子树。从以上算法的执行过程可知，从树根出发进行遍历时，递归调用InOrderTraversing(root-LeftChild)使得遍历过程沿着左孩子分支一直走向下层节点，直到到达二叉树中最左下方的节点(设为f)的空左子树为止，然后返回节点，再由递归调用InOrder Traversing(root->RightChild)进入f的右子树，并重复以上过程。在递归算法执行过程中，辅助实现递归调用和返回处理的控制栈实际上起着保存从根节点到当前节点的路径信息。用非递归算法实现二叉树的中序遍历时，可以由一个循环语句实现从指定的根节点m发，沿着左孩子分支一直到头(到达一个没有左子树的节点)的处理，从根节点到当前节点的路径信息(节点序列)可以明确构造一个栈来保存。
更多“ 阅读下列说明和c函数代码，将应填入 (n) 处的字句写在答题纸的对应栏内。【说明】对二叉树进行遍历是二叉树的一个基本运算。遍历是指按某种策略访问二叉树的每个结点，且每个结点仅访问一次的过程。函数InOrder。(”相关问题

  • 第1题：

    某二叉树前序遍历的结点访问顺序是abdgcefh，中序遍历的结点访问顺序是dgbaechf,则后序遍历的结点访问顺序是

    A．bdgcefha

    B．gdbecfha

    C．bdgaechf

    D．gdbehfca


    正确答案：A
    解析：由二叉树前序遍历序列和中序遍历序列可以唯一确定一棵二叉树。

  • 第2题：

    试题三（共 15 分）

    阅读以下说明和 C 程序，将应填入 （n） 处的字句写在答题纸的对应栏内。


    正确答案：

  • 第3题：

    所谓 ，即是按照某种次序，访问二叉树中的所有结点，使得每个结点被且仅被访问一次。


    A

  • 第4题：

    阅读下列函数说明和C函数，将应填入(n)处的字句写对应栏内。

    [说明]

    二叉树的二叉链表存储结构描述如下：

    typedef struct BiTNode

    { datatype data;

    struct BiTNode *lchild, * rchild; /*左右孩子指针*/

    }BiTNode,* BiTree;

    对二叉树进行层次遍历时，可设置一个队列结构，遍历从二叉树的根结点开始，首先将根结点指针入队列，然后从队首取出一个元素，执行下面两个操作：

    (1) 访问该元素所指结点；

    (2) 若该元素所指结点的左、右孩子结点非空，则将该元素所指结点的左孩子指针和右孩子指针顺序入队。

    此过程不断进行，当队列为空时，二叉树的层次遍历结束。

    下面的函数实现了这一遍历算法，其中Visit(datatype a)函数实现了对结点数据域的访问，数组queue[MAXNODE]用以实现队列的功能，变量front和rear分别表示当前队首元素和队尾元素在数组中的位置。

    [函数]

    void LevelOrder(BiTree bt) /*层次遍历二叉树bt*/

    { BiTree Queue[MAXNODE];

    int front,rear;

    if(bt= =NULL)return;

    front=-1;

    rear=0;

    queue[rear]=(1);

    while(front (2) ){

    (3);

    Visit(queue[front]-＞data); /*访问队首结点的数据域*/

    if(queue[front]—＞lchild!：NULL)

    { rear++;

    queue[rear]=(4);

    }

    if(queue[front]-＞rchild! =NULL)

    { rear++;

    queue[rear]=(5);

    }

    }

    }


    正确答案：(1) bt (2) ! =rear (3) front+ + (4) queue [front]-＞lchild (5) queue[front]-＞rchild
    (1) bt (2) ! =rear (3) front+ + (4) queue [front]-＞lchild (5) queue[front]-＞rchild 解析：(1)遍历开始时队列长度为1，其中只存放了根结点bt；
    (2)遍历过程是一个循环访问队列的过程，其终止条件是队列为空，即front等于rear；
    (3)遍历到某结点时，该结点应退出队列，因此队首元素的位置应该增1；
    (4)此处应将队首结点的左孩子结点放入队列，即插在队尾；
    (5)此处应将队首结点的右孩子结点放入队列，即插在队尾。

  • 第5题：

    阅读下列说明和?C++代码，将应填入(n)处的字句写在答题纸的对应栏内。
    【说明】
    阅读下列说明和?Java代码，将应填入?(n)?处的字句写在答题纸的对应栏内。
    【说明】
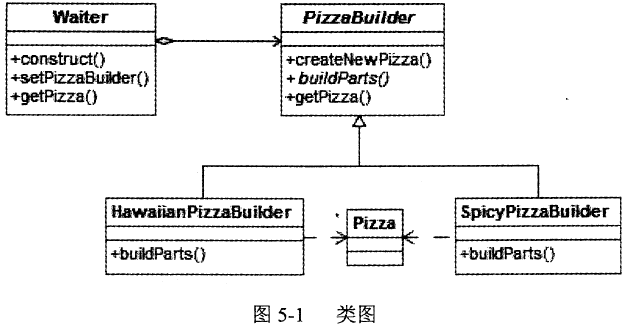
    某快餐厅主要制作并出售儿童套餐，一般包括主餐(各类比萨)、饮料和玩具，其餐品种
    类可能不同，但其制作过程相同。前台服务员?(Waiter)?调度厨师制作套餐。现采用生成器?(Builder)?模式实现制作过程，得到如图?6-1?所示的类图。






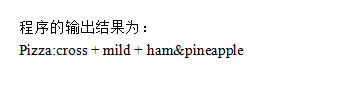    答案：
    解析：

相关内容