阅读下列函数说明和C代码,将应填入(n)外的字句写在对应栏内。[说明]为网球比赛的选手安排比赛日程。设有n(n=2m)位选手参加网球循环赛,循环赛共进行n-1天,每位选手要与其他n-1位选手赛一场,且每位选手每天赛一场,不轮空。设n位选手被顺序编号为1,2,…,n,比赛的日程表是一个n行n-1列的表,第i行j列的内容是第i号选手第j天的比赛对手。用分治法设计日程表,就是从其中一半选手(2m-1位)的比赛日程导出全体2m选手的比赛日程。从众所周知的只有两位选手的比赛日程出发,反复这个过程,直至为n位选手安排
题目
阅读下列函数说明和C代码,将应填入(n)外的字句写在对应栏内。
[说明]
为网球比赛的选手安排比赛日程。设有n(n=2m)位选手参加网球循环赛,循环赛共进行n-1天,每位选手要与其他n-1位选手赛一场,且每位选手每天赛一场,不轮空。
设n位选手被顺序编号为1,2,…,n,比赛的日程表是一个n行n-1列的表,第i行j列的内容是第i号选手第j天的比赛对手。用分治法设计日程表,就是从其中一半选手(2m-1位)的比赛日程导出全体2m选手的比赛日程。从众所周知的只有两位选手的比赛日程出发,反复这个过程,直至为n位选手安排好比赛日程为止。
如两位选手比赛日程表如下所示:

如四位选手比赛日程表如下所示:

函数中使用的预定义符号如下:
define M 64
int a[M+1][M];
[函数]
voidd main(){
int twoml,twom,i,j,m,k;
printf("指定n(=2的k次幂)位选手,请输入k:\n");
scanf("%d",&k);
/*8预设两位选手的比赛日程*/
a[1][1] =2;
a[2][1] =1;
m=1;
twoml=1;
while ( (1) ){
m++;
twoml+=twoml;
twom=twoml*2;/*为2^m位选手安排比赛日程*/
/*填日程表的左下角*/
for(i=twoml+1; (2) ;i++){
for(j=1; j<=twoml-1; j++){
a[i][j]=a[i-twoml][j]+twoml;
}
}
/*填日程表的右上角*/
a[1][twoml]= (3) ;/+填日程表右上角的第1列*/
for(i=2; i<=twoml; i++){
a[i][twoml]=a[i-1][twoml]+1;
}
/*填日程表右上角的其他列,参照前一列填当前列*/
for(j=twoml+1; j(twom;j++){
for(i=1; i a[i][j]= (4) ;
}
a[twoml][j]=a[1][j-1];
}
/*填日程表的右下角*/
for(j=twoml; j for(i=1;i<=twoml; i++){
a[ (5) [j]=i;
}
}
/*输出日程表*/
for(i=1; i<=twom; i++){
for(j=1;j printf("%4d",a[i][j]);
}
printf("\n");
}
printf("\n");
}
}
(1)
相似考题
参考答案和解析
mk 解析:题中已经说明该算法采用的是分治法,“就是从其中一半选手(2m-1位)的比赛日程导出全体2m选手的比赛日程”,再根据注释,不难确定空(1)应填mk。
更多“ 阅读下列函数说明和C代码,将应填入(n)外的字句写在对应栏内。[说明]为网球比赛的选手安排比赛日程。设有n(n=2m)位选手参加网球循环赛,循环赛共进行n-1天,每位选手要与其他n-1位选手赛一场,且每位选手每天”相关问题
-
第1题:
某单位职员在健身活动中举行乒乓球比赛,每个选手都要和其他选手各赛一场,一共120场比赛,则该单位参加人数是( )人。A.18
B.16
C.15
D.14答案:B解析:本题考查的是排列组合知识。假设总共有X人,因为每两个人要进行一场比赛,所以应该用组合公式: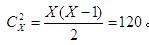 。此时利用代入排除法,只有X=16时满足条件。故正确答案为B。
。此时利用代入排除法,只有X=16时满足条件。故正确答案为B。 -
第2题:
某单位组织的羽毛球男单比赛共有48名选手报名参加,比赛采用淘汰赛制,在比赛中负一场的选手即被淘汰,直至决出最后的冠军。如每名选手每天最多参加一场比赛,则比赛至少需要举行几天?A.4
B.5
C.6
D.7答案:C解析:根据题意,每一轮的比赛都安排在一天,48=2 4 3,则4天后还剩3名选手,这3名选手还需要两场比赛才能决出冠军,所以比赛至少要举行4+2=6天。 -
第3题:
5.在有n个选手参加的单循环赛中,总共将进行()场比赛。
n(n-1)/2__ -
第4题:
象棋比赛中,每个选手都与其他选手恰好比赛一局,每局胜者记2分,负者记0分,和棋各记1分,四位观众统计了比赛中全部选手得分总数分别是:1979,1980,1983,1985,经核实只有一位观众统计正确,则这次比赛的选手共有多少名?A. 44
B. 45
C. 46
D. 47答案:B解析:很容易判断比赛总分不可能为奇数,则总分只可能是1980,那么由1980/2=990,所以共进行了990场比赛,设参赛选手为X,(x-1)+(x-2)+...+2+1=990,解得X=45,故答案为B。 -
第5题:
在网球双打比赛中,选手AB对CD,A选手首先发球,C选手选择接发球,那么在第二局比赛开始时,由()先发球,()接发球。
A.选手C先发球,选手A接发球
B.选手D先发球,选手B接发球
C.选手A先发球,选手C接发球
D.选手B先发球,选手D接发球
选手C先发球,选手A接发球
