一个具有767个结点的完全二叉树，其叶子结点个数为(62)。A．383B．384C．385D．386
题目
一个具有767个结点的完全二叉树，其叶子结点个数为(62)。
A．383
B．384
C．385
D．386
相似考题
更多“一个具有767个结点的完全二叉树,其叶子结点个数为(62)。A.383B.384C.385D.386 ”相关问题
-
第1题：
●一个具有767个结点的完全二叉树，其叶子结点个数为 (44) 。
(44) A．383
B．384
C．385
D．386
正确答案：B
【解析】可以根据公式进行推导，假设n0是度为0的结点总数(即叶子结点数)，n1是度为1的结点总数，n2是度为2的结点总数，由二叉树的性质可知：n0=n2+1，则n=n0+n1+n2(其中n为完全二叉树的结点总数)，由上述公式把n2消去得：n=2n0+n1-1，由于完全二叉树中度为1的结点数只有两种可能0或1，由此得到n0=(n+1)/2或n0=n/2，就可根据完全二叉树的结点总数计算出叶子结点数。本题计算结果为384。提示：该公式要记住，临时推导也可以，但容易耽误时间。 -
第2题：
一棵满二叉树中共有64个叶子结点,则其结点个数为()。A.64
B.65
C.127
D.128
参考答案：C
-
第3题：
一棵完全二叉树上有1001个结点，其中叶子结点的个数是(3)。
A．490
B．500
C．501
D．505
正确答案：C
解析：这棵完全--X．树的高度为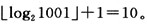
根据二叉树的性质，从第1层到第 9层共有结点29-1＝511个。第10层全部是叶子结点，因此处于第10层的叶子结点数为 1001-511＝490。同时注意到，第9层有29-1-490/2＝11个叶子结点。因此共有490+11 =501个叶子结点。也可以用另外一种方法来做。设二叉树的总结点数为n，叶子结点数为n0，度为1的结点数为n1，度为2的结点数为n2，根据二叉树的性质有：n0=n2+1，n=n1+2n2+1，于是可得，n=n1+2n0-1，由于在完全二叉树中，度为1的结点总数n1要么为0要么为1，此题中显然为0，这样才能保证等式两边都是奇数，因此1001＝2n0-1，解得n0＝501。
-
第4题：
一个具有767个结点的完全二叉树，其叶子结点个数为(32)。
A．382
B．387
C．384
D．388
正确答案：C
解析：可以根据公式进行推导，假设n。是度为0的结点总数(即叶子结点数)，n1是度为1的结点总数，n2是度为2的结点总数，由二叉树的性质可知：n=n0+n1+n2(其中n为完全二叉树的结点总数)，n=n1+2×n2+1(树的分支对应一个非根结点)；由两公式得：n0=n2+1。由上述公式把n2消去得：n=2n0+n1-1，由于完全二叉树中度为1的结点数只有两种可能0或1，由此得到767=2n0+n1-1，其中n1=『0，1』。可以发现由于n0为整数，所以n1=0，本题计算得：384。 -
第5题：
一棵完全二叉树上有1001个结点.其中叶子结点的个数是()。A.250
B.500
C.505
D.501答案：D解析：
-
第6题：
具有5个叶子结点的二叉树中，度为2的结点的个数为()。A.4
B.6
C.5
D.不确定答案：A解析：二叉树的性质1：非空二叉树上叶结点数等于双分支结点数加1。因此度为2的结点的个数为5-1=4。 -
第7题：
具有100个结点的完全二叉树的叶子结点数为（）。
正确答案:50 -
第8题：
深度为k的完全二叉树至少有（）个结点，至多有（）个结点，具有n个结点的完全二叉树按层序从1开始编号，则编号最小的叶子的序号是（）。
正确答案:2k-1；2k-1；2k-2+1 -
第9题：
设一棵完全二叉树具有1000个结点，则此完全二叉树有（）个叶子结点，有（）个度为2的结点，有（）个结点只有非空左子树，有（）个结点只有非空右子树。
正确答案:500；499；1；0 -
第10题：
填空题在含100个结点的完全二叉树，叶子结点的个数为（）。正确答案： 50解析： 暂无解析 -
第11题：
填空题一个具有767个结点的完全二叉树，其叶子结点个数为（）。正确答案： 384解析： 暂无解析 -
第12题：
单选题深度为7的完全二叉树中共有125个结点，则该完全二叉树中的叶子结点数为（ ）。A62
B63
C64
D65
正确答案： B解析：
定义一棵树的根结点所在的层次为1，其他结点所在的层次等于它的父结点所在的层次加1，树的最大层次称为树的深度。完全二叉树指除最后一层外，每一层上的结点数均达到最大值，在最后一层上只缺少右边的若干结点。本题中，前6层是满二叉树，结点个数为26-1=63，所以第7层有125-63=62个叶子结点，分别挂在第6层的左边62个结点上，所以第6层的最后1个结点为叶子结点，该完全二叉树共有62+1=63个叶子结点。答案选择B选项。 -
第13题：
一个具有767个节点的完全二叉树，其叶子节点个数为(18)。
A．383
B．384
C．385
D．386
正确答案：B
解析：设二叉树中总节点数，以及度为0、度为1和度为2的节点数分别为n，n0，n1和n2，依据二叉树的性质可得到下列等式：n=n0+n1+n2n=768n-1=n1+2n2通过化简可得到769=2n0+n1在完全二叉树中，度为1的节点要么没有，要么有1个。上面等式左边为一个奇数，等式右边2n0是一个偶数，要使等式成立，n1只能为奇数，即是1，所以叶子节点个数n0=384。 -
第14题：
已知一棵含50个结点的二叉树中只有一个叶子结点，则该树中度为1的结点个数为( )
A．O
B．1
C．48
D．49
正确答案：D
解析：由此二叉树仅有一个叶子结点，可知此二叉树中除叶子结点外的所有结点都仅有一颗子树，即这些结点的度都为1，而这些结点的个数为50-1=49。 -
第15题：
一个具有767个结点的完全二叉树，其叶子结点个数为(33)。
A．383
B．384
C．385
D．386
正确答案：B
解析：完全二叉树中第1层1个结点，第2层2个结点，第3层4个结点，第k层2k-1个结点。共1+2+4+…+2k-1=2k-1=n；k=log2(n+1)=log2768=9.6，此树共10层，第9层有28=256个结点，前9层有29-1=511，第10层有767-511=256个结点，需要128个父结点，因此这棵完全二叉树叶子结点个数为：(256-128)+256=384。 -
第16题：
在深度为5的完全二叉树中，叶子结点的个数最多为【1】。
正确答案：
16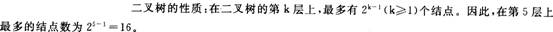
-
第17题：
某高度为k的完全二叉树中，所含叶子结点的个数最少为()。
答案：C解析：
-
第18题：
具有n个结点的完全二叉树若按层次从上到下，从左到右对其编号（根结点为1），则编号最大的分支结点序号是（），编号最小的分支结点序号是（），编号最大的叶子结点序号是（），编号最小的叶子结点序号是（）
正确答案:[n/2]；1；n；[n/2]+1 -
第19题：
一个具有767个结点的完全二叉树，其叶子结点个数为（）。
正确答案:384 -
第20题：
在含100个结点的完全二叉树，叶子结点的个数为（）。
正确答案:50 -
第21题：
填空题具有n个结点的完全二叉树若按层次从上到下，从左到右对其编号（根结点为1），则编号最大的分支结点序号是（），编号最小的分支结点序号是（），编号最大的叶子结点序号是（），编号最小的叶子结点序号是（）正确答案： [n/2],1,n,[n/2]+1解析： 暂无解析 -
第22题：
填空题具有100个结点的完全二叉树的叶子结点数为（）。正确答案： 50解析： 100个结点的完全二叉树中最后一个结点的编号为100，其双亲即最后一个分支结点的编号为50，也就是说，从编号51开始均为叶子。 -
第23题：
填空题设一棵完全二叉树具有1000个结点，则此完全二叉树有（）个叶子结点，有（）个度为2的结点，有（）个结点只有非空左子树，有（）个结点只有非空右子树。正确答案： 500,499,1,0解析： 暂无解析