阅读下列程序说明和C代码,将应填入(n)处的字句写在对应栏内。【说明】“背包问题”的基本描述是:有一个背包,能盛放的物品总重量为S,设有N件物品,其重量分别为w1,w2,…,wn。希望从N件物品中选择若干件物品,所选物品的重量之和恰能放入该背包,即所选物品的重量之和等于S。如下程序均能求得“背包问题”的一组解,其中程序1是“背包问题”的递归解法,而程序2是“背包问题”的非递归解法。【程序1】include<stdio.h>define N 7define S 15int w[N+1]={0,1,4,3,4
题目
阅读下列程序说明和C代码,将应填入(n)处的字句写在对应栏内。
【说明】
“背包问题”的基本描述是:有一个背包,能盛放的物品总重量为S,设有N件物品,其重量分别为w1,w2,…,wn。希望从N件物品中选择若干件物品,所选物品的重量之和恰能放入该背包,即所选物品的重量之和等于S。
如下程序均能求得“背包问题”的一组解,其中程序1是“背包问题”的递归解法,而程序2是“背包问题”的非递归解法。
【程序1】
include<stdio.h>
define N 7
define S 15
int w[N+1]={0,1,4,3,4,5,2,7};
int knap(int s, int n)
{
if(s==0) return 1;
if(s<0 || (s>0 && n<1))return 0;
if((1)){/*考虑物品n被选择的情况*/
printf("%4d",w[n]);
return 1;
}
return (2);/*考虑不选择物品n的情况*/
}
main()
{
if(knap(S,N))printf("OK!\n");
else printf("N0!\n");
}
【程序2】
include<stdio.h>
define N 7
define S 15
typedef struct{
int s;
int n;
int job;
}KNAPTP;
int w[N+1]={0,1,4,3,4,5,2,7};
int knap(int s, int n);
main()
{
if(knap(S,N)) printf("0K!\n");
else printf("N0!\n");
}
int knap(int s, int n)
{
KNAPTP stack[100],x;
int top, k, rep;
x.s=s;x.n=n;
x.job=0;
top=1; stack[top]=x;
k=0;
while( (3) ){
x=stack[top];
rep=1;
while(!k && rep){
if(x.s==0) k=1;/*已求得一组解*/
else if(x.s<0 || x.n<=0) rep=0;
else{
x.s=(4);
x.job=1;
(5)=x;
}
}/*while*/
if(!k){
rep=1;
while(top>=1 && rep){
x=stack[top--];
if(x.job==1){
x.s +=w[x.n+1];
x.job=2;
stack[++top]=x;
(6);
}/*if*/
}/*while*/
}/*if*/
/*while*/
if(k){&nbs
相似考题
参考答案和解析
(1) knap(s-w[n],n-1) (2) knap(s,n-1) (3) top>=1 && !k 或 top>0 && k==0 (4) x.s-w[x.n--] (5) stack[++top] (6) rep=0 解析:本题考查“背包”问题,这是一个非常经典的问题,一般采用递归法实现。
典型做法是逐个考查每一件物品,对于第i件物品的选择考虑有两种可能。
.考虑物品i被选择,这种可能仅当包含它不会超过方案总重量限制时才是可行的。选中后继续递归考虑其余物品的选择。
.考虑物品i不被选择,这种可能仅当不包含物品i也有可能找到价值更大的方案时才是可行的。
程序1是递归算法实现。对每个物品i,考查选择放入和不放入背包两种情况。函数knap(int s,int n)中,形参s是考查完物品i后背包还能装载的重量,n是考查完物品i后下一个待考查的物品。每次选择一个物品放入背包,那么剩余的物品和背包剩余重量又构成一个“背包问题”。根据注释,空(1)是考查物品n放入背包的情况,既然放入背包,则背包剩余可装重量为 s-w[n],继续考查物品n-1。这点可从主函数的调用形式“knap(S,N)”分析出。故空(1)应填“knap(s-w[n],n-1)”。空(2)是考查物品n不放入背包的情况,既然不放入背包,则背包可装重量仍为s,继续考查物品n-1。故空(2)应填“knap(s,n-1)”。
程序2是非递归算法实现,相对较难。算法思想仍是对每个物品i分别考查选择放入和不放入两种情况,借助栈实现,即数组stack。其实就是手动完成递归算法中由系统自动完成的压栈、出栈操作。
据注释“k=1时则求得一组解”可知k为是否求得解的标志:k=0表示没有解,继续求解。经分析,结构变量KNAPTP表示经过考查的物品:分量s表示考查过该物品后,背包所能盛放的物品的重量,分量n表示待考查的下一个物品在数组w中的下标,分量job表示物品当前的状态,job等于1表示物品n可以放入背包,job等于2表示物品不能放入背包,在以后的选取中将不再考虑该物品,初始时job等于0表示背包中没有放入任何物品。rep是一个标志变量,等于。表示结束当前的动作,等于1表示继续进行当前的动作;当栈顶物品不能装入背包时,将rep置为0,表示下一步不再从数组w中取物品。rep初值为1。x为工作节点。
while( (3) )循环体内的语句可以肯定是考查各个物品n的选择情况。对物品n,先考查将物品放入背包的情况。显然,如果物品n满足放入背包的条件,则空(4)和空(5)完成将物品放入背包的操作,其中空(4)应该是将工作节点x的分量s值减去所考查物品的重量。且n要减1,修改背包可容纳物品的重量和设置下一个待考查物品。而空(5)则需要将修改后的工作节点x送到栈顶,将下一个待考查的物品入栈。故空(4)应填“x.s-w[x.n--]”,空(5)应填“stack[++top]”。
if(!k)后的程序段是处理所考查的物品不满足放入背包的条件时的情况(rep=0,while(!k && rep)循环结束),则将该物品从背包中取出,修改其job值为2,用以标记该物品不能放入背包。修改完后跳出while(top>=1 && rep)循环,因此需要将rep置为0,用以结束循环。故空(6)应填“rep=0”。
更多“阅读下列程序说明和C代码,将应填入(n)处的字句写在对应栏内。 【说明】 “背包问题”的基本描述是:有 ”相关问题
-
第1题:
●试题二
阅读下列函数说明和C代码,将应填入(n)处的字句写在答题纸的对应栏内。
【说明】
该程序运行后,输出下面的数字金字塔

【程序】
include<stdio.h>
main ()
{char max,next;
int i;
for(max=′1′;max<=′9′;max++)
{for(i=1;i<=20- (1) ;++i)
printf(" ");
for(next= (2) ;next<= (3) ;next++)
printf("%c",next);
for(next= (4) ;next>= (5) ;next--)
printf("%c",next);
printf("\n");
}
}
正确答案:
●试题二【答案】(1)(max-′0′)(2)′1′(3)max(4)max-1(5)′1′【解析】该程序共有9行输出,即循环控制变量max的值是从1~9。每行输出分3部分,先用循环for语句输出左边空白,(1)空填"(max-′0′)";再用循环输出从1到max-′0′的显示数字,即(2)空和(3)空分别填1和max;最后输出从max-′1′~1的显示数字,即(4)空和(5)空分别填和max-1和′1′。 -
第2题:
阅读下列说明和C++-代码,将应填入(n)处的字句写在答题纸的对应栏内。 【说明】 某发票(lnvoice)由抬头(Head)部分、正文部分和脚注(Foot)部分构成。现采用装饰(Decorator)模式实现打印发票的功能,得到如图5-1所示的类图。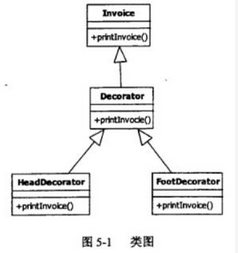
【C++代码】 #includeusing namespace std; class invoice{ public: (1){ cout<<"This is the content of the invoice!"< 答案:解析:(1) virtual void printInvoice() (2) ticket->printInvoice() (3) Decorator::printInvoice() (4) Decorator::printInvoice() (5) &a
【解析】
试题分析
1.Invoice类下,义虛函数,按类图,函数名是printInvoice
2.前面定义对象名是ticket,那么在ticket不为空的时候调用函数printInvoice
3.这部分填写发票的抬头,看类图应该实现函数printInvoice ,Decorator装饰模式使用该方法
4.这部分是发票的脚注,看类图应该实现函数printlnvoice,Decorator装饰模式使用该方法
5.FootDecorator a(NULL) ;脚步的装饰参数是a,调用a参数,第3题:
阅读下列说明和Java代码,将应填入(n)处的字句写在答题纸的对应栏内。【说明】 某文件管理系统中定义了类OfficeDoc和DocExplorer,当类OfficeDoc发生变化时,类DocExplorer的所有对象都要更新其自身的状态,现采用观察者(Observer)设计模式来实现该需求,所设计的类图如图6-1所示。
 答案:解析:1: void update()2: Observer3: obs.update()4: Subject5: Attach(this)
答案:解析:1: void update()2: Observer3: obs.update()4: Subject5: Attach(this)第4题:
试题三(共 15 分)
阅读以下说明和 C 程序,将应填入 (n) 处的字句写在答题纸的对应栏内。
 正确答案:
正确答案:
第5题:
阅读下列说明和C++代码,回答问题,将解答填入答题纸的对应栏内。
【说明】某航空公司的会员积分系统将其会员划分为:普卡 (Basic)、银卡(Silver)和金卡 (Gold) 三个等级。非会员 (NonMember) 可以申请成为普卡会员。会员的等级根据其一年内累积 的里程数进行调整。描述会员等级调整的状态图如图 5-1 所示。现采用状态 (State) 模式实现上述场景,得到如图 5-2 所示的类图。
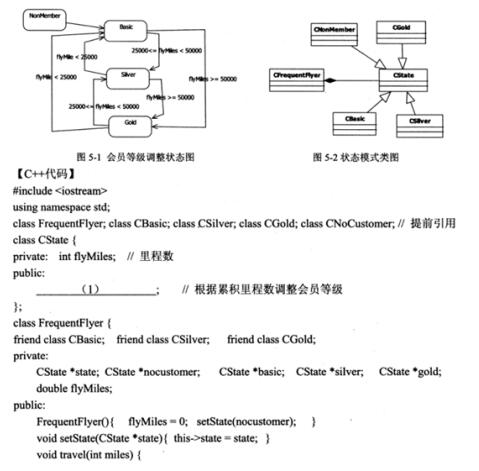

【问题1】(15分)阅读上述说明和C++代码,将应填入 (n) 处的字句写在答题纸的对应栏内。答案:解析:注意:原版的题目应该是Cbasic、CSilve。(1) virtual double travel(int miles,FrequentFlyer* context)=0(2)context->setState(context->Cbasic)(3)context->setState(context->CSilve)(4)context->setState(context->Cbasic)(5)context->setState(context->CSilve)第6题:
阅读下列说明和?C++代码,将应填入(n)处的字句写在答题纸的对应栏内。
【说明】
阅读下列说明和?Java代码,将应填入?(n)?处的字句写在答题纸的对应栏内。
【说明】
某快餐厅主要制作并出售儿童套餐,一般包括主餐(各类比萨)、饮料和玩具,其餐品种
类可能不同,但其制作过程相同。前台服务员?(Waiter)?调度厨师制作套餐。现采用生成器?(Builder)?模式实现制作过程,得到如图?6-1?所示的类图。
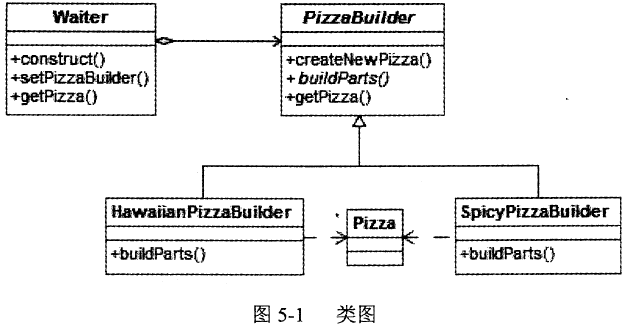


 答案:解析:
答案:解析:
