己知某带权图G的邻接表如下所示,其中表结点的结构为:则图G是______。A.无向图B.完全图C.有向图D.强连通图
题目
己知某带权图G的邻接表如下所示,其中表结点的结构为:
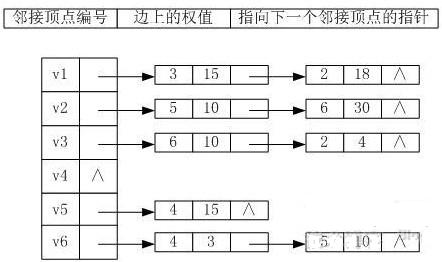
则图G是______。
A.无向图
B.完全图
C.有向图
D.强连通图
相似考题
更多“ 己知某带权图G的邻接表如下所示,其中表结点的结构为:则图G是______。A.无向图B.完全图C.有向图D.强连通图 ”相关问题
-
第1题:
已知某带权图G的邻接表如下所示,其中表结点的结构为: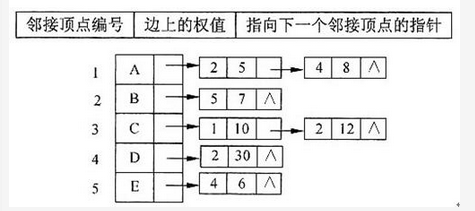
以下关于该图的叙述中,正确的是( )。A.图G是强连通图
B.图G具有14条弧
C.顶点B的出度为3
D.顶点B的入度为3答案:D解析:本题考查数据结构基础知识。
从题图中可知,顶点A、B、C、D、E的编号为1~5,因此顶点A的邻接表中的两个结点表示:存在顶点A至顶点B的弧且权值为5,存在顶点A至顶点D的弧且权值为8,再考查顶点B只有一个邻接顶点E,因此该图为有向图,有7条弧,如下图所示。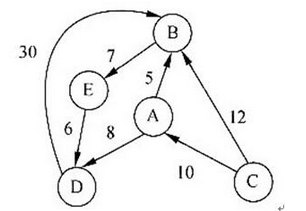
若在有向图中,每对顶点之间都存在路径,则是强连通图。上图不是强连通图,例如,顶点C至B有路径,反之则没有路径。在有向图中,顶点的入度是以该顶点为终点的有向边的数目,而顶点的出度指以该顶点为起点的有向边的数目。对于顶点B,其出度为1,而入度为3。 -
第2题:
图G的邻接矩阵如下图所示(顶点依次表示为v0、v1、v2、v3、v4、v5),G是(请作答此空)。对G进行广度优先遍历(从v0开始),可能的遍历序列为( )。
 A.无向图
A.无向图
B.有向图
C.完全图
D.强连通图答案:B解析: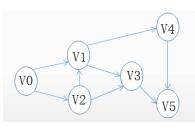
-
第3题:
【单选题】在简单无向图G = (V, E) 中,如果V中的每个结点都与其余的所有结点邻接,则该图称为()。
A.连通图
B.强连通图
C.完全图
D.平凡图。
G 中有一条从vj到vi的路径 -
第4题:
某图的邻接矩阵如下,该图为(请作答此空);若采用邻接表表示该图,则邻接表中用来表示边(或弧)的表结点总数为( )个。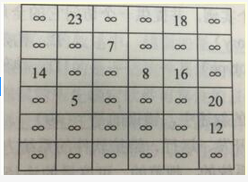 A.无向图
A.无向图
B.有向图
C.完全图
D.二部图答案:B解析:图的邻接矩阵是一个方阵,所有行标和列标都与图中的顶点一一对应,这样对于矩阵中的一个元素 [i,j],其值为1 表示 i、j 对应的顶点间有边(或弧),其值为 0则表示 i、j对应的顶点间不存在边(或弧)。显然,图中总共有9条边。在无向图中,边 (i,j)与(j,i)是指同一条边,其取值是相同的;在有向图中,与 是两条不同的弧。而在本题中,矩阵中的(i,j)与(j,i)是不同的,因此这个是有向图。 -
第5题:
已知某带权图G的邻接表如下所示,其中表结点的结构为:
则图G是( )。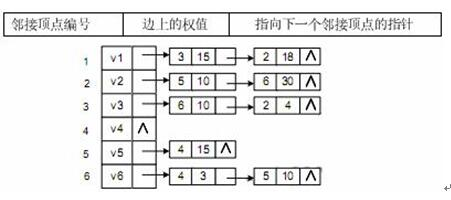 A.无向图
A.无向图
B.完全图
C.有向图
D.强连通图答案:C解析:本题考查数据结构基础知识。
从题中的邻接表中可知,该图的边为、 、 、 、 、 、 、 、 ,如下图所示,显然,这是个有向图。
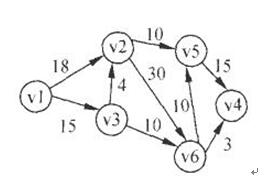
在无向图中,若存在边(vi,vj),则它同时为vj和vi之间的边。在上面的邻接表中,存在边,而不存在 ,因此该图不是无向图。
对于无向图,其边数e和顶点数n的关系为e=n×(n-1)/2。对于有向图,其边数e和顶点数n的关系为e = n×(n-1),因此该图不是完全图。
若有向图为强连通图,则任意两个顶点间要存在路径。在该有向图中,由于顶点v4没有出边,因此,不存在v4到其他顶点的路径,因此该图不是强连通图。
