●从任意初始值XO开始，通过迭代关系式Xn=Xn-1/2+1(n=1，2，…)，可形成序列X1，X2，…。该序列将收敛于(65)。(65)A．1/2B.1C．3/2D．2
题目
●从任意初始值XO开始，通过迭代关系式Xn=Xn-1/2+1(n=1，2，…)，可形成序列X1，X2，…。该序列将收敛于(65)。
(65)A．1/2
B.1
C．3/2
D．2
相似考题
更多“●从任意初始值XO开始,通过迭代关系式Xn=Xn－1／2＋1(n=1,2,…),可形成序列X1,X2,…。该序列将收敛于(65 ”相关问题
-
第1题：
设X1,X2,…,Xn,…相互独立,则X1,X2,…,Xn,…满足辛钦大数定律的条件是( )
A.X1,X2,…,Xn,…同分布且有相同的数学期望与方差
B.X1,X2,…,Xn,…同分布且有相同的数学期望
C.X1,X2,…,Xn,…为同分布的离散型随机变量
D.X1,X2,…,Xn,…为同分布的连续型随机变量答案：B解析：根据辛钦大数定律的条件，应选(B). -
第2题：
已知样本x1,x2,…,xn，其中μ未知。下列表达式中，不是统计量的是（）。
A. X1 +X2 B. max(x1,x2,…,xn)
C. X1 +X2 -2μ D. (X1 -μ)/σ
E. X1 +μ答案：C,D,E解析：不含未知参数的样本函数称为统计量。CDE三项都含有未知数μ，不是统计量。 -
第3题：
设总体X服从参数为2的指数分布，X1，X2，…，Xn为来自总体X的简单随机样本，则当n→∞时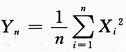
，依概率收敛于_______.答案：解析：本题是数三的考题，根据切比雪夫大数定律或者辛钦大数定律
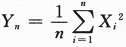，依概率收敛于
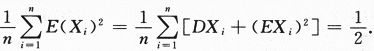答案应填
-
第4题：
设总体X服从正态分布N(μ，σ^2)(σ>0)，从该总体中抽取简单随机样本X1，X2，…，Xn(n≥2)，其样本均值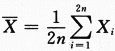
,求统计量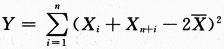
的数学期望E(Y).答案：解析：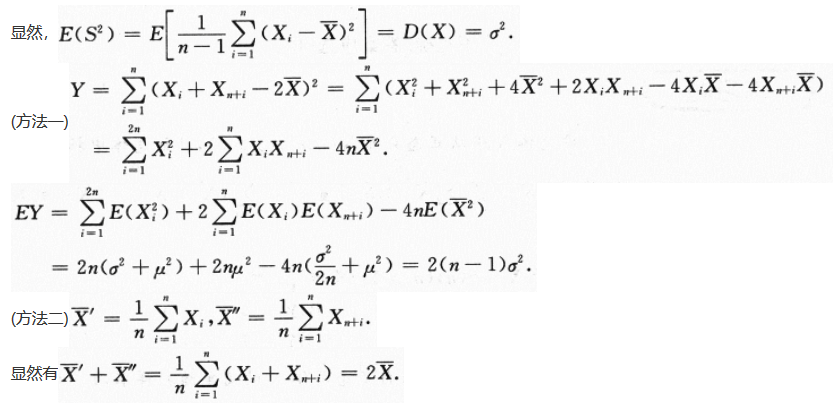
-
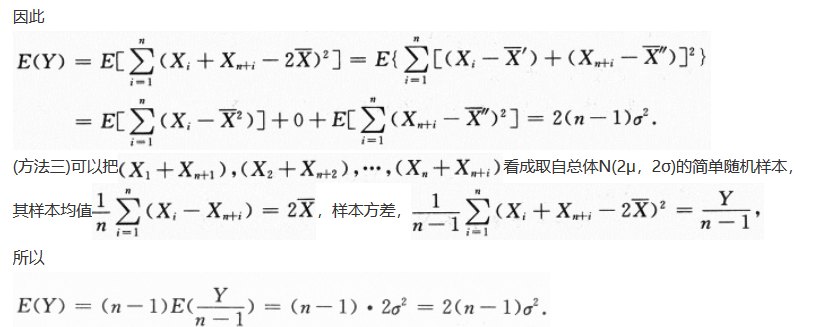
第5题：
设X1,2X,…,Xn（n>2）相互独立且都服从N(0,1),Yi=Xi-X（i=1,2,…,n）.求：
(1)D(Yi)(i=1,2,…,n);(2)Cov(Y1,Yn);(3)P(Yn+Yn≤0).答案：解析：
-
第6题：
从均值为μ、方差为σ2的总体中抽得一个容量为n的样本X1，X2，…，Xn，其中μ已知，σ2未知，下列各项属于统计量的有（ ）。
答案：A,B,C解析：统计量是不含未知参数的样本函数，因此DE两项不是统计量。 -
第7题：
若Ad-I=0，那么d是由Z2上n阶线性常系数齐次递推关系式产生的什么序列周期？（）
- A、不存在这样的序列
- B、任意序列
- C、项数小于3的序列
- D、项数等于7的序列
正确答案:B -
第8题：
单选题已知序列X={x1，x2，…，xm}，序列Y={y1，y2，…，yn}，使用动态规划算法求解序列X和Y的最长公共子序列，其最坏时间复杂度为（）。AO（m*n）
BO（m+n）
CO（m*2n）
DO（n*2m）
正确答案： A解析： 暂无解析 -
第9题：
问答题设总体X～N(μ,σ2)，x1,x2,…xn为其样本，为样本均值,则____．正确答案：解析： -
第10题：
单选题若Ad-I=0，那么d是由Z2上n阶线性常系数齐次递推关系式产生的什么序列周期？（）A不存在这样的序列
B任意序列
C项数小于3的序列
D项数等于7的序列
正确答案： D解析： 暂无解析 -
第11题：
问答题设函数f（x）在（a，b）内连续，a＜x1＜x2＜…＜xn＜b，证明：必∃ξ∈（a，b），使f（ξ）＝[f（x1）＋f（x2）＋…＋f（xn）]/n。正确答案：
设f(x)在[x1,xn]上的最大值为M,最小值为m。
则由题设可知,f(x)在[x1,xn]上连续,则它在[x1,xn]上必有最大值和最小值,则m≤[f(x1)+f(x2)+…+f(xn)]/n≤M。
由最值介值定理可知,必∃ξ∈[x1,xn]⊂(a,b),使得f(ξ)=[f(x1)+f(x2)+…+f(xn)]/n。解析： 暂无解析 -
第12题：
问答题设X1，X2，…，Xn相互独立且同服从分布B（1，p），Z＝X1＋X2＋…＋Xn，证明Z～B（n，p）。正确答案：
利用数学归纳法。
当k=2时,X1+X2=Z~B(2,p)。
假设当k=n-1时,X1+X2+…+Xn-1=Z1~B(n-1,p)。
则当k=n时,Z=(X1+X2+…+Xn-1)+Xn=Z1+Xn,Z~B(n-1+1,p),即Z~B(n,p)。解析： 暂无解析 -
第13题：
从正态总体X～N（0,σ^2）中抽取简单随机样本X1,X2,…,Xn,则可作为参数σ^2的无偏估计量的是().
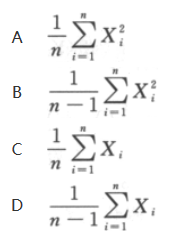答案：A解析：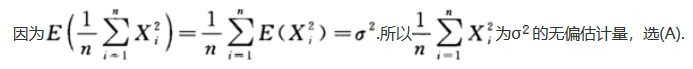
-
第14题：
设X1,X2,…Xn是简单随机样本，则有（ ）。
A. X1,X2,…Xn相互独立 B. X1,X2,…Xn有相同分布
C. X1,X2,…Xn彼此相等 D.X1与(X1,+X2)/2同分布
E.X1与Xn的均值相等答案：A,B,E解析：简单随机样本满足随机性和独立性，且每一个样本都与总体同分布，样本均值相等。 -
第15题：
设X1,X2,…,Xn（n>2）是来自总体X～N(0,1)的简单随机样本,记Yi=Xi-
（i=1,2,…,n）.求：(1)D(Yi);(2)Cov(Yb,Yn).答案：解析：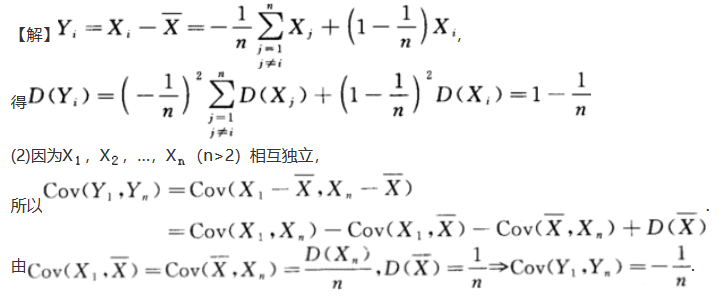
-
第16题：
若随机变量x1,x2,…,xn相互独立同分布于N{μ,2^2},则根据切比雪夫不等式得P{｜x－μ｜≥2）≤_______.答案：解析：因为X1，X2…，Xn相互独立同分布于N（μ，2^2），所以
，从而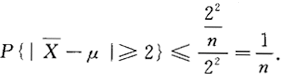
-
第17题：
设总体X~N(0,σ2)，X1，X2，...Xn是自总体的样本，则σ2的矩估计是:
答案：D解析：提示 注意 E(x)=0，σ2=D(x)=E(x2) - [E(x)]2=E(x2)，σ2也是x的二阶原点矩，σ2的矩估计量是样本的二阶原点矩。 -
第18题：
设进行线性卷积的两个序列x1(n)和x2(n)的长度分别为M和N，在什么条件下它们的循环卷积结就是线性卷积？
正确答案: 在它们的后面添加零，使它们成为长度L＝M+N-1的序列，再求它们的L点的循环卷积，结果序列长度为L。则循环卷积结果就是线性卷积。 -
第19题：
设X1，X2，…，Xn是从总体X中抽取的容量为n的一个样本，如果由此样本构造一个函数T（X1，X2，…，Xn），不依赖于任何未知参数，则函数T（X1，X2，…，Xn）是一个（）
正确答案:统计量 -
第20题：
多选题设随机变量X仅取n个值x1, x2,… xn,其概率函数为P(X=xi)=pi，则( )。A-1≦pi≦1,i=1,2…,n
Bpi≧0,i=1,2,…,n
Cp1+p2+…+Pn≦1
Dp1+p2+…+Pn=1
正确答案： B,A解析： 暂无解析 -
第21题：
问答题总体x～N(μ，σ2)，x1,x2,…，xn为其样本，未知参数μ的矩估计为_______ .正确答案：解析： -
第22题：
问答题设A为n阶方阵，若对任意n维向量x(→)＝（x1，x2，…，xn）T都有Ax(→)＝0。证明：A＝0。正确答案：
由对任意n维向量x都有Ax=0,知对基本单位向量组ε1,ε2,…,εn,Aεi=0(i=1,2,…,n)成立。
所以有A(ε1,ε2,…,εn)=0,即AE=0,故A=0。解析： 暂无解析 -
第23题：
问答题设A为n阶方阵，若对任意n维向量X=（x1，x2，…，xn）T都有AX=0.证明：A=0.正确答案：
证明:由对任意n维向量X都有AX=0,知对基本单位向量组ε1,ε2,…,εn,Aεi=0(i=1,2,…,n)成立.
所以有A(ε1,ε2,…,εn)=0,即AE=0,故A=0.解析： 暂无解析