菲波那契(Fibonacci)数列定义为 f(1)=1,f(2)=1,n>2时f(n)=f(n-1)+f(n-2) 据此可以导出,n>1时,有向量的递推关系式: (f(n+1),f(n))=f(f(n),f(n-1))A 其中A是2*2矩阵( )。从而,(f(n+1),f(n)=(f(2),f(1))*( )A.B.C.D.A.An-1B.AnC.An+1D.An+2
题目
菲波那契(Fibonacci)数列定义为 f(1)=1,f(2)=1,n>2时f(n)=f(n-1)+f(n-2) 据此可以导出,n>1时,有向量的递推关系式: (f(n+1),f(n))=f(f(n),f(n-1))A 其中A是2*2矩阵( )。从而,(f(n+1),f(n)=(f(2),f(1))*( )
A. B.
B. C.
C. D.
D. A.An-1B.AnC.An+1D.An+2
A.An-1B.AnC.An+1D.An+2
相似考题
更多“菲波那契(Fibonacci)数列定义为 f(1)=1,f(2)=1,n>2时f(n)=f(n-1)+f(n-2) 据此可以导出,n& ”相关问题
-
第1题:
已知f(1)=1,f(2)=2,当n≥3时,f(n)= f(n-1)+f(n-2),编程求f(100)的值,应选择的算法为( )
A.解析法
B.穷举法
C.递归法
D.冒泡排序法
正确答案:C
-
第2题:
下面的程序是求菲波那契(Fibonacci)数列的前10项。已知该数列的前两项都为1,即F(1)=1,F(2)=1;而后面各项满足: F(n)=F(n-1)+F(n-2)。请在程序的每条横线处填写一条语句,使程序的功能完整。
注意:请勿改动main()主方法和其他已有的语句内容,仅在横线处填入适当的语句。
public class Fibonacci{
public static void main(String args[]){
System.out.printtn("Fibonacci is"+" "+"_______________________);
}
static long fib(int n){
if(______________)
return 1;
else
return _________________
}
}
正确答案:fib(10) n==0||n==1 fib(n-1)+fib(n-2);
fib(10) n==0||n==1 fib(n-1)+fib(n-2); 解析:本题主要考查递归算法。解答本题的关键是理解递归算法的思想。在本题中,fib(10)方法是计算含由10项的菲波那契 (Fibonacci)数列,而fib(n-1)+fib(n-2);是用来计算第0项和第1项以外的菲波那契(Fibonacci)数列。 -
第3题:
请编写函数fun(),它的功能是求Fibonacci数列中小于t的最大的一个数,结果由函数返回。其中Fibonacci数列F(n)的定义为
F(0)=0,F(1)=1
F(n)=F(n-1)+F(n-2)
例如:t=1000时,函数值为987。
注意:部分源程序给出如下。
请勿改动主函数main和其他函数中的任何内容,仅在函数fun的花括号中填入所编写的若干语句。
试题程序:
include <conio.h>
include <math.h>
include <stdio.h>
int fun(int t)
{
}
main()
{
int n;
clrscr();
n=1000;
printf("n=%d, f=%d\n",n, fun(n));
}
正确答案:int fun(int t) { int a=1b=1c=0i; /*a代表第n-2项b代表第n-1项c代表第n项*/ /*如果求得的数。比指定比较的数小则计算下一个Fibonacci数对ab得新置数*/ do { c=a+b; a=b; b=c; } while(ct); /*如果求得的数c比指定比较的数大时退出循环*/ c=a; /*此时数c的前一个Fibonacci数为小于指定比较的数的最大的数*/ return c; }
int fun(int t) { int a=1,b=1,c=0,i; /*a代表第n-2项,b代表第n-1项,c代表第n项*/ /*如果求得的数。比指定比较的数小,则计算下一个Fibonacci数,对a,b得新置数*/ do { c=a+b; a=b; b=c; } while(ct); /*如果求得的数c比指定比较的数大时,退出循环*/ c=a; /*此时数c的前一个Fibonacci数为小于指定比较的数的最大的数*/ return c; } 解析:根据所给数列定义不难发现,该数列最终的结果是由两个数列之和组成,所以可以在循环内部始终把c看成是前两项之和(即第n项),而a始终代表第n-2项,b始终代表第n-1项(通过不断地重新赋值来实现)。应注意,退出循环时得到的数c是大于指定比较的数的最小的数,而它的前一个数就是小于指定比较的数的最大的数。 -
第4题:
编写函数jsValue(),它的功能是求Pibonacci数列中大于t的最小的一个数,结果由函数返回,其小 Fibonacci数列F(n)的定义为:
F(0)=0, F(1)=1 ’
F(n)=F(n-1)+F(n-2)
最后调用函数writeDat(),把结果输出到文件OUT10.DAT中。
例如:当t=1000时,函数值为1597。
注意:部分源程序已给出。
请勿改动主函数main()和写函数WriteDat()的内容。
试题程序:
include
int jsValue(int t)
{
}
main ( )
{
int n;
n=1000;
printf("n=%d, f=%d\n", n, jsValue(n));
writeDat();
}
writeDat()
{
FILE *in, *out;
int n,s;
out = fopen("OUT10.DAT", "w");
s = jsValue(1000); printf("%d",s);
fprintf(out, "%d\n", s);
fclose(out);
}
正确答案:int jsValue(int t) { int f1=0f2=1fn; fn=f1+f2; while(fn=t){f1=f2;f2=fn;fn=f1+f2;} /*如果当前的Fibonacci数不大于t则计算下一个Fibonacci数*/ return fn; /*返回Fibonacci数列中大于亡的最小的一个数*/
int jsValue(int t) { int f1=0,f2=1,fn; fn=f1+f2; while(fn=t){f1=f2;f2=fn;fn=f1+f2;} /*如果当前的Fibonacci数不大于t,则计算下一个Fibonacci数*/ return fn; /*返回Fibonacci数列中大于亡的最小的一个数*/ 解析:解答本题的关键是要充分理解题意,只有理解了题意本身的数学过程,才能把数学过程转化为程序逻辑。根据已知数列,我们不难发现:Fibonacci数列中,从第三项开始,每一项都可以拆分为前两项之和。本题要求找到该数列中“大于t的最小的一个数”。这里可以借助一个while循环来依次取数列中的数,直到出现某一项的值大于t,那么这一项就是“大于t的最小的一个数”。注意:在循环体内部,我们用变量f1始终来表示第n项的前面第二项,用变量f2来始终表示第n项的前面第一项。这就实现了变量的活用与巧用。 -
第5题:
编写函数,isValue(),它的功能是求Fibonacci数列中大于t的最小的一个数,结果由函数返回,其中 Fibonacci数列F(n)的定义为:
F(0)=0,F(1)=1
F(n)=F(n-1)+F(n-2)
最后调用函数writeDat(),把结果输出到文件OUTl0.DAT中。
例如:当t=1000时,函数值为1597。
注意:部分源程序已给出。
请勿改动主函数main()和写函数WriteDat()的内容。
include <stdio.h>
int jsValue(int t)
{
}
main ( )
{
int n;
n=1000;
printf("n=%d, f=%d\n", n, jsValue(n));
writeDat ();
}
writeDat ()
{
FILE *in, *out;
int n, s;
ut = fopen ("OUT10.DAT", "w");
s = jsValue(1O00); printf("% d",s);
fprintf(out, "%d\n", s);
fclose (out);
}
正确答案:int jsValue(int t) { int f1=0f2=1fn; fn=f1+f2; while(fn=t) {f1=f2;f2=fn;fn=f1+f2;) /*如果当前的Fibonacci数不大于t 则计算下一个Fibonacci数*/ return fn; /*返回Fibonacci数列中大于t的最小的一个数*/ }
int jsValue(int t) { int f1=0,f2=1,fn; fn=f1+f2; while(fn=t) {f1=f2;f2=fn;fn=f1+f2;) /*如果当前的Fibonacci数不大于t, 则计算下一个Fibonacci数*/ return fn; /*返回Fibonacci数列中大于t的最小的一个数*/ } 解析:解答本题的关键是要充分理解题意,只有理解了题意本身的数学过程,才能把数学过程转化为程序逻辑。根据已知数列,我们不难发现:Fibonacci数列中,从第三项开始,每一项都可以拆分为前两项之和。本题要求找到该数列中“大于t的最小的一个数”。这里可以借助一个while循环来依次取数列中的数,直到出现某一项的值大于t,那么这一项就是“大于t的最小的一个数”。注意:在循环体内部,我们用变量f1始终来表示第n项的前面第二项,用变量侵来始终表示第n项的前面第一项。这就实现了变量的活用与巧用。 -
第6题:
请编写一个函数long Fibo(int n), 该函数返回n的Fibonacci数。规则如下:n等于1或者2时,Fibonacci数为1,之后每个Fibonacci数均为止前两个数之和, 即:F(n)=F(n-1)+F(n-2)
注意:清使用递归算法实现该函数。
部分源程序已存在文件test1_2.cpp中。
请勿修改主函数main和其他函数中的任何内容,仅在函数Fibo的花括号中填写若干语句。如n=8时,结果是21。
文件test1_2.cpp清单如下:
include<iostream.h>
corlsh int N=8;
long Fibo(int n);
void main()
{
long f=Fibo(N);
couk<<f<<endl;
}
long Fibo(int n)
{
}
正确答案:long Fibo(int n) { if(n==1)return 1L; else if(n==2) return 1L; else return Fibo(n-1)+Fibo(n-2); }
long Fibo(int n) { if(n==1)return 1L; else if(n==2) return 1L; else return Fibo(n-1)+Fibo(n-2); } 解析:本题考查的是考生对于递归函数的熟练掌握。递归是指在调用函数的过程中出现调用该函数自身,这里递归的结束条件是n等于1或2,即已知数列前两项为1。其调用过程如下:如果函数的参数为l或者2就把返回值1返回调用函数;否则,就使用递推公式Fibo(n)=Fibo(n-1)+Fibo(n-2),把n-1和n-2作为参数调用原函数,即这是一个递归求值的过程(递推的过程)。 -
第7题:
编写函数jsValue(int t),它的功能是:求Fibonacci数列中大于t的最小的一个数,结果由函数返回。其中Fibonacci数列F(n)的定义为: F(0)=0,F(1)=1 F(n)=F(n-1)+F(n-2) (n≥2) 最后调用函数writeDat读取l0个数据t,分别得出结果且把结果输出到文件out.dat中。 例如:当t=1000时,函数值为:1597。 注意:部分源程序存在test.c文件中。 请勿改动数据文件in.dat中的任何数据、主函数main和写函数writeDat的内容。
 正确答案:
正确答案:
【审题关键句】F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n2)。
【解题思路】
①定义表示Fibonacci数列中第F(n-2)项的变量f0,第F(n-1)项的变量n,第F(n)项的变量f2。
②当Fibonacci数列中第F(n)项的值f2小于t时,把数列当前第F(n-1)项的值n赋给f0,把数列当前第F(n)项的值f2赋给n,根据Fibonacci数列的递推关系,第n项的值等于第n-1项的值与第n-2项值的和,计算数列当前第n+1项的值f2= f0+n。依次循环,当f2的值大于t时,退出while循环,把f2的值返回。
【参考答案】

-
第8题:
以下程序的输出结果是
#include<stdio.h>
int fun(int n,int *s)
{ int f1,f2;
if(n==0||n==1)
*s=1;
else
{ fun(n-1,&f1);
fun(n-2,&f2);
*s=f1+f2;
} }
void main()
{ int x;
fun(6,&x);
printf("\n%d",x);}
A.7
B.13
C.9
D.10
正确答案:B
解析:考查函数的递归调用。n=0或n=1是递归的终止条件,然后利用已知值逐步递推求出未知值。 通过传送地址值,在被调用函数中直接改变调用函数中的变量的值。 -
第9题:
有以下程序
#include<stdio.h>
void fun(int n,int *p)
{
int f1,f2;
if(n==1||n==2) *p=1;
else
{
fun(n-1,&f1); fun(n-2,&f2);
p=f1+f2;
}
}
main()
{
int s;
fun(3,&s); printf(“%d\n”,s);
}
程序运行的结果为( )。
A.2
B.3
C.4
D.5
正确答案:A
-
第10题:
菲波那契(Fibonacci)数列定义为
f(1)=1,f(2)=1,n>2时f(n)=f(n-1)+f(n-2)
据此可以导出,n>1时,有向量的递推关系式:
(f(n+1),f(n))=f(f(n),f(n-1))A
其中A是2*2矩阵(64)。从而,f(n+1),f(n)=(f(2),f(1))*(65).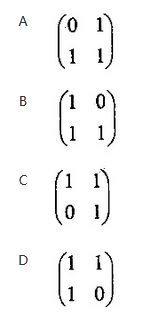 答案:D解析:本题考查数学应用的基础知识。
答案:D解析:本题考查数学应用的基础知识。
若矩阵A选取(64)中的D,则
(f(n),f(n-1))A=(f(n)+f(n-1),f(n))=(f(n+1),f(n))
由递推关系(f(n+1),f(n))=(f(n),f(n-1))A,
得到(f(n+1),f(n)):(f(n),f(n-1))A=f(n-1),f(n-2))A2=(f(n-2),f(n-3))A3=...
=(f(2),f(1)An-1=(1,1)An-1
这就给出了计算菲波那契数列的另一种算式。 -
第11题:
收集了n组数据(xi,yi), i =1, 2,…n,在一元线性回归中用SR表示回归平方和, SE表示残差平方和,由此求得F比,则当( )时在显著性水平a上认为所得到的回归方程是有意义的。
A. F>F1-a(1, n) B. F>F1-a(1, n-1)C. F>F1-a(1, n-2) D. F1-a(1, n-2)答案:C解析:由于fR =1,fE =fT-fR =n-1-1= n -2,所以在显著性水平a上,当F>F1-a(1, n-2) 时认为所得到的回归方程是有意义的。 -
第12题:
单选题若P位于第一年末,F位于第n年初,复利利率为i,则P的表达式是()AP=F(P/F,i,n)(F/P,i,1)
BP=F(P/F,I,n)
CP=F(P/F,I,n-2)
DP=F(P/F,I,n-1)(F/P,I,2)
正确答案: A解析: 暂无解析 -
第13题:
有以下程序
#include<stdi0.h>
void fun(int n,int*p)
( int f1,f2;
if(n==1|| n==2)*p=1;
else
{ fun(n-1,&f1);fun(n-2,&f2);
*p=f1+f2;
}
}
main
{ int s;
fun(3,&s);printf("%d",s);
}
程序的运行结果是( )。
A.2
B.3
C.4
D.5
正确答案:A
在函数fun中对参数n的值进行判断,如果其值等于1或2,则*p=1,否则,函数fun进行递归调用fun(n.1,&f1);fun(13.2,&f2);*p=n+f2;在主函数调用fun函数时传递给参数n的值为3,fun函数又递归用了两次自身fun(2,&n);fun(1,&f1);所以n和f2的值都为1,通过指针P的引用,变量S的值为2。 -
第14题:
编写函数jsValue(),它的功能是求Fibonacci数列中大于t的最小的一个数,结果由函数返回,其中Fibonacci数列F(n)的定义为:
F(0)=0, F(1)=1
F(n)=F(n-1)+F(n-2)
最后调用函数writeDat(),把结果输出到文件OUT10.DAT中。
例如:当t=1000时,函数值为1597。
注意:部分源程序已给出。
请勿改动主函数main()和写函数WriteDat()的内容。
试题程序:
include<stdio.h>
int jsValue(int t)
{
}
main()
{
int n;
n=1000;
printf("n=%d, f=%d\n", n,jsValue(n));
writeDat();
}
writeDat()
{
FILE *in, *out;
int n,s;
ut = fopen("OUT10.DAT", "w");
s = jsValue(1000); printf("%d",s);
fprintf(out, "%d\n", s);
fclose(out);
}
正确答案:int jsValue(int t) { int f1=0f2=1fn; fn=f1+f2; while(fn=t) {f1=f2;f2=fn;fn=f1+f2;} /*如果当前的Fibonacci数不大于t则计算下一个 Fibonacci数*/ return fn; /*返回Fibonacci数列中大于t的最小的一个数*/ }
int jsValue(int t) { int f1=0,f2=1,fn; fn=f1+f2; while(fn=t) {f1=f2;f2=fn;fn=f1+f2;} /*如果当前的Fibonacci数不大于t,则计算下一个 Fibonacci数*/ return fn; /*返回Fibonacci数列中大于t的最小的一个数*/ } 解析:解答本题的关键是要充分理解题意,只有理解了题意本身的数学过程,才能把数学过程转化为程序逻辑。根据已知数列,我们不难发现:Fibonacci数列中,从第三项开始,每一项都可以拆分为前两项之和。本题要求找到该数列中“大于t的最小的一个数”。这里可以借助一个while循环来依次取数列中的数,直到出现某一项的值大于t,那么这一项就是“大于t的最小的一个数”。注意:在循环体内部,我们用变量f1始终来表示第n项的前面第二项,用变量f2来始终表示第n项的前面第一项。这就实现了变量的活用与巧用。 -
第15题:
已知数列的递推公式如下:
f(n)=1 当n=0,1时
f(n)=f(n-1)+f(n-2) 当n>1时
则按照递推公式可以得到数列:1,1,2,3,5,8,13,21,34,55,……。现要求
从键盘输入n值,输出对应项的值。例如当输入n为8时,应该输出34。程序如下,
请补充完整。
Private Sub runll_Click()
f0=1
f1=1
num=Val(InputBox("请输入一个大于2的整数:"))
For n=2 To 【 】
f2=【 】
f0=f1
f1=f2
Next n
MsgBox f2
End Sub
正确答案:num f0+f1
num f0+f1 解析:程序首先需要接受用户输入的值,根据程序代码可以判断,使用变量num来存放用户输入的值,使用循环实现递推,根据题面“要求从键盘输入n值,输出对应项的值”,可知循环从2开始,到用户输入的值结束,也就是“Forn=2 To num”。根据题面给出的公式“当n>1时,f(n)=f(n-1)+f(n-2)”,可知第n项的值总等于它前两项(即第n-2项与第n-1项)之和,在程序For循环中,总用f2表示第n项,f0表示第n-2项,f1表示第n-1项,所以f2=f0+f1。 -
第16题:
编写函数jsvalue(),其功能是:求Fibonacci数列中大于t的最小的一个数,结果由该函数返回。其中,Fibonacci数列F(n)的定义如下。F(0)=0, F(1)=1F(n)=F(n-1)+F(n-2)最后,调用函数writeDat()读取10个数据t,分别得出结果,并把结果输出到文件out.dat中。例如:当t=1000时,函数值为1597。部分源程序已给出。请勿改动主函数main()和写函数writeDat()的内容。#include <stdio.h>int jsValue(int t){ }void writeDat(){ FILE *in, *out; int i, n, s; in = fopen("in.dat", "r"); out = fopen("out.dat", "w"); for (i=0; i<50; i++) { fscanf(in, "%d,", &n); s = jsValue(n); fprintf(out, "%d\n", s); } fclose(in); fclose(out);}main(){ int n; n = 1000; printf("t=%d,f=%d\n", n, jsValue(n)); writeDat();}
正确答案:参考试题解析
【解析及答案】
本题属于按条件查找类型的题目,考核的知识点为:求解Fibonacci数列的第n项的值;查找满足条件的Fibonacci数列的第n项的值。
本题的解题思路为:从第1项开始逐个求出Fibonacci数列的每一项的值,并且将其与给定的数据相比较,若找到第1个大于给定数据的值则将其返回。程序的流程为:调用jsvalue(n)函数处理数据,由writeDat()函数将数据写回到文件out.dat中。在jsvalue()函数中,根据题目给出的条件,Fibonacci数列中的每一项的值均为前两项之和。将Fibonacci数列的每一项的都初始化,然后通过while循环的条件进行判断:当Fn≤t,即第n项的值小于1000时,进入while循环体,计算Fn的值,每计算一个Fn的值就与t比较一次,直到fn>t,即找到大于t的最小的一个数时,循环结束。该while循环的功能就是查找比t大的Fn的值。while循环结束后,利用return语句返回Fn的值,函数结束。
int jsvalue(int t)
{ int f1=0,f2=1,fn;
fn=f1+f2;
while(fn<=t)
{f1=f2;
f2=fn;
fn=f1+f2;}
return fn;
} -
第17题:
以下程序的输出结果是()。includeint fun(int n,int *s){ int f1,f2;if(n==0||n==1)*s= 以下程序的输出结果是( )。 #include<stdio.h> int fun(int n,int *s) { int f1,f2; if(n==0||n==1) *s=1; else { fun(n-1,&f1); fun(n-2,&f2); *s=f1+f2; } } void main() { int x; fun(6,&x); printf("\n%d" ,x);}
A.7
B.13
C.9
D.10
正确答案:B
解析:n=0或n=1是递归的终止条件。然后利用已知值逐步递推求出未知值。注意:通过传送地址值,在被调用函数中直接改变调用函数中的变量的值。 -
第18题:
有以下程序:includeiht fun(iht n,int*p){int f1,f2;if(n==1||,n==2)*p=1;else{fun(n- 有以下程序: #include<stdio.h> iht fun(iht n,int*p) { int f1,f2; if(n==1||,n==2)*p=1; else { fun(n-1,&f1);fun(n-2,&f2); *p=f1+f2; } } main() { int s; fun(3,&s); printf("%d\n",s); } 程序的运行结果是______。
A.2
B.3
C.4
D.5
正确答案:A
解析: 本题考查的重点是理解递归函数。fun()为递归函数,递归结束条件时n为1或2,从而fun(3,&s)得fun(2,&s)+fun(1,&s)=1+1=2,因此选项A是正确的。 -
第19题:
请编写函数proc(),它的功能是求Fibonacci数列中小于n的最大的一个数,结果由函数返回。
Fibonacci数列F(n)的定义为
F(0)=O,F(1)=1
F(n)=F(n-1)+F(n-2)
例如,n=500时,函数值为377。
注意:部分源程序给出如下。
请勿改动main()函数和其他函数中的任何内容,仅在函数proc()的花括号中填写所编写的若干语句。
试题程序:
 正确答案:
正确答案:
【解析】由题目中所给的公式可知,Fibonacci数列的第n项为第n-1项和第n-2项的和。要求Fibonacci数列中小于n的最大的一个数。首先根据公式求出Fibonacci数列的第n项的值,当第i项大于n,则返回第i-1项的值。 -
第20题:
设n位二进制数(从00…0到11…1)中不含连续三位数字相同的数共有F(n)个,显然F(1)=2,F(2)=4。以下选项中有一个公式是正确的,通过实例验证选出的是( )。
A.F(n)=2n (n≥1) B.F(n)=n2-n+2 (n≥1) C.F(n)=F(n-1)+4n-6 (n≥2) D.F(n)=F(n-1)+F(n-2) (n≥3)
正确答案:D
-
第21题:
菲波那契(Fibonacci)数列定义为
f(1)=1,f(2)=1,n>2时f(n)=f(n-1)+f(n-2)
据此可以导出,n>1时,有向量的递推关系式:
(f(n+1),f(n))=f(f(n),f(n-1))A
其中A是2*2矩阵()。从而,f(n+1),f(n)=(f(2),f(1))*(65).A.An-1
B.An
C. An+1
D. An+2答案:A解析:本题考查数学应用的基础知识。
若矩阵A选取(64)中的D,则
(f(n),f(n-1))A=(f(n)+f(n-1),f(n))=(f(n+1),f(n))
由递推关系(f(n+1),f(n))=(f(n),f(n-1))A,
得到(f(n+1),f(n)):(f(n),f(n-1))A=f(n-1),f(n-2))A2=(f(n-2),f(n-3))A3=...
=(f(2),f(1)An-1=(1,1)An-1
这就给出了计算菲波那契数列的另一种算式。 -
第22题:
设n位二进制数(从00…0到11…1)中不含连续三位数字相同的数共有F(n)个,显然F(1)=2,F(2)=4。以下选项中有一个公式是正确的,通过实例验证选出的是( )。A.F(n)=2n (n≥1)
B.F(n)=n2-n+2 (n≥1)
C.F(n)=F(n-1)+4n-6 (n≥2)
D.F(n)=F(n-1)+F(n-2) (n≥3)答案:D解析:本题考查数学应用(排列组合)基本能力。
当n=3时,除3位全0或全1外,其他情况都是不含连续3位数字相同,因此F(n)=8-2=6。当n=4时,除0001、1000、0000、1110、0111、1111外,其他情况都不含连续3位数字相同,因此F(n)=16-6=10。
供选答案A、B、C、D中,对于n=1~4,F(n)的值如下:
因此,可以选出公式D是正确的。
当n=5时,除000**、1000*、01000、11000;111**、0111*、00111、10111外,其他情况都是不含连续3位数字相同,因此,F(n)=32-16=16。
进一步计算表明,n≥3时,n位二进制数中不含连续三位数字相同的数中,末两位数字不同的数有F(n-1)个,末两位数字相同的数有F(n-2)个。 -
第23题:
下面是用递推法计算菲波那(Fibonacci)级数第n项的函数,请填补空缺。int f(int n)int f0=0,fl=1,f,i;if(n==0)return 0;if(n==1)return 1;for(i=2;i<=n;i++){f=f0+fl;f0 f1;( );}return f;}A.f=f1
B.f1=f0
C.f=f0
D.f1=f答案:D解析:本题考查C语言编程及算法方面的基础知识。菲波那(Fibonacci)级数数列为0,1,1,2,3,5,8,13,…,即:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)当n>1时。
