采用贪心算法保证能求得最优解的问题是（ ） A.0-1背包 B.矩阵连乘 C.最长公共子序列 D.邻分（分数）背包

题目
采用贪心算法保证能求得最优解的问题是（ ）

A.0-1背包
B.矩阵连乘
C.最长公共子序列
D.邻分（分数）背包
相似考题

1.贪心算法与动态规划算法的共同点是()A.重叠子问题B.构造最优解C.贪心选择性质D.最优子结构性质

2.贪心算法的基本要素是贪心选择质和最优子结构性质。()此题为判断题(对，错)。

3.不能保证求得0-1背包问题的最优解。A．分支限界法B．贪心算法C．回溯法D．动态规划策略

4.下面是贪心算法的基本要素的是()A.重叠子问题B.构造最优解C.贪心选择性质D.定义最优解

更多“采用贪心算法保证能求得最优解的问题是（ ） ”相关问题

  • 第1题：

    如果问题有解,A*算法能保证找到问题的最优解。()

    此题为判断题(对，错)。


    参考答案：对

  • 第2题：

    贪心算法是一种______的算法。

    A．不求最优，只求满意

    B．只求最优

    C．求取全部可行解

    D．求取全部最优解


    正确答案：A
    解析：贪心算法是一种不追求最优解，只希望得到较为满意解的方法，一般可以快速得到满意的解，因为省去了为找到最优解要穷尽所有可能而必须耗费的大量时问。

  • 第3题：

    ● （65） 不能保证求得0-1 背包问题的最优解。

    （65）

    A. 分支限界法

    B. 贪心算法

    C. 回溯法

    D. 动态规划策略


    正确答案：B

  • 第4题：

    下列算法中通常以自底向下的方式求解最优解的是（）

    • A、分治法
    • B、动态规划法
    • C、贪心法
    • D、回溯法

    正确答案:B

  • 第5题：

    一般背包问题的贪心算法可以获得最优解吗？物品的选择策略是什么？


    正确答案:按照p[i]/w[i]≥p[i+1]/w[i+1]排序，选择当前利润/重量比最大的物品，可以获得最优解。

  • 第6题：

    贪心算法的基本要素是（）和最优子结构性质。


    正确答案:贪心选择性质

  • 第7题：

    一个问题可用动态规划算法或贪心算法求解的关键特征是问题的（）。

    • A、重叠子问题
    • B、最优子结构性质
    • C、贪心选择性质
    • D、定义最优解

    正确答案:B

  • 第8题：

    贪心法用于求解某目标函数在一定约束条件的最优解。它是从一个可行解（满足约束条件，但未必能使目标函数最优）出发，逐步改进解，以求得最优解的思想方法。但使用贪心法未必一定能够找到最优解。


    正确答案:正确

  • 第9题：

    单选题
    下列算法中通常以自底向下的方式求解最优解的是（）
    A

    分治法

    B

    动态规划法

    C

    贪心法

    D

    回溯法


    正确答案： D
    解析： 暂无解析

  • 第10题：

    判断题
    贪心法用于求解某目标函数在一定约束条件的最优解。它是从一个可行解（满足约束条件，但未必能使目标函数最优）出发，逐步改进解，以求得最优解的思想方法。但使用贪心法未必一定能够找到最优解。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第11题：

    单选题
    采用动态规划策略求解问题的显著特征是满足最优性原理，其含义是（）。
    A

    当前所作决策不会影响后面的决策

    B

    原问题的最优解包含其子问题的最优解

    C

    问题可以找到最优解，但利用贪心算法不能找到最优解

    D

    每次决策必须是当前看来的最优决策才可以找到最优解


    正确答案： D
    解析： 暂无解析

  • 第12题：

    单选题
    （）是贪心算法与动态规划算法的共同点。
    A

    重叠子问题

    B

    构造最优解

    C

    贪心选择性质

    D

    最优子结构性质


    正确答案： B
    解析： 暂无解析

  • 第13题：

    对于本试题的作业处理问题，用图3-25的贪心算法能否求得最高收益? (6)。(能或不能)

    用贪心算法求解任意给定问题时，是否一定能得到最优解? (7)。(能或不能)


    正确答案：
    这是一道判断贪心算法是否能求得最优解的应用分析题。对于本试题的作业处理问题，用图3-25的贪心算法策略，能求得最优解(即能求得最高收益)。但不是所有的问题都能通过贪心策略来求得最优解，一个典型的例子是0—1背包问题。例如，有3件物品，背包可容纳50磅重的东西，每件物品的详细信息如表3-14所示，问如何装包使得其价值最大? 如果按贪心策略求解该问题，优先选择单位价值最大的物品，则先选择物品R，然后选择物品S。由于此时背包容量还剩下50-10-20=20，不足以容纳物品T，故总价值为60+100=160美元。但若选择物品 S和物品T，容量总和为20+30，小于等于总容量50，得到总价值为100+120=220美元，会得到更优解。此时用贪心策略不能得到最优解。

  • 第14题：

    对于本题的作业处理问题，用图4-1的贪心算法策略，能否求得最高收益?(6)。用贪心算法求解任意给定问题时，是否一定能得到最优解?(7)。


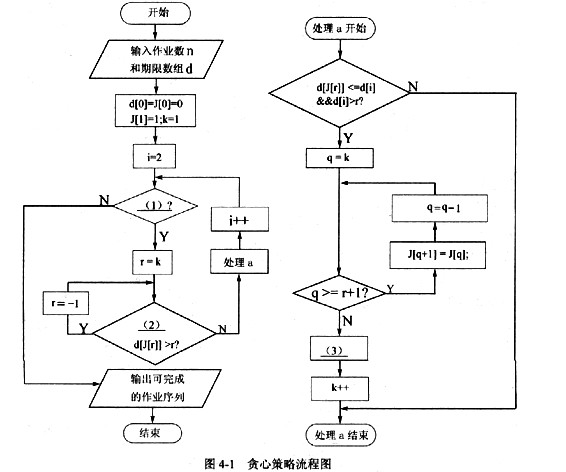    正确答案：(6)能或可以、行及其他含义相同的词语 (7)不能或不可以、不行及其他含义相同的词语
    (6)能，或可以、行及其他含义相同的词语 (7)不能，或不可以、不行及其他含义相同的词语 解析：本题考查的是算法的设计和分析技术。
    问题1考查的是贪心算法的流程图。第(1)空表示第2个作业到第n个作业的主循环，i是循环控制变量，故第(1)空填入i<=n。
    应注意到数组／中的作业J[i](1≤i≤k)是在其期限之前完成的作业，且d[J[i]]≤d[J[i+1]] (1≤id[i]。另一方面， J[D[R]]与r的关系只有两种：J[d[r]]>r，表示还可能在J[1]与J[r]之间插入作业i；J[d[r]]=r，表示不可能在J[1]～J[r]之间插入作业i。J[d[r]]问题2是本题算法的一个实例。6个作业的收益已经按降序排好序。根据流程图，将作业1，2，4和5放入数组J中，并得到总收益为220，具体过程如表4-1所示。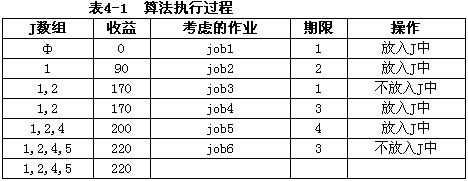

    问题3考查算法策略。对于该题，贪心策略可以求得最优解。但不是所有的问题都能通过贪心策略来求得最优解，一个典型的例子是0-1背包问题。举例如下，有三件物品，背包可容纳50磅重的东西，每件物品的详细信息如表4-2所示，问如何装包使得其价值最大?

    如果按贪心策略求解该问题，优先选择单位价值最大的物品，则先选择物品1，然后选择物品2。由于此时背包容量还剩下50-10-20=20，不足以容纳物品3，故总价值为 60+100=160美元。但若选择物品2和物品3，容量总和为20+30，小于等于总容量50，得到总价值为100+120=220，会得到更优解。此时用贪心策略不能得到最优解。

  • 第15题：

    下列算法中通常以自底向上的方式求解最优解的是（）。

    • A、备忘录法
    • B、动态规划法
    • C、贪心法
    • D、回溯法

    正确答案:B

  • 第16题：

    采用动态规划策略求解问题的显著特征是满足最优性原理，其含义是（）。

    • A、当前所作决策不会影响后面的决策
    • B、原问题的最优解包含其子问题的最优解
    • C、问题可以找到最优解，但利用贪心算法不能找到最优解
    • D、每次决策必须是当前看来的最优决策才可以找到最优解

    正确答案:B

  • 第17题：

    下面是贪心算法的基本要素的是（）

    • A、重叠子问题
    • B、构造最优解
    • C、贪心选择性质
    • D、定义最优解

    正确答案:C

  • 第18题：

    贪心算法与动态规划算法的主要区别是（）。

    • A、最优子结构
    • B、贪心选择性质
    • C、构造最优解
    • D、定义最优解

    正确答案:B

  • 第19题：

    （）是贪心算法与动态规划算法的共同点。

    • A、重叠子问题
    • B、构造最优解
    • C、贪心选择性质
    • D、最优子结构性质

    正确答案:D

  • 第20题：

    能采用贪心算法求最优解的问题，一般具有的重要性质为：（）

    • A、最优子结构性质与贪心选择性质
    • B、重叠子问题性质与贪心选择性质
    • C、最优子结构性质与重叠子问题性质
    • D、预排序与递归调用

    正确答案:A

  • 第21题：

    单选题
    一个问题可用动态规划算法或贪心算法求解的关键特征是问题的（）。
    A

    重叠子问题

    B

    最优子结构性质

    C

    贪心选择性质

    D

    定义最优解


    正确答案： C
    解析： 暂无解析

  • 第22题：

    单选题
    贪心算法与动态规划算法的主要区别是（）。
    A

    最优子结构

    B

    贪心选择性质

    C

    构造最优解

    D

    定义最优解


    正确答案： C
    解析： 暂无解析

  • 第23题：

    问答题
    一般背包问题的贪心算法可以获得最优解吗？物品的选择策略是什么？

    正确答案： 按照p[i]/w[i]≥p[i+1]/w[i+1]排序，选择当前利润/重量比最大的物品，可以获得最优解。
    解析： 暂无解析

相关内容