设机器码的长度为8位，已知[X]原=[Y]补＝1111 1111，且X和Y都是带符号的整数，则X和Y的真值分别为（ ）。A.-127,-127 B.-1,-127 C.-127,-1 D.-1,-1
题目
B.-1,-127
C.-127,-1
D.-1,-1
相似考题
更多“设机器码的长度为8位，已知[X]原=[Y]补＝1111 1111，且X和Y都是带符号的整数，则X和Y的真值分别为（ ）。”相关问题
-
第1题：
●设机器码的长度为 8，x 为带符号纯小数，y 为带符号纯整数， [X]原 ＝11111111， [Y]补＝11111111 ，则 x 的十进制真值为 （19） ，y的十进制真值为 （20） 。
（19）
A. 1/128
B. –1/128
C. –127/128
D. 127/128
（20）
A. –1
B. 127
C. –127
D. 1
正确答案：C,A
-
第2题：
设机器码的长度为8位，已知x，z为带符号纯整数，y为带符号纯小数，[X]原=[Y]补=[Z]移=11111111，求出x、y、z的十进制真值：X=(11)Y=(12)，Z=(13)。
A．127
B．-1
C．-127
D．1
正确答案：C
解析：X的原码为11111111，易得X为负数，真值为-01111111=-127。Y的补码为11111111，Y也是负数，所以Y等于Y的补码减1，即1.1111111-10=-0.0000001=-1/128。Z为定点整数，所以Z=11111111-10000000=01111111=127。 -
第3题：
已知x，z为带符号纯整数，y为带符号纯小数，而且[X]原=[Y]补=[Z]移=11111101，求出x、y、z的十进制真值：X=(98)，Y=(99)，Z=(100)。
A．-127
B．125
C．-125
D．1
正确答案：C
-
第4题：
设x=061，y=016，则z=x|y的值是( )。
A．1111
B．1.11111e+007
C．111111
D．1.1e+007
正确答案：C
解析：本题主要考查按位或运算，x=061(二进制为00110001)，y=016(二进制为00001110)，进行或运算后结果为00111111。 -
第5题：
设机器字长为8，已知X、Y分别为带符号的纯小数和纯整数，且[X]补=[Y]移=11111111，求出 X和Y的十进制真值：X=(9)，Y=(10)。
A．1/128
B．-0.0078125
C．127/128
D．-0.9921875
正确答案：B
解析：由[X]补=1111111可知[X]反=11111110以及[X]原=10000001，即X=(-0.0000001)2，(-1/128)10。 -
第6题：
设U是所有属性的集合，X、Y、Z都是U的子集，且Z=U-X-Y，下列关于多值依赖的叙述中，( )是正确的。
Ⅰ、若X→→Y，则X→Y
Ⅱ、X→Y，则X→→Y
Ⅲ、若X→→Y， 且Y′→Y， 则X→→Y
Ⅳ、若X→→Y，则X→→Z
A．只有Ⅱ
B．只有Ⅲ
C．Ⅰ和Ⅲ
D．Ⅱ和Ⅳ
正确答案：D
解析：多值依赖的定义是：设U是所有属性的集合，X、Y、Z都是U的子集，且Z=U-X-Y，若在R的任一关系r中，只要存在元组t，s，使得t[X]=s[X]，就必然存在元组w,v(w、v可以与s、t相同)，使得w[X]=v[X]=s[X]=t[X]，而w[Y]=t[Y]，w[Z]=s[Z]，v[Y]=s[Y]，v[Z]=t[Z]，则称Y多值依赖于X，记作X→→Y。函数依赖是多值依赖的特殊情况。多值依赖具有以下性质：①若X→→Y则X→→Z即具有对称性。②若X→Y则X→→Y。③多值依赖的有效性与属性值的范围有关。④若X→→Y在R(U)上成立，不一定有X→→Y'在R(U)上成立。由以上的性质①和性质②可以知道，Ⅱ和Ⅳ是正确的。由性质④知道，Ⅲ错误。函数依赖是多值依赖的特殊情况，反过来说就不一定对，因此Ⅰ也是错误的。 -
第7题：
设机器码的长度为8位，已知X、Z为带符号的纯整数，Y为带符号的纯小数，[X]原＝[Y]补＝[Z]移＝11111111，求出X、Y、Z的十进制真值为X＝(16)，Y＝(17)， Z＝(18)。
A．-1
B．127
C．-127
D．1
正确答案：C
-
第8题：
设U是所有属性的集合，X、Y、Z都是U的子集，且Z=U-X-Y。下面关于多值依赖的叙述中，哪个(些)是正确的? ( )
①若X→→Y，则X→Y
②若X→Y，则X→→Y
③若K→→Y，且Y'→Y，则X→→Y'
④若X→→Y，则X→→Z
A．只有②
B．只有③
C．①和③
D．②和④
正确答案：D
-
第9题：
已知x=4’b1001,y=4’0110,则x的4位补码为4’b1111，而y的4位的补码为（）
正确答案:4’b0110 -
第10题：
设机器码的长度为8位，已知x和y为有符号纯整数，z为有符号纯小数，［x］原=［y］移=补［z］F=11111111，求x、y、z的十进制真值为：x=（1），y=（2），z=（3）。空白（2）处应选择（）
- A、-1
- B、127
- C、-127
- D、1
正确答案:B -
第11题：
已知：带符号位二进制数X和Y的原码为[X]原=10011010B，[Y]原=11101011B，则[X+Y]补=（）。
- A、01111011B
- B、10000101
- C、11111011B
- D、溢出
正确答案:D -
第12题：
单选题设机器码的长度为8位，已知x和y为有符号纯整数，z为有符号纯小数，［x］原=［y］移=补［z］F=11111111，求x、y、z的十进制真值为：x=（1），y=（2），z=（3）。空白（1）处应选择（）A-1
B127
C-127
D1
正确答案： B解析： 暂无解析 -
第13题：
已知单字节整数[X]补=00011100，[Y]补=00110001，则X-Y的十进制真值是______。
A．-20
B．-21
C．-22
D．-25
正确答案：B
解析：[X]补=00011100，[Y]补=00110001，正数的原码等于补码，可见X，Y的真值分别为28、49，所以X-Y=28-49=-21 -
第14题：
已知单字节定点整数[X]补=00101100，[Y]补=00110101，求[X-Y]的十进制真值是______。
正确答案：-9
-9 -
第15题：
设机器码的长度为8，x为带符号纯小数，y为带符号纯整数，[X]原＝11111111， [Y]补＝11111111，则x的十进制真值为(3)，y的十进制真值为(4)。
A．1/128
B．-1/128
C．-127/128
D．127/128
正确答案：C
-
第16题：
设U是所有属性的集合，X、Y、Z都是U的子集，且Z=U-X-Y，下列关于多值依赖的叙述中，哪个(些)是正确的? Ⅰ．若X→→Y，则X→Y Ⅱ．X→Y，则X→→Y Ⅲ．若X→→Y，且
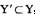,则X→→Y Ⅳ．若X→→Y，则X→→ZA．只有Ⅱ
B．只有Ⅲ
C．Ⅰ和Ⅲ
D．Ⅱ和Ⅳ
正确答案：D
解析：若X→→Y，则X→→Z，其中Z=U -X-Y，即多值依赖具有对称性；若X→Y，则X→→Y，即函数依赖可以看做多值依赖的特殊情况。若X→→Y在R(U)上成立，且[*]，我们不能断定X→→Y在R(U)上成立。 -
第17题：
设机罪码的长度为8位，已知X、Z为带符号的纯整数，Y为带符号的纯小数，[X]原+[Y]补+[Z]移=11111111，求出X、Y、Z的十进制真值为：X=(16)，Y=(17)，Z=(18)。
A．-1
B．127
C．-127
D．1
正确答案：C
解析：带符号的纯整数X用原码表示为11111111。根据原码表示法的定义，它应为一个负数，其值为-127，故X=-127。答案为C。 -
第18题：
设U是所有属性的集合，X、Y、‘Z都是U的子集，且Z=U-X-Y。下面关于多值依赖的叙述中，_______是下确的。
Ⅰ．若X→→Y，则X→Y
Ⅱ．若X→Z，则X→→Y
Ⅲ．若X→→Y，且Y'包含于Y'则X→→Y'
Ⅳ．若X→→Y，则X→→Z
A．只有Ⅱ
B．只有Ⅲ
C．Ⅰ和Ⅲ
D．Ⅱ和Ⅳ
正确答案：D
解析：多值依赖具有以下性质：1、若X→→Y，则X→→Z，所以IV是正确的。2、若X→Y，则X→→Y，所以Ⅱ是正确的，Ⅰ是错误的。3、设属性集之间的包含关系为：XY包含于W，W包含于U，那么X→→Y在R(U)上成立时，X→→Y也在R(W)上成立；反过来当X→→Y在R(W)上成立时，X→→Y在R(U)上不一定成立，即多值依赖的有效性与属性集的范围有关。4、若X→→Y，且Y，包含于Y，我们不能断言X→→Y，所以Ⅲ是错误的。 -
第19题：
设机器码的长度为8位，已知X、z为带符号的纯整数，Y为带符号的纯小数，[X]原、[Y]补和[Z]移均为11111111，X、Y、Z的十进制真值为：X=(16)，Y=(17)，Z=(18)。
A．-1
B．127
C．-127
D．1
正确答案：C
解析：(16)～(18)带符号的纯整数X用原码表示为11111111。根据原码表示法的定义，它应为一个负数，其值为-127。Y为带符号纯小数，且用补码表示，它应为一个负数，则Y=-2-7。Z为带符号纯整数，且用移码表示，转换成补码表示为[Z]补=01111111，则Z=127。 -
第20题：
设机器字长为 8，对于二进制编码 10101100，如果它是某整数x 的补码表示，则 x 的真值为（），若它是某无符号整数 y 的机器码，则 y 的真值为（请作答此空）。A.52
B.84
C.172
D.204答案：C解析：(22) 10101100化为无符号整数为：128+32+8+2=172。 -
第21题：
已知：带符号位二进制数X和Y的补码为[X]补=11001000B，[Y]补=11101111，则[X+Y]真值=（）。
- A、-55；
- B、-73；
- C、+73；
- D、溢出
正确答案:B -
第22题：
已知X和Y，试计算下列各题的[X+Y]补和[X-Y]补（设字长为8位）。 （1）X=1011，Y=0011 （2）X=1011，Y=0111 （3）X=1000，Y=1100
正确答案:（1）X补码=00001011，Y补码=00000011，[–Y]补码=11111101，[X+Y]补=00001110，[X-Y]补=00001000
（2）X补码=00001011，Y补码=00000111，[–Y]补码=11111001，[X+Y]补=00010010，[X-Y]补=00000100
（3）X补码=00001000，Y补码=00001100，[–Y]补码=11110100，[X+Y]补=00010100，[X-Y]补=11111100 -
第23题：
单选题已知：带符号位二进制数X和Y的补码为[X]补=11001000B，[Y]补=11101111，则[X+Y]真值=（）。A-55；
B-73；
C+73；
D溢出
正确答案： C解析： 暂无解析