可以用栈来检查算术表达式中的括号是否匹配。分析算术表达式时,初始栈为空,从左到右扫描字符,遇到字符“(”就将其入栈,遇到“)”就执行出栈操作。对算术表达式“(a+b*(a+b))/c)+(a+b)”,检查时,(请作答此空);对算术表达式“((a+b/(a+b)-c/a)/b”,检查时,( )。这两种情况都表明所检查的算术表达式括号不匹配。A.栈为空却要进行出栈操作 B.栈已满却要进行入栈操作 C.表达式处理已结束,栈中仍留有字符“(” D.表达式处理已结束,栈中仍留有字符“)”
题目
B.栈已满却要进行入栈操作
C.表达式处理已结束,栈中仍留有字符“(”
D.表达式处理已结束,栈中仍留有字符“)”
相似考题
参考答案和解析
更多“可以用栈来检查算术表达式中的括号是否匹配。分析算术表达式时,初始栈为空,从左到右扫描字符,遇到字符“(”就将其入栈,遇到“)”就执行出栈操作。对算术表达式“(a+b*(a+b))/c)+(a+b)”,检查时,(请作答此空);对算术表达式“((a+b/(a+b)-c/a)/b”,检查时,( )。这两种情况都表明所检查的算术表达式括号不匹配。”相关问题
-
第1题:
试题四(共 15 分)
阅读以下说明和 C 函数,将应填入 (n) 处的字句写在答题纸的对应栏内。
[说明]
计算机在处理算术表达式时,首先将其转换为后缀表达式。例如,表达式
“46+5*(120-37)”的后缀表达式形式为“46 5 120 37 - * +” 。
计算后缀表达式时,从左至右扫描后缀表达式:若遇到运算对象,则压入栈中;遇到运算符,则从栈中弹出相关运算对象进行计算,并将运算结果压入栈中,重复以上过程,直到后缀表达式扫描结束。例如,后缀表达式“46 5 120 37 - * +”的计算过程为:
a. 依次将 46、5、120、37 压入栈中;
b. 遇到“-”,取出 37、120,计算 120–37,得 83,将其压入栈中;
c. 遇到“*”,取出 83、5,计算 5*83,得 415,将其压入栈中;
d. 遇到“+”,取出 415、46,计算 46+415,得 461,将其压入栈中;
e. 表达式结束,则计算过程完成。
函数 computing(char expr[],int *result)的功能是基于栈计算后缀形式的表达式(以串形式存入字符数组 expr)的值,并通过参数 result 返回该值。函数的返回值为-1/0 分别表示表达式有/无错误。假设表达式中仅包含数字、空格和算术运算符号,其中所有项均以空格分隔,且运算符仅包含加(“+”)、减(“-”)、乘(“*”)、除(“\”)。
函数 computing 中所用栈的基本操作的函数原型说明如下:
void InitStack(STACK *s):初始化栈。
void Push(STACK *s, int e): 将一个整数压栈,栈中元素数目增 1。
void Pop(STACK *s):栈顶元素出栈,栈中元素数目减 1。
int Top(STACK s):返回非空栈的栈顶元素值,栈中元素数目不变。
int IsEmpty(STACK s):若s 是空栈,则返回1 否则返回 0。
[C 函数]
int computing(char expr[], int *result)
{
STACK s; int tnum, a,b; char *ptr;
InitStack(&s);
ptr = expr; /*字符指针指向后缀表达式串的第一个字符*/
while (*ptr!='\0') {
if (*ptr==' ') { /*当前字符是空格*/
(1) ; /*字符指针指向下一字符*/
continue;
}
else
if (isdigit(*ptr)) {
/*当前字符是数字,则将该数字开始的数字串转换为数值*/
tnum = (2) ;
while (*ptr>=’0’ && *ptr <=’9’) {
tnum = tnum * 10 + (3) ;
ptr++;
}
Push( (4) );
}
else /*当前字符是运算符或其他符号*/
if (*ptr=='+'||*ptr=='-'||*ptr =='*'||*ptr =='/'){
if (!IsEmpty(s)) {
a = Top(s); Pop(&s); /*取运算符的第二个运算数*/
if (!IsEmpty(s)) {
b = Top(s); Pop(&s); /*取运算符的第一个运算数*/
}
else return -1;
}
else return -1;
switch (*ptr) {
case '+': Push(&s,b+a); break;
case '-': Push(&s,b-a); break;
case '*': Push(&s,b*a); break;
case '/': Push(&s,b/a); break;
}
}
else
return -1;
ptr++; /*字符指针指向下一字符*/
} /* while */
if (IsEmpty(s)) return -1;
else {
(5) = Top(s); Pop(&s); /*取运算结果*/
if (!IsEmpty(s)) return -1;
return 0;
}
}
正确答案:

-
第2题:
阅读以下说明和C函数,将(1)~(5)空缺处的字句填写完整。
[说明]
计算机在处理算术表达式时,首先将其转换为后缀表达式。例如,表达式“46+5*120-37)”的后缀表达式形式为“46 5 120 37-*+”。
计算后缀表达式时,从左至右扫描后缀表达式:若遇到运算对象,则压入栈中;遇到运算符,则从栈中弹出相关运算对象进行计算,并将运算结果压入栈中。重复以上过程,直到后缀表达式扫描结束。例如,后缀表达式“46 5 120 37-*+”的计算过程如下:
a.依次将46、5、120、37压入栈中;
b.遇到“-”,取出37、120,计算120-37=83,将其压入栈中;
c.遇到“*”,取出83、5,计算5×83=415,将其压入栈中;
d.遇到“+”,取出415、46,计算46+415=461,将其压入栈中;
e.表达式结束,则计算过程完成。
函数computing(char expr[],int*result)的功能是基于栈计算后缀形式的表达式(以串形式存入字符数组 expr)的值,并通过参数result返回该值。函数的返回值为-1/0,分别表示表达式有/无错误。假设表达式中仅包含数字、空格和算术运算符号,其中所有项均以空格分隔,且运算符仅包含加(“+”)、减(“-”)、乘(“*”)、除(“\”)。
函数computing中所用栈的基本操作的函数原型说明如下。
● void InitStack(STACK*s):初始化栈。
● void Push(STACK*s,int e):将一个整数压栈,栈中元素数目增1。
● void Pop(STACK*s):栈顶元素出栈,栈中元素数目减1。
● int Top(STACK s):返回非空栈的栈顶元素值,栈中元素数目不变。
● int IsEmpty(STACKs):若s是空栈,则返回1;否则返回0。
[C函数]
 正确答案:是一道考查栈结构在后缀表达式求值过程中应用的分析题。利用栈计算后缀表达式时从左至右扫描后缀表达式:若遇到运算对象则压入栈中;遇到运算符则从栈中弹出对应数目的运算对象进行计算并将运算结果压入栈中。重复以上过程直到后缀表达式扫描结束最后栈顶就是表达式的计算结果。 根据题干中的说明由于后缀表达式以字符串方式存储且以空格分隔符号(数值、算符)因此遇到空格字符时指向表达式中字符的指针ptr应增加1指向后续字符因此(1)空缺处应填入“ptr++”或其等价形式。下面以字符串“375”为例说明将一个数字串转换为数值的过程。 数值375=((0×10+3)×10+7)×10+5 (1)取得数字字符“3”(ASCII码值为51字符0的ASCII码值为48)。
正确答案:是一道考查栈结构在后缀表达式求值过程中应用的分析题。利用栈计算后缀表达式时从左至右扫描后缀表达式:若遇到运算对象则压入栈中;遇到运算符则从栈中弹出对应数目的运算对象进行计算并将运算结果压入栈中。重复以上过程直到后缀表达式扫描结束最后栈顶就是表达式的计算结果。 根据题干中的说明由于后缀表达式以字符串方式存储且以空格分隔符号(数值、算符)因此遇到空格字符时指向表达式中字符的指针ptr应增加1指向后续字符因此(1)空缺处应填入“ptr++”或其等价形式。下面以字符串“375”为例说明将一个数字串转换为数值的过程。 数值375=((0×10+3)×10+7)×10+5 (1)取得数字字符“3”(ASCII码值为51字符0的ASCII码值为48)。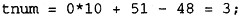 (2)取得数字字符“7” (ASCII码值为55)。
(2)取得数字字符“7” (ASCII码值为55)。
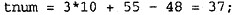 (3)取得数字字符“5” (ASCII码值为53)。
(3)取得数字字符“5” (ASCII码值为53)。
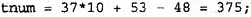 以下程序代码用于将一个数字字符串转换为对应的整数存入tnum显然tnum的初始值应为0。
以下程序代码用于将一个数字字符串转换为对应的整数存入tnum显然tnum的初始值应为0。
 因此(2)空缺处应填入“0”。对于(3)空缺所在表达式的功能是:将数字字符转换为数值因此 (3)空缺处填入“*ptr-48”。
(4)空缺处用于将转换所得的数值tnum压入栈顶根据题目中Push的原型“void Push(STACK*sint e)”调用时第一个实际参数是STACK类型变量的地址第二个实际参数是一个整数因此(4)空缺处填入“&stnum”。
由于函数computing(char expr[]int*result)通过参数result返回该表达式的值因此需要将存在栈顶的运算结果赋值给result指向的整型变量即(5)空缺处填入“*result”。
本试题目还考查了参数传递知识读者可通过上机实践加强基本概念的理解以及C程序设计能力的培养。
因此(2)空缺处应填入“0”。对于(3)空缺所在表达式的功能是:将数字字符转换为数值因此 (3)空缺处填入“*ptr-48”。
(4)空缺处用于将转换所得的数值tnum压入栈顶根据题目中Push的原型“void Push(STACK*sint e)”调用时第一个实际参数是STACK类型变量的地址第二个实际参数是一个整数因此(4)空缺处填入“&stnum”。
由于函数computing(char expr[]int*result)通过参数result返回该表达式的值因此需要将存在栈顶的运算结果赋值给result指向的整型变量即(5)空缺处填入“*result”。
本试题目还考查了参数传递知识读者可通过上机实践加强基本概念的理解以及C程序设计能力的培养。
是一道考查栈结构在后缀表达式求值过程中应用的分析题。利用栈计算后缀表达式时,从左至右扫描后缀表达式:若遇到运算对象,则压入栈中;遇到运算符,则从栈中弹出对应数目的运算对象进行计算,并将运算结果压入栈中。重复以上过程,直到后缀表达式扫描结束,最后栈顶就是表达式的计算结果。 根据题干中的说明,由于后缀表达式以字符串方式存储且以空格分隔符号(数值、算符),因此遇到空格字符时,指向表达式中字符的指针ptr应增加1指向后续字符,因此,(1)空缺处应填入“ptr++”或其等价形式。下面以字符串“375”为例说明将一个数字串转换为数值的过程。 数值375=((0×10+3)×10+7)×10+5 (1)取得数字字符“3”(ASCII码值为51,字符0的ASCII码值为48)。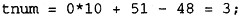 (2)取得数字字符“7” (ASCII码值为55)。
(2)取得数字字符“7” (ASCII码值为55)。
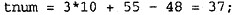 (3)取得数字字符“5” (ASCII码值为53)。
(3)取得数字字符“5” (ASCII码值为53)。
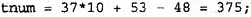 以下程序代码用于将一个数字字符串转换为对应的整数存入tnum,显然,tnum的初始值应为0。
以下程序代码用于将一个数字字符串转换为对应的整数存入tnum,显然,tnum的初始值应为0。
 因此,(2)空缺处应填入“0”。对于(3)空缺所在表达式的功能是:将数字字符转换为数值,因此 (3)空缺处填入“*ptr-48”。
(4)空缺处用于将转换所得的数值tnum压入栈顶,根据题目中Push的原型“void Push(STACK*s,int e)”,调用时第一个实际参数是STACK类型变量的地址,第二个实际参数是一个整数,因此,(4)空缺处填入“&s,tnum”。
由于函数computing(char expr[],int*result)通过参数result返回该表达式的值,因此需要将存在栈顶的运算结果赋值给result指向的整型变量,即(5)空缺处填入“*result”。
本试题目还考查了参数传递知识,读者可通过上机实践加强基本概念的理解,以及C程序设计能力的培养。
因此,(2)空缺处应填入“0”。对于(3)空缺所在表达式的功能是:将数字字符转换为数值,因此 (3)空缺处填入“*ptr-48”。
(4)空缺处用于将转换所得的数值tnum压入栈顶,根据题目中Push的原型“void Push(STACK*s,int e)”,调用时第一个实际参数是STACK类型变量的地址,第二个实际参数是一个整数,因此,(4)空缺处填入“&s,tnum”。
由于函数computing(char expr[],int*result)通过参数result返回该表达式的值,因此需要将存在栈顶的运算结果赋值给result指向的整型变量,即(5)空缺处填入“*result”。
本试题目还考查了参数传递知识,读者可通过上机实践加强基本概念的理解,以及C程序设计能力的培养。
-
第3题:
请从下面的选项中选择相应的判断逻辑填补【算法2-1】中的“判断条件1”至“判断条件3”。注意,若“判断条件2”的逻辑判断结果为假,就无需对“判断条件3”进行判断。
(a)字符是括号
(b)字符是左括号
(c)字符是右括号
(d)栈空
(e)栈不空
(f)栈顶元素表示的是与当前字符匹配的左括号
(R)栈顶元素表示的是与当前字符匹配的右括号
正确答案:判断条件1:b 判断条件2:e 判断条件3:f
判断条件1:b 判断条件2:e 判断条件3:f 解析:因为后面有"pop();row-pop();col-pop();”,所以空(5)应填col,(6)应填row。又因为判断条件1为真时需要人栈,所以判断条件1应是判断字符是不是左括号,是就人栈,所以判断条件选 b。判断条件2和3是相关联的,当2和3都为真时,要进行出栈操作,因此要判断栈是否为空。由此可以得到待判断条件2和3中,有一个必定是用来判断栈是否为空的。可以用栈顶元素来确定当前括号是否和栈中压人括号是同一类型的。前提是左括号类型已经人栈了,且在栈底,如果(7)压入的是k,即吻合。所以(7)应填k,这样判断括号是否匹配的条件就可以确定了,如果当前ch是右括号且当前栈顶的左括号类型与ch匹配,则匹配成功。应把“栈不空”作为判断条件2,“栈顶元素表示的是与当前字符匹配的左括号”作为判断条件3。这样判断条件2填e,判断条件3填f。 -
第4题:
算术表达式采用后缀式表示时不需要使用括号,使用(请作答此空)就可以方便地进行求值。a-b* (c + d)的后缀式为 ( ) 。A.队列
B.数组
C.栈
D.广义表答案:C解析:计算机在处理算术表达式时,首先将其转换为后缀表达式。例如,表达式“46+5*(120-37)”的后缀表达式形式为 “46512037-*+”。计算后缀表达式时,从左至右扫描后缀表达式:若遇到运算对象,则压入栈中,若遇到运算符,则从栈中弹出相关运算对象进行计算,并将运算结果压入栈中,重复以上过程,直到后缀表达式扫描结束。表达式“a-b*(b+d)”的后缀表达式形式为“abcd + * -。 -
第5题:
阅读以下说明和C函数,将应填入 (n) 处的字句写在答题纸的对应栏内。4、【说明】 计算机在处理算术表达式时,首先将其转换为后缀表达式。例如,表达式“46+5*(120-37)”的后缀表达式形式为“46 512037-*+”。 计算后缀表达式时,从左至右扫描后缀表达式:若遇到运算对象,则压入栈中;遇,到运算符,则从栈中弹出相关运算对象进行计算,并将运算结果压入栈中。重复以上过程,直到后缀表达式扫描结束。例如,后缀表达式“46 5120 37-*+”的计算过程如下。 a.依次将46、5、120、37压入栈中; b.遇到“-”,取出37、120,计算120-37=83,将其压入栈中: c.遇到“*”,取出83、5,计算5×83=415,将其压入栈中; d.遇到“+”,取出415、46,计算46+415=461,将其压入栈中; e.表达式结束,则计算过程完成。 函数computing(char expr[],int *result)的功能是基于栈计算后缀形式的表达式(以串形式存入字符数组expr)的值,并通过参数result返回该值。函数的返回值为-1/0,分别表示表达式有/无错误。假设表达式中仅包含数字、空格和算术运算符号,其中所有项均以空格分隔,且运算符仅包含加(“+”)、减(“-”)、乘(“*”)、除(“\”)。 函数computing中所用栈的基本操作的函数原型说明如下。 · void InitStack(STACK *s):初始化栈。 · void Push(STACK,s,int e):将一个整数压栈,栈中元素数目增1。 · void Pop(STACK *s):栈顶元素出栈,栈中元素数目减1。 · int Top(STACK s):返回非空栈的栈顶元素值,栈中元素数目不变。 · int IsEmpty(STACKs):若s是空栈,则返回1;否则返回0。【C函数】 int computing (char expr[],int *result) { STACK s; int tnum,a,b; char *ptr; InitStack(&s); ptr=expr;pstr /*字符指针指向后缀表达式串的第一个字符*/ while(*ptr!='\0') { if(*ptr==' ') { /*当前字符是空格*/ (1) ; /*字符指针指向下一字符*/ continue; } else if(isdigit (*ptr)) { /*当前字符是数字,则将该数字开始的数字串转换为数值*/ tnum= (2) ; while (*ptr>='0' && *ptr <='9') { tnum=tnum * 10 + (3) ; ptr++; } Push( (4) ); } else /*当前字符是运算符或其他符号*/ if (*ptr=='+'||*ptr=='-'||*ptr=='*'||*ptr=='/'){ if(!IsEmpty(s)) { a=Top(s);Pop(&s); /*取运算符的第二个运算数*/ if(!IsEmpty(s)) { b=Top(s);Pop(&s);/*取运算符的第一个运算数*/ } else return -1; } else return -1; switch (*ptr) { case '+': Push(&s,b+a); break; case '-':Push(&s,b-a); break; case '*':Push(&s,b*a); break; case '/':Push(&s,b/a); break; } } else return -1; ptr++; /*字符指针指向下一字符*/ }/*while*/ if(IsEmpty(s)) return -1; else{ (5) =Top(s); Pop(&s); /*取运算结果*/ if(!IsEmpty(s)) return -1; return 0; } }答案:解析:(1)ptr++,或++ptr,或ptr=ptr+1,或其等价表示 (2)0,或tnum=0 (3)*ptr-'0',或*ptr-48,或其等价表示 (4)&s,tnum (5)*result
【解析】
本题考查栈结构在后缀表达式求值过程中的应用。 利用栈计算后缀表达式时,从左至右扫描后缀表达式:若遇到运算对象,则压入栈中;遇到运算符,则从栈中弹出对应数目的运算对象进行计算,并将运算结果压入栈中。重复以上过程,直到后缀表达式扫描结束,最后栈顶就是表达式的计算结果。 根据题目的说明,由于后缀表达式以字符串方式存储且以空格分隔符号(数值、算符),因此遇到空格字符时,指向表达式中字符的指针ptr应增加1指向后续字符,因此,空(1)处应填入“ptr++”或其等价形式。 下面以字符串“375”为例说明将一个数字串转换为数值的过程。 数值375=((0×10+3)×10+7)×10+5 (1)取得数字字符“3”(ASCII码值为51,字符0的ASCII码值为48)。 mum=0*10+51-48=3; (2)取得数字字符“7” (ASCII码值为55)。 tnum=3*10+55-48=37; (3)取得数字字符“5” (ASCII码值为53)。 tnum=37*10+53-48=375; 以下代码用于将一个数字字符串转换为对应的整数存入tnum,显然,tnum的初始值应为0。 tnum= (2) ; while (*ptr>='0' && *ptr <='9') { tnum=tnum*10+ (3) ; ptr++; } 因此,空(2)处应填入“0”,空(3)所在表达式将数字字符转换为数值,即空(3)处填入“*ptr-48”。 空(4)处用于将转换所得的数值tnum压入栈顶,根据题目中Push的原型“void Push(STACK *s,int e)”,调用时第一个实际参数是STACK类型变量的地址,第二个实际参数是一个整数,因此,空(4)处填入“&s,tnum”。 由于函数computing(ckar expr[],int *result)通过参数result返回该表达式的值,因此需要将存在栈顶的运算结果赋值给result指向的整型变量,即空(5)处填入“*result”。 该题目还考查了参数传递知识,因此考生应通过上机实践加强基本概念的理解和程序设计能力的培养。 -
第6题:
算术表达式采用后缀式表示时不需要使用括号,使用(请作答此空)就可以方便地进行求值。a-b(c+d)(其中,-、+、*表示二元算术运算减、加、乘)的后缀式为( ),与该表达式等价的语法树为( )。A.队列
B.数组
C.栈
D.广义表答案:C解析: -
第7题:
算术表达式a+b*(c+d/e)可转换为后缀表达式()。
- A、abcde*/++
- B、abcde/+*+
- C、abcde*+/+
- D、abcde/*++
正确答案:B -
第8题:
算术表达式a+b/(c+d)×f的逆波兰式是()。
正确答案:abcd+/f×+ -
第9题:
使用()形式时,即使表达式中有Shell的特殊字符时,也不必用双引号将其括起来。
- A、test表达式
- B、[表达式]
- C、let算术表达式
- D、((算术表达式))
正确答案:D -
第10题:
填空题算术表达式a+b/(c+d)×f的逆波兰式是()。正确答案: abcd+/f×+解析: 暂无解析 -
第11题:
单选题使用()形式时可以返回算术表达式的确切值。Atest表达式
Blet算术表达式
C((算术表达式))
D$((算术表达式))
正确答案: C解析: 暂无解析 -
第12题:
单选题算术表达式采用逆波兰式表示时不用括号,可以利用(1)进行求值。与逆波兰式ab-cd+*对应的中缀表达式是(2)。空白(1)处应选择()A数组
B栈
C队列
D散列表
正确答案: B解析: 逆波兰式表示方式把运算符写在运算对象的后面,不需要使用括号。由于逆波兰式表示中的各个运算是按顺序执行的,因此,它的计值很容易实现。为此,仅需从左到右依次扫视表达式中的各个符号,每遇到一个运算对象,就把它压入栈顶暂存起来;每遇到一个二元(或一元)运算符时,就取出栈顶的两个(或一个)运算对象进行相应的运算,并用运算结果去替换栈顶的这两(或一)个运算对象,然后再继续扫视余留的符号,如此等等,直到扫视完整个表达式为止。当上述过程结束时,整个表达式的值将留于栈顶。a-b+c*d对应的逆波兰式为ab-cd*+。(a-b)*c+d对应的逆波兰式为ab-c*d+。(a-b)*(c+d)对应的逆波兰式为ab-cd+*。a-b*c+d对应的逆波兰式为abc*-d+。 -
第13题:
可以用栈来检查算术表达式中的括号是否匹配。分析算术表达式时,初始栈为空,从左到右扫描字符,遇到字符“(”就将其入栈,遇到“)”就执行出栈操作。对算术表达式“(a+b*(a+b))/c)+(a+b)”,检查时,(33);对算术表达式“((a+b/(a+b)-c/a)/b”,检查时,(34)。这两种情况都表明所检查的算术表达式括号不匹配。
A.栈为空却要进行出栈操作
B.栈已满却要进行入栈操作
C.表达式处理已结束,栈中仍留有字符“(”
D.表达式处理已结束,栈中仍留有字符“)”
正确答案:A
解析:对算术表达式(a+b*(a+b))/c)+(a+b)进行括号检查时,栈操作的顺序为:
入栈,入栈,出栈,出栈,出栈,……
当需要进行第三次出栈操作时,发现栈已空,已不可能完成出栈操作。
对算术表达式((a+b/(a+b)-c/a)/b进行括号检查时,栈操作的顺序为:
入栈,入栈,入栈,出栈,出栈
第1次出栈操作取出的是第3次刚入栈的“(”,第2次出栈操作取出的是第2次入栈的“(”。直到表达式检查结束,第1次入栈的“(”仍没有取出,因此,表达式中的括号并不匹配。
本例是栈的重要应用之例。编译程序中常用栈来检查语句(或程序)中的括号是否匹配。
在日常生活中,当人们进入一个复杂的大院时,需要多次进门,多次出门。每次出门,总是退出最近进门的院。在同一位置堆积货物时,总是先取最近刚放上的货。所以,栈的应用也是比较常见的。可以用这种日常生活中的例子来形象地理解栈的操作。 -
第14题:
可利用一个栈来检查表达式中的括号是否匹配,其方法是:初始时设置栈为空,然后从左到右扫描表达式,遇到左括号“(”就将其入栈,遇到右括号“)”就执行出栈操作,忽略其他符号。对于算术表达式“a*(b+c))d”,由于(),因此可判断出该表达式中的括号不匹配。A、需要进行出栈操作但栈已空
B、需要进行入栈操作但栈已满
C、表达式处理已结束,但栈中仍留有字符“(”
D、表达式处理已结束,但栈中仍留有字符“)”
正确答案:A
-
第15题:
设计算法判断一个算术表达式的圆括号是否正确配对。(提示:对表达式进行扫描,凡遇到'('就进栈,遇')'就退掉栈顶的'(',表达式被扫描完毕,栈应为空。
正确答案:
int PairBracket( char *SR)
{//检查表达式ST中括号是否配对
int i;
SeqStack S; //定义一个栈
InitStack (&s);
for (i=0; i
{ if ( S[i]=='(' ) Push(&S, SR[i]); //遇'('时进栈
if ( S[i]==')' ) //遇')'
if (!StackEmpty(S))//栈不为空时,将栈顶元素出栈
Pop(&s);
else return 0;//不匹配,返回0
}
if EmptyStack(&s) return 1;// 匹配,返回1
else return 0;//不匹配,返回0
}
-
第16题:
可利用一个栈来检查表达式中的括号是否匹配,其方法是:初始时设置栈为空,然后从左到右扫描表达式,遇到左括号“(”就将其入栈,遇到右括号“)”就执行出栈操作,忽略其他符号。在检查表达式“a*(b+c))-d”时,由于( ),因此可判断出该表达式中的括号不匹配。A.需要进行出栈操作但栈已空
B.需要进行入栈操作但栈已满
C.表达式处理已结束,但栈中仍留有字符“(”
D.表达式处理已结束,但栈中仍留有字符")”答案:A解析:第二个右括号要执行出栈操作,但没有对应的左括号可执行出栈。 -
第17题:
算术表达式采用后缀式表示时不需要使用括号,使用( )就可以方便地进行求值。a-b(c+d)(其中,-、+、*表示二元算术运算减、加、乘)的后缀式为( ),与该表达式等价的语法树为(请作答此空)。
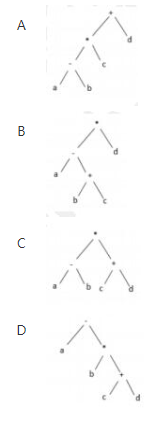 答案:D解析:
答案:D解析: -
第18题:
可利用一个栈来检查表达式中的括号是否匹配,其方法是:初始时设置栈为空, 然后从左到右扫描表达式,遇到左括号“(”就将其入栈,遇到右括号“)”就执行出栈操作,忽略其他符号。对于算术表达式“a*(b+c))d”,由于( ),因此可判断出该表达式中的括号不匹配。A. 需要进行出栈操作但栈已空
B. 需要进行入栈操作但栈已满
C. 表达式处理已结束,但栈中仍留有字符“(”
D. 表达式处理已结束,但栈中仍留有字符“)”答案:A解析:左括号入站,右括号出栈,, 该题中括号为: ( ) ) ,所以当执行第2个右括号时,第一个左括号已经出栈了,栈为空栈 -
第19题:
算术表达式采用逆波兰式表示时不用括号,可以利用(1)进行求值。与逆波兰式ab-cd+*对应的中缀表达式是(2)。空白(1)处应选择()
- A、数组
- B、栈
- C、队列
- D、散列表
正确答案:B -
第20题:
使用()形式时可以返回算术表达式的确切值。
- A、test表达式
- B、let算术表达式
- C、((算术表达式))
- D、$((算术表达式))
正确答案:D -
第21题:
单选题算术表达式a+b*(c+d/e)可转换为后缀表达式()。Aabcde*/++
Babcde/+*+
Cabcde*+/+
Dabcde/*++
正确答案: A解析: 算术表达式a+b*(c+d/e)可转换为后缀表达式abcde/+*+。 -
第22题:
单选题算术表达式a+b*(c+d/e)转为后缀表达式后为()。Aab+cde/*
Babcde/+*+
Cabcde/*++
Dabcde*/++
正确答案: C解析: -
第23题:
单选题使用()形式时,即使表达式中有Shell的特殊字符时,也不必用双引号将其括起来。Atest表达式
B[表达式]
Clet算术表达式
D((算术表达式))
正确答案: C解析: 暂无解析
