已知某工程的网络计划中相关资料如下表所示。问题：1．根据上表绘制网络计划图。2．计算总工期，以及网络图中各工作的六个时间参数(ES、EF、LS、LF、TF、FF)。3．写出关键线路（工作表示或节点表示）。

题目
已知某工程的网络计划中相关资料如下表所示。



问题：1．根据上表绘制网络计划图。2．计算总工期，以及网络图中各工作的六个时间参数(ES、EF、LS、LF、TF、FF)。3．写出关键线路（工作表示或节点表示）。

相似考题

1.已知某施工项目的计划数据资料如下表所示，则第3周的施工成本计划值是(　　)万元。A.30B.90C.60D.75

2.已知某企业可比产品成本计划降低额1800元，计划降低率3.75%。其他有关资料见下表：

3.某工程有10项工作，其相互的依赖关系如下表所示，则双代号网络计划绘制正确的是（50），其关键路径时间为（51）天。

4.绘制下列工作的网络计划:已知网络图的资料如下表表示,试用节点位置法绘出(1)双代号网(2)单代号网络图

更多“已知某工程的网络计划中相关资料如下表所示。 ”相关问题

  • 第1题：

    试题（50）、（51）

    某工程有10项工作，其相互的依赖关系如下表所示，则双代号网络计划绘制正确的是（50），其关键路径时间为（51）天。


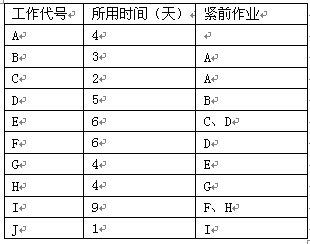
    正确答案：A,A
    试题（50）、（51）分析这是一个根据工作先后依赖关系绘制双代号网络图进而计算关键路径的计算题。首先需要弄明白各工作之间的依赖关系，同时需要注意虚工作的影响。根据题干要求，此处显然E工作的紧前工作C、D以及I工作的紧前工作F、H需要用到虚工作连接。只要看到这点，则可以使用排除法，快速找到答案，得到网络图，自然可以计算出系统的关键路径是：A、B、D、E、G、H、I、J，时间为36天。参考答案（50）A、（51）A

  • 第2题：

    某工程网络计划工作逻辑关系如下表所示，则工作A的紧后工作有（　）。

    A、工作B
    B、工作C
    C、工作D
    D、工作E
    E、工作G

    答案：A,B,C,E
    解析：
    2020版教材P137
    本题考查的是双代号网络计划。A的紧后工作就是A工作作为其紧前工作的工作。@##

  • 第3题：

    已知某投资A项目的有关资料如下表所示：

    要求：计算该项目的内含报酬率。


    答案：
    解析：
    净现值＝11 800×（P/S，i，1）＋13 240×（P/S，i，2）－20 000=0
    采用逐步测试法：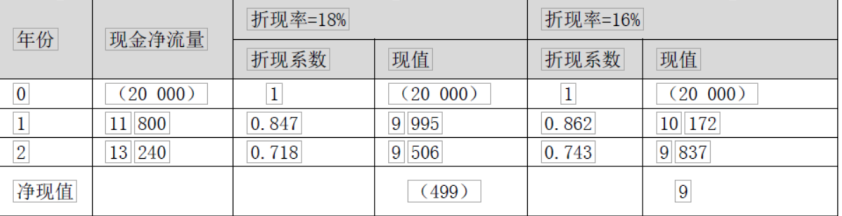

    经过以上试算，可以看出该方案的内含报酬率在16%—18%之间。采用内插法确定：

    （IRR-16%）/(0-9)=(18%-16%)/(-499-9) 解得：IRR＝16.04%

  • 第4题：

    某工程双代号网络计划如下图所示，已知计划工期等于计算工期。



    上述网络计划中，A工作的总时差TF1－2为（　）天。
    A、9
    B、5
    C、2
    D、1


    答案：A
    解析：
    本题考查的是工程网络计划的类型和应用。总时差是指在不影响整个任务按期完成的前提下，工作ｉ－ｊ必须完成的最迟时刻。本题关键工作有CGL。①－④－⑥－⑦和①－②－⑤－⑦是平行线路，所以A工作的总时差TF1－2＝15－（1＋2＋3）＝9。参见教材P135。

  • 第5题：

    某工程网络计划工作逻辑关系如下表所示，则工作 A 的紧后工作有（ ）

    A.工作 B
    B.工作 C
    C.工作 D
    D.工作 G
    E.工作 E

    答案：A,B,C,D
    解析：
    紧排在本工作之前的工作称为紧前工作。紧排在本工作之后的工作称为紧后工作。与之平行进行的工作称为平行工作。

  • 第6题：



    已知某分部工程由A、B、C、D、E五项工作组成，其网络计划如下图所示，要求该分部工程必须在20天内完成。为了保证工期，需要进行赶工，相关的数据资料如下表所示。



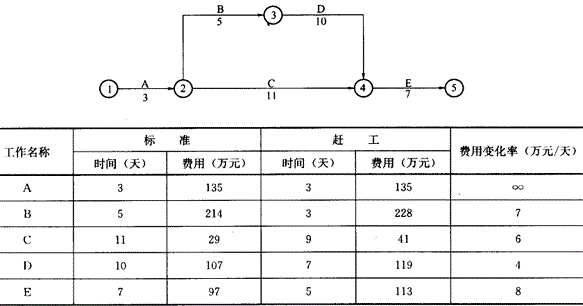
    问题：


    1.计算在标准工作情况下，该网络计划的各参数以及计划工期，并确定关键线路。


    2.试确定在规定工期20天内完成该分部工程且增加的费用最少的网络优化方案。




    答案：
    解析：

    1.计算该分部工程的各工作的时间参数，见下图。



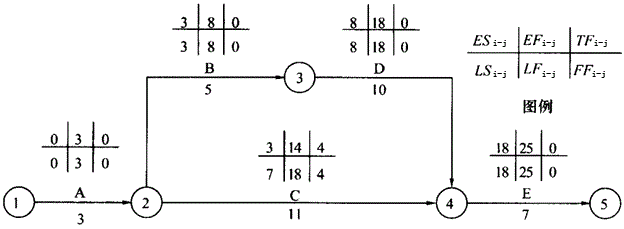
    计划工期T=25天关键线路为：A→B→D→E


    2.在规定工期20天完工，应进行赶工，赶工对象是关键线路上的关键工作，且应从增加费用最少的关键工作开始。


    (1)第一次压缩：在关键线路A→B→D→E中，D工作压缩费用变化率为4万元/天，最少，故压缩D工作，可压缩3天，压缩后的网络计划如图所示。



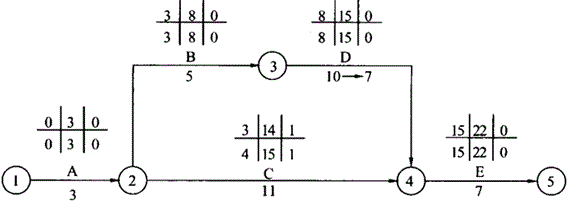
    压缩后，关键线路为：A→B→D→E。相应增加的费用为4×3=12万元，总费用为594万元，工期T1=22天。


    (2)第二次压缩：在关键线路A→B→D→E中，D工作已经压缩，不能再压缩了，B工作压缩费用变化率为7万元/天，最少，故压缩B工作，最多可压缩2天，压缩后的网络计划如图所示。



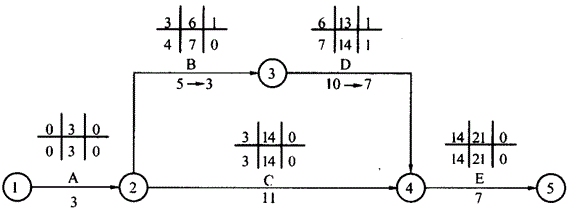
    按此方案压缩，从图中的计算可以得出，关键线路为A→C→E;工期T2=21天，相应增加的费用为7×2=14万元，总费用为608万元。此方案虽然可行，但实际上造成在节点④需要等工的情况，且造成相应的费用浪费，故不可取。因此，只压缩B工作1天，压缩后的网络计划如图所示。



    压缩后，关键线路为：A→B→D→E和A→C→E。相应增加的费用为7×1=7万元，总费用为601万元，工期T2=21天。


    (3)第三次压缩：经过前两次压缩后，两条工作线路均为关键线路，可以进行压缩的工作有B、C和E三项，可选方案有两个：其一，同时压缩工作B、C各1天;其二，压缩工作E1天。虽然B、C的费用变化率比E小，但需要同时压缩B、C工作才能满足规定的工期要求，这样压缩两项工作增加的费用必然比只压缩一项工作增加的费用多，因此，选择压缩E工作，压缩1天，压缩后的网络计划如图所示。



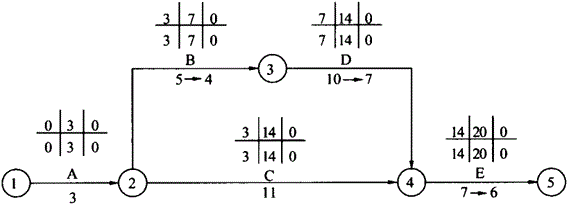
    压缩后，关键线路为：A→B→D→E和A→C→E。相应增加的费用为8×1=8万元，总费用为608万元，工期T3=20天。总之，经过几次压缩后，总工期控制在20天，相应增加的费用最少，达成目标要求。




  • 第7题：

    根据以上资料，回答以下问题：某工程项目的进度计划如下面双代号网络计划所示(时间单位：天)。

    在该网络计划中，工作F的总时差为（　　）天。

    A.2
    B.3
    C.4
    D.5

    答案：C
    解析：
    F的总时差=I的开始时间-F的最早完成时间，Ⅰ的最早开始时间=总工期-I的持续时间=19-6=13，F的最早完成时间=4+5=9，所以F的总时差=13-9=4（天）。

  • 第8题：

    已知某分部工程的进度计划如图3所示单代号网络计划。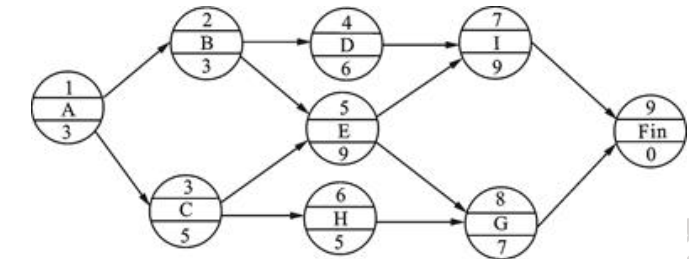

    根据以上资料，回答下列问题：
    该分部工程进度计划中的关键工作为（）。

    A.工作A、C
    B.工作B、D
    C.工作G、H
    D.工作E、I

    答案：A,D
    解析：
    在单代号网络计划中，工作总时差最小的工作是关键工作。从起点节点开始到终点节点均为关键工作，且所有工作之间的时间间隔均为零的线路为关键线路。本案例中，计算得到相邻两项工作之间的时间间隔分别为：

  • 第9题：

    共用题干
    某工程项目的进度计划如下列单代号网络计划所示，时间单位为周。

    根据以上资料，回答下列问题：

    该单代号网络计划中的关键工作为()。
    A:工作A、C
    B:工作B、D
    C:工作E、I
    D:工作H、G

    答案：A,C
    解析：
    此题考查采用网络计划编制该项目进度计划的优点。各工作之间的逻辑关系明确，能通过参数计算找出关键工作，便于对进度计划进行动态控制。
    此题考查单代号网络计划。3+5+9+9=26（周）。
    此题考查采用网络计划编制该项目进度计划的优点。各工作之间的逻辑关系明确，能通过参数计算找出关键工作，便于对进度计划进行动态控制。
    此题考查双代号网络计划。

  • 第10题：

    某施工单位编制的某工程网络进度计划图，如下图所示。该网络进度计划原始方案各工作的持续时间和估计费用，见下表。
    【问题】3.若该网络进度计划各工作的可压缩时间及压缩单位时间增加的费用，见下表。确定该网络进度计划的最低综合费用和相应的关键路线，并计算调整优化后的总工期（要求写出调整优化过程）。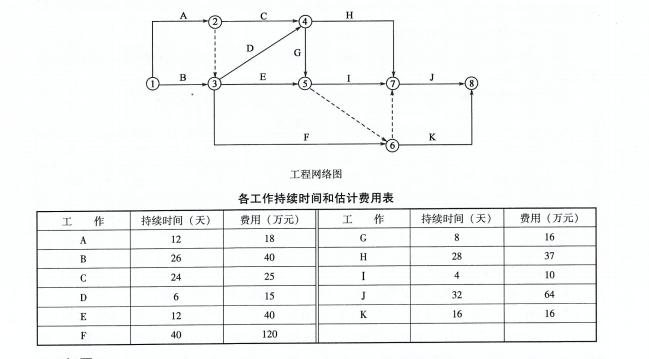


    答案：
    解析：
    3.第一次调整优化：在关键线路上取压缩单位时间增加费用最低的F工作为对象压缩2天。增加费用：2天×2万元/天=4万元。第二次调整优化：工作A、C、H、J与B、F、J同时成为关键工作，选择H工作和F工作为调整对象，各压缩2天。增加费用：2天x（l.5+2）万元/天=7万元。第三次调整优化：工作A、C、H、J与B、F、J仍为关键工作，选择A工作和F工作为调整对象，各压缩1天。增加费用：1天×（2+2）万元/天=4万元。优化后的关键线路为：①-②-④-0-③（或关键工作为A、C、H、J）和①-③-⑥-⑦-8（或关键工作为B、F、J）。工期：（98-2-2-1）天=93天。最低综合费用=（401+4+7+4）万元=416万元。

  • 第11题：

    某分部工程如下表所示：请绘制双代号网络图。


    答案：
    解析：

  • 第12题：

    已知某施工项目的计划数据资料如下表所示，则第3周的施工成本计划值是（　　）万元。


    A . 30
    B . 90
    C . 60
    D . 75

    答案：B
    解析：
    第3周有土方开挖，混凝土垫层以及混凝土基础，三者相加为15+15+60=90
    第2016版教材P94

  • 第13题：

    已知某工程网络计划如下图所示，该工程工作 E 的最迟开始时间是（　）。（单位为：天）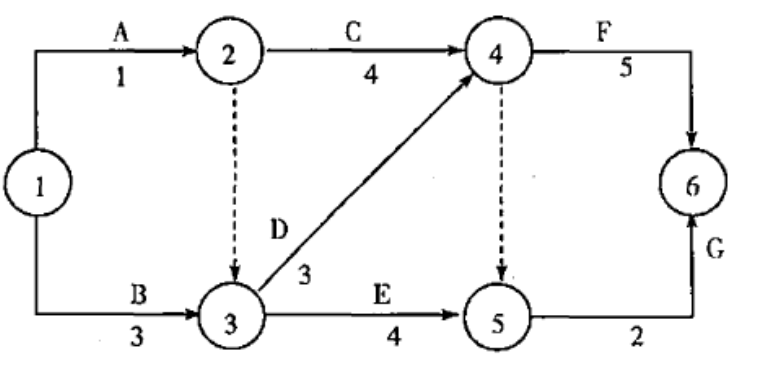

    A.3
    B.5
    C.6
    D.7

    答案：B
    解析：
    本题考查的是制定进度计划的方法。关键线路为 B－D－F，或①－③－④－⑥。总工期为11 天。故 LFG＝11，LSG＝11－2＝9；LFE＝9，LSE＝9－4＝5。

  • 第14题：

    某分部工程单代号网络计划如下图所示，其对应的双代号网络计划应是（ ）。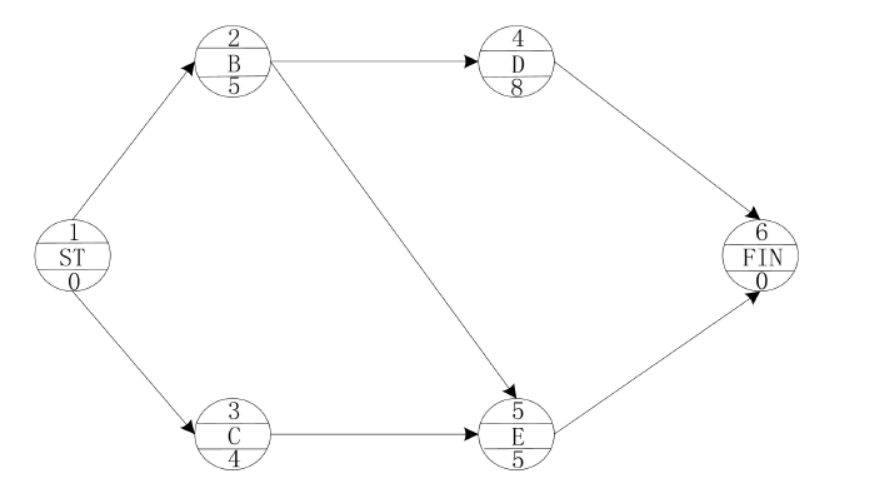



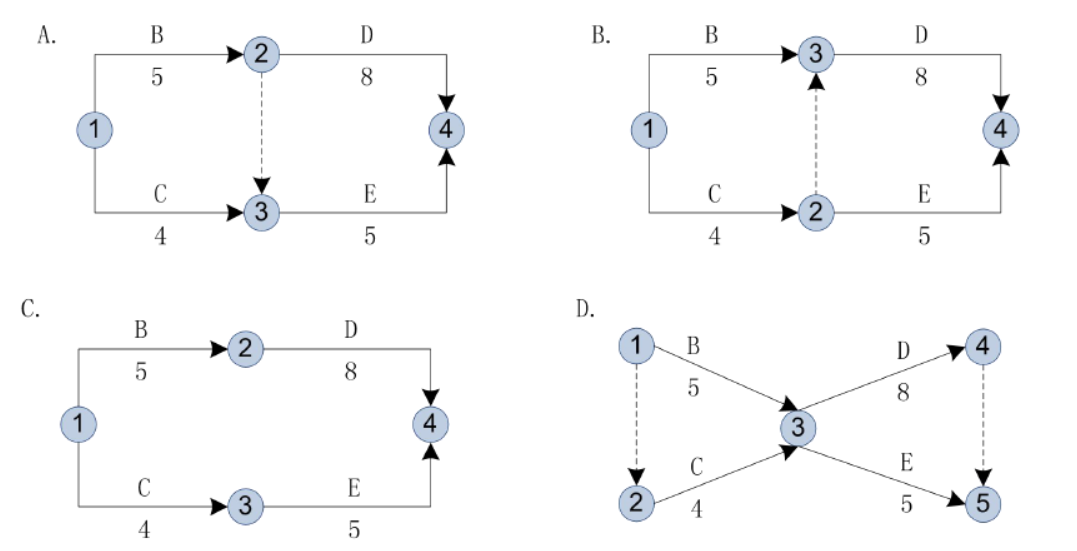    答案：A
    解析：

  • 第15题：

    某监理单位承担了某项目土建工程的施工监理任务，已知该项目相关资料如下表所示。

    该监理单位配备监理人员时所依据的工程建设强度应为()万元/月。

    A:750
    B:600
    C:500
    D:400

    答案：C
    解析：
    工程建设强度是指单位时间内投入的建设工程资金的数量，用公式表示为：工程建设强度=投资/工期，即该监理单位配备监理人员时所依据的工程建设强度：6000/12=500（万元/月）。

  • 第16题：

    已知某施工项目的计划数据资料如下表所示，则第3周的施工成本计划值是（ ）万元。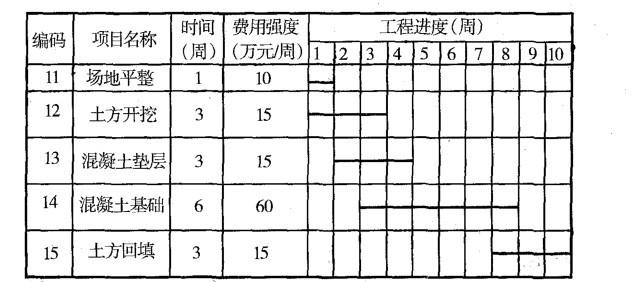


    A.30 B. 60
    C.75 D. 90


    答案：D
    解析：
    如题表中所示，第三周的工作进度涉及土方开挖、混凝土垫层和混凝土基础三项工作，其费用强度分别为15万元/周.、15万元/周、60万 元/周，所以本周的施工成本计划值为：15 + 15 + 60 = 90(万元）。

  • 第17题：

    某分部工程双代号网络计划如下图所示，根据下表给定的逻辑关系和双代号网络计划的绘图规则，其作图错误问题是（　　）。



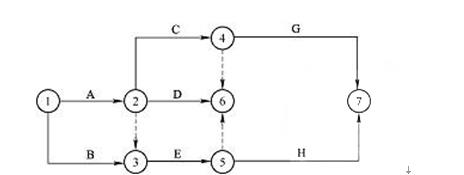
    A、节点编号不对
    B、逻辑关系不对
    C、有多个起点节点
    D、有多个终点节点

    答案：D
    解析：
    2018新教材P137：(7)双代号网络图中应只有一个起点节点和一个终点节点（多目标网络计划除外），而其他所有节点均应是中间节点。而图中有6和7两个终点，选D

  • 第18题：

    已知某分部工程的进度计划如图3所示单代号网络计划。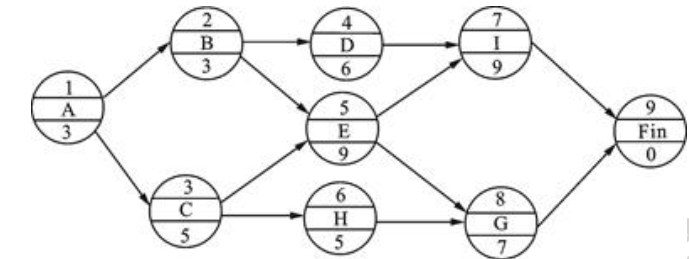

    根据以上资料，回答下列问题：
    该分部工程进度计划的计算工期为（）天。

    A.20
    B.22
    C.24
    D.26

    答案：D
    解析：
    计算工期，是根据网络计划时间参数计算而得到的工期，用TC表示。在单代号网络计划中，TC等于网络计划的终点节点n的最早完成时间EFn，即TC=EFn。本案例中，该分部工程进度计划的计算工期为：TC=3+5+9+9=26（天）。

  • 第19题：

    已知某分部工程的进度计划如图3所示单代号网络计划。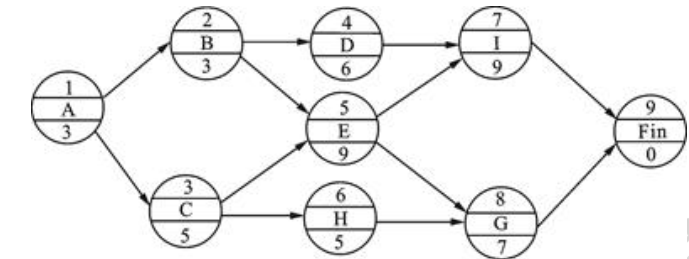

    根据以上资料，回答下列问题：
    工作B的总时差为（）。

    A.2
    B.4
    C.5
    D.7

    答案：A
    解析：

  • 第20题：

    已知某分部工程的进度计划如图3所示单代号网络计划。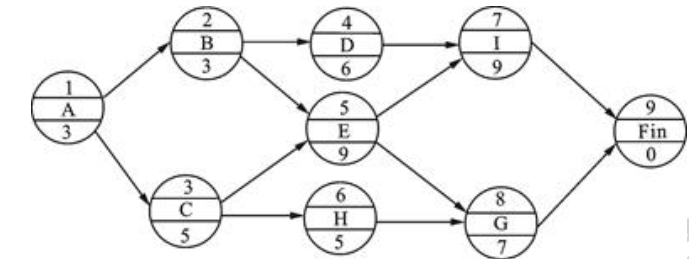

    根据以上资料，回答下列问题：
    工作H的最早完成时间为第（)天。

    A.11
    B.12
    C.13
    D.14

    答案：C
    解析：
    单代号网络图中，工作的最早开始时间等于该工作的各个紧前工作的最早完成时间的最大值。工作的最早完成时间等于该工作的最早开始时间加上其持续时间。则各工作最早开始时间与最早完成时间为：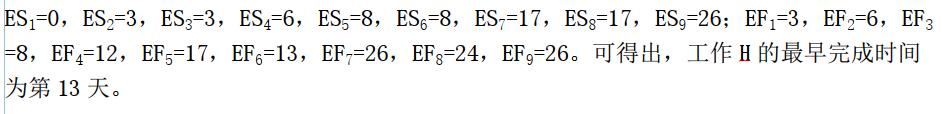

  • 第21题：

    背景已知某工程的网络计划中相关资料如下表所示。



    问题(1)根据上表中相关资料绘制网络图；(2)计算总工期，以及网络图中各工作的六个时间参数（ES、EF,LS,LF,TF,FF）；(3)找出关键线路，并在图中用双箭线标明。


    答案：
    解析：
    (1)绘制网络图如下：



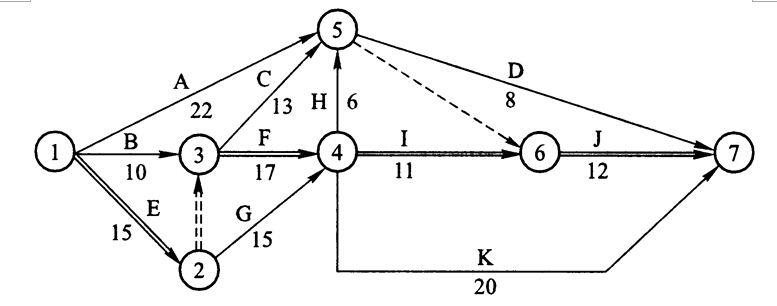
    (2)计算各工作时间参数：总工期T=55。
    1)计算各工作的ES、EF：ESA=0,EFA=22;ESB=0，EFB=10;ESE=0,EFE=15；ESC=15,EFC=28;ESF=15,EFF=32；ESG=15,EFG=30;ESH=32,EFH=38；ESI=32,EFI=43；ESK=32,EFK=52；。ESD=38,EFD=46；ESJ=43,EFJ=55。
    2)计算各工作的LS、LF:LFJ=55，LSJ=43;LFD=55,LSD=47;LFK=55,LSK=35;LFI=43,LSI=32;LFH=43,LSH=37;LFG=32,LSG=17;LFF=32,LSF=15;LFC=43,LSC=30;LFE=15,LSE=0;LFB=15,LSB=5；LFA=43,LSA=21。
    3)计算各工作的TF、FF:TFA=LSA-ESA=21-O=21,FFA=min(ESJ,ESD)-EFA=38-22=16;TFB=LSB-ESB=5-O=5，FFB=min(ESC,ESF)-EFB=15-10=5；TFC=LSC-ESC=30-15=15,FFC=min(ESJ，ESD)-EFC=38-28=10；TFD=LSD-ESD=47-38=9,FFD=T-EFD=55-46=9;TFE=LSE-ESE=0-0=O,FFE=min(ESC,ESF,ESG)-EFE=15-15=O;TFF=LSF-ESF=15-15=0,FFE=min(ESH,ESI,ESK)-EFF=32-32=O;TFG=LSG-ESG=17-15=2,FFG=min(ESH,ESI,ESK)-EFG=32-30=2;TFH=LSH-ESH=37-32=5,FFH=min(ESJ,ESD)-EFH=38-38=0;TFI=LSI-ESI=32-32=0,FFI=ESJ-EFI=43-43=O;TFJ=LSJ-ESJ=43-43=0，FFI=T-EFJ=55-55=0;TFK=LSK-ESK=35-32=3,FFK=T-EFK=55-52=3。
    (3)关键线路：E→F→I→J（或①→②→③→④→⑥→⑦）。

  • 第22题：

    某施工单位编制的某工程网络进度计划图，如下图所示。该网络进度计划原始方案各工作的持续时间和估计费用，见下表。
    【问题】1.根据上述工程网络图，确定网络进度计划原始方案的关键线路和计算工期。


    答案：
    解析：
    1.关键线路：①-③-⑥→⑦-③（或关键工作为B、F、J）。计算工期：98天。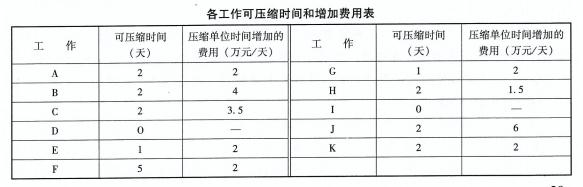

  • 第23题：

    已知某投资项目各年的有关资料如下表所示：

    要求：计算该项目的内含报酬率。


    答案：
    解析：
    NPV=500×（P/F，i，1）＋400×（P/F，i，2）+300×（P/F，i，3）+100×（P/F，i，4）-1000=0
    采用试误法（逐步测试法）：
    （1）使用15%进行测试：NPV=-8.33
    （2）使用14%进行测试：NPV=8.08
    经过以上试算，可以看出该方案的内含报酬率在14%～15%之间。采用内插法确定：

    解之得：IRR=14.49%

相关内容