一个只经营客房的旅馆每间客房的平均售价为50美元,每售出一间客房的变动成本是lo美元。如果该月企业的固定成本是20000美元,则该月的保本点将是:()A、售出200间客房B、售出400间客房C、售出500间客房D、不能从给定信息中确定
题目
A、售出200间客房
B、售出400间客房
C、售出500间客房
D、不能从给定信息中确定
相似考题
参考答案和解析
更多“一个只经营客房的旅馆每间客房的平均售价为50美元,每售出一间客房的变动成本是lo美元。如果该月企业的固定成本是20000美元,则该月的保本点将是:() ”相关问题
-
第1题:
某酒店共有500间客房,每间客房门市价为100美元,某天实际销售了350间客房,平均销售房价为80美元,其收益率为( )。A.75% B.66.7% C.56% D.53%答案:C解析: -
第2题:
42、出售10间客房,每间房费20美元的情况下和出售5间客房,每间房费40美元的情况下,酒店的收益是一样的。
错误 -
第3题:
出售10间客房,每间房费20美元的情况下和出售5间客房,每间房费40美元的情况下,酒店的收益是一样的。
错误 -
第4题:
一个星级旅馆有150个房间。经过一段时间的经营实践,经理得到数据:如果每间客房定价为160元,住房率为55%;如果每间客房定价为140元,住房率为65%;如果每间客房定价为120元,住房率为75%;如果每间客房定价为100元,住房率为85%。欲使每天收入提高,问每间住房的定价应是多少?如果为了便于管理,那么定价140元也是可以的,因为这时它与最高收入只差18.75元。
(1)弄清实际问题加以化简。
经分析,为了建立旅馆一天收入的数学模型,可作如下假设:
①设每间客房的最高定价为160元;
②根据题中提供的数据,设随着房价的下降,住房率呈线性增长;
③设旅馆每间客房定价相等。
(2)建立数学模型。
根据题意,设y表示旅馆一天的总收入,x为与160元相比降低的房价。
由假设②,可得每降低1元房价,住房率增加为 10%/20=0.005因此一天的总收入为y=150(160-x(0.55+0.005x))
由于0.55=0.005x≦1,可知0≦x≦90.
于是问题归结为:当0≦x≦90时,求y的最大值点,即求解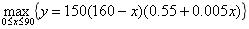
(3)模型求解。
将左边除以(150×0.005)得y’=-x2+50x+17600
由于常数因子对求最大值没有影响,因此可化为y’求的最大值点。利用配方法得y’=-(x-25)2+18225
已知当x=25时y’最大,因此可知最大收入对应的住房定价为160元-25元=135元
相应的住房率为0.55+0.005×25=67.5%最大收入为150×135×67.5%=13668.75(元)
(4)检验。
容易验证此收入在已知各种客房定价的对应收入中确实是最大的,这可从下面表格中看出。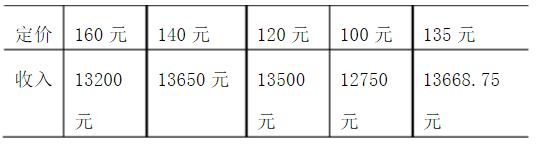
如果每间客房定价为180元,住房率为45%,其相应收入只有12150元。由此可见假设①是合理的。实际上二次函数在[0,90]之内只有一个极值点。
略 -
第5题:
33、以下关于酒店业的说法,正确的是:
A.如接近午夜12点时,酒店决定将客房出售与否的条件是MR>MC
B.当MR<MC时,酒店不可能在此价格下出售某一间客房
C.酒店业的市场结构接近于完全竞争市场结构
D.出售10间客房,每间房费20美元的情况下和出售5间客房,每间房费40美元的情况下,酒店的收益是一样的
如接近午夜12点时,酒店决定将客房出售与否的条件是MR>MC;当MR