设某产品使用寿命X服从正态分布,要求平均寿命不低于1000小时,现从一批这种产品中随机抽出25只,测得平均寿命为950小时,方差为100小时,检验这批产品是否合格可用()。A、t检验法B、χ2检验法C、Z检验法D、F检验法

题目
设某产品使用寿命X服从正态分布,要求平均寿命不低于1000小时,现从一批这种产品中随机抽出25只,测得平均寿命为950小时,方差为100小时,检验这批产品是否合格可用()。

A、t检验法

B、χ2检验法

C、Z检验法

D、F检验法

相似考题

1.为获得某批日光灯产品平均寿命数据，现随机从中抽取100件产品，测得平均寿命为2000小时，则样本平均数为（ ）。A.100小时B.2000小时C.1900小时D.2100小时

2.某超市欲从深圳某公司购进一批净水器，为了检验该产品的质量，超市随机抽取25件净水器进行使用寿命的测试，产品的使用寿命服从正态分布，测得结果如下，平均使用寿命为1061小时，标准差为66．96小时。该超市要求以95%的置信水平估计该批净水器使用寿命的置信区间。

3.一批产品的不合格品率为0.2，现从这批产品中随机取出5个，记X为这5个产品中的不合格品数，则这5个产品中没有不合格品的概率为( )。

4.一批产品的不合格品率为0.2,现从这批产品中随机抽取5个,记X为这5个产品中的不合格品数,则这5个产品中没有合格品的概率为________。A．B．C．D．

更多“设某产品使用寿命X服从正态分布,要求平均寿命不低于1000小时,现从一批这种产品中随机抽出25只,测得平均寿命为950小时,方差为100小时,检验这批产品是否合格可用()。 ”相关问题

  • 第1题：

    某种元件使用寿命X～N（μ,10^2）.按照客户要求该元件使用寿命不能低于1000h,现从该批产品中随机抽取25件,其平均使用寿命为x=995,在显著性水平α=0.05下确定该批产品是否合格？


    答案：
    解析：
    令H0：μ≥1 000,H1小于1 000.因为总体方差已知，所以选取统计量～N(o，1)，
    左临界点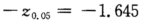为，因为=-2.5小于-1.645，所以拒绝H0，即该批产品不合格.

  • 第2题：

    某超市欲从深圳某公司购进一批净水器，为了检验该产品的质量，超市随机抽取25件净水器进行使用寿命的测试，产品的使用寿命服从正态分布，测得结果如下，平均使用寿命为1061小时，标准差为66．96小时。该超市要求以95％的置信水平估计该批净水器使用寿命的置信区间。


    答案：
    解析：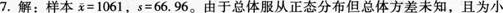

  • 第3题：

    从一批灯泡中随机抽取20只作为样本，测得平均寿命为1900小时，样本标准差为490小时，试在显著性水平0.01下检验该批灯泡平均寿命是否为2000小时？


    H 0 ：μ 1 ＝μ 2 H 1 ：μ 1 ≠μ 2 (双侧检验) 对α＝0．01df＝n 1 ＋n 2 －2＝43查表得[*401]≈2．57因为｜f｜＝3．81＞2．57＝ P＜0．01所以拒绝H 0 认为两批灯泡使用时数的总体均数有极显著差异。 H0：μ1＝μ2,H1：μ1≠μ2(双侧检验) 对α＝0．01,df＝n1＋n2－2＝43,查表得[*401]≈2．57,因为｜f｜＝3．81＞2．57＝ ,P＜0．01,所以拒绝H0认为两批灯泡使用时数的总体均数有极显著差异。

  • 第4题：

    某厂生产某种产品,正常生产时,该产品的某项指标服从正态分布N(50,3.8^2),在生产过程中为检验机器生产是否正常,随机抽取50件产品,其平均指标为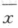=51.26（设生产过程中方差不改变）,在显著性水平为a=0.05下,检验生产过程是否正常.


    答案：
    解析：
    令H0：μ=50，H1：μ≠50，取统计量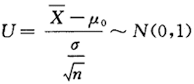，当α=0.05时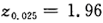，，H0的接受域为(-1.96，1.96)，因为，所以在显著性水平为α=0.05下H0被拒绝，即生产过程不正常.

  • 第5题：

    一批产品的不合格品率为0. 2，现从这批产品中随机取出5个，记X为这5个产品中的不合格品数，则这5个产品中没有不合格品的概率为（ ）。



    答案：B
    解析：

相关内容