下面命题的判断正确的是Ⅰ.完全图Kn(n≥1)都是哈密尔顿图;Ⅱ.完全二部图Kn.m(n≥1,m≥1)都是欧拉图;Ⅲ.任何平面图G的对偶图G*的对偶图G**与G同构。A.只有Ⅰ和Ⅱ为真B.只有Ⅲ为真C.只有Ⅱ为假D.全为假
题目
下面命题的判断正确的是
Ⅰ.完全图Kn(n≥1)都是哈密尔顿图;
Ⅱ.完全二部图Kn.m(n≥1,m≥1)都是欧拉图;
Ⅲ.任何平面图G的对偶图G*的对偶图G**与G同构。
A.只有Ⅰ和Ⅱ为真
B.只有Ⅲ为真
C.只有Ⅱ为假
D.全为假
相似考题
更多“下面命题的判断正确的是 Ⅰ.完全图Kn(n≥1)都是哈密尔顿图; Ⅱ.完全二部图Kn.m(n≥1,m≥1)都是欧拉 ”相关问题
-
第1题:
任意的n阶无向简单图的边数m应满足
A.m≤n-1
B.m≤n(n-1)/2
C.m≤n
D.m≥n
正确答案:B
-
第2题:
n个结点的完全有向图含有边的数目( )。
A、n*n
B、n(n+1)
C、n/2
D、n*(n-l)
正确答案:D
-
第3题:
在图4-14中,(39)是非简单图,(40)是完全图,(41)和(42)都是哈密尔顿图,其中(41)又是欧拉图,(43)是树。
 正确答案:B
正确答案:B
B -
第4题:
具有n个顶点的完全有向图的弧数为()。
A.n(n-1)/2
B.n(n-1)
C.n2
D.n2-1
正确答案:B
-
第5题:
阅读以下说明和流程图,回答问题1-2,将解答填入对应的解答栏内。
[说明]
下面的流程图采用欧几里得算法,实现了计算两正整数最大公约数的功能。给定正整数m和 n,假定m大于等于n,算法的主要步骤为:
(1)以n除m并令r为所得的余数;
(2)若r等于0,算法结束;n即为所求;
(3)将n和r分别赋给m和n,返回步骤(1)。
[流程图]
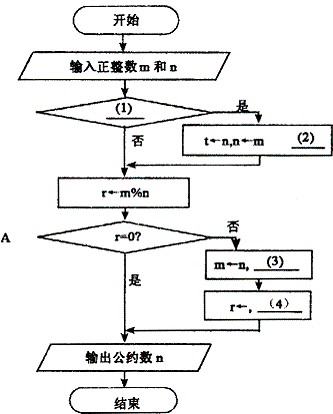
[问题1] 将流程图中的(1)~(4)处补充完整。
[问题2] 若输入的m和n分别为27和21,则A中循环体被执行的次数是(5)。
正确答案:[问题1] (1) n>m或nm或其它等效形式 (2) m←t (3) n←r (4) m%n [问题2] (5) 1
[问题1] (1) n>m或nm或其它等效形式 (2) m←t (3) n←r (4) m%n [问题2] (5) 1 解析:(1)~(2)当n的值大于(等于)m时,应交换两者的值,再使用欧几里得算法;
(3)~(4)略;
(5)m,n和r在执行循环A前后的值分别为: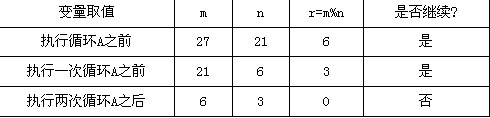
-
第6题:
下列命题正确的是(58)。
A.G为n阶无向连通图,如果G的边数m≥n-1,则G中必有圈
B.二部图的顶点个数一定是偶数
C.若无向图C的任何两个不相同的顶点均相邻,则G为哈密尔顿图
D.3-正则图的顶点个数可以是奇数,也可以是偶数
正确答案:C
解析:n阶无向连通图至少有n-1条边,但n阶无向连通图不一定有圈,所以A错误。二部图顶点个数也可以为奇数,可知D错误。由握手定理可知,n阶k-正则图中,边数m=kn/2,因而当k为奇数时,n必为偶数。所以D错误。所以选C。 -
第7题:
下面除了哪一项之外都是可能正确的?
A.J跑第1圈。
B.M跑第4圈。
C.N跑第1圈。
D.N和P跑第3圈。
正确答案:C
解析:由表格可知,N只能跑第3圈。 -
第8题:
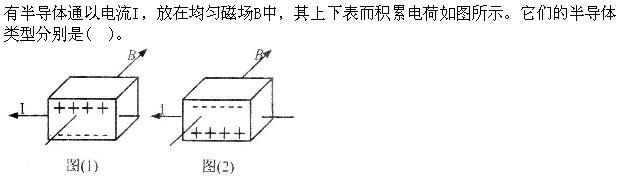 A.图(1)是P型,图(2)是N型
A.图(1)是P型,图(2)是N型
B.图(1)是N型,图(2)是N型
C.图(1)是P型,图(2)是P型
D.图(1)是N型,图(2)是P型答案:D解析:P型半导体为空穴型半导体空穴为多子,自由电子为少子,主要靠空穴导电;N型半导体为电子型半导体,自由电子为多子,空穴为少子,主要靠自由电子导电。由带电粒子在磁场和电场共同作用中的运动可知选D。 -
第9题:
具有n个顶点的有向完全图有() 条弧。
- A、n
- B、n*(n-1)
- C、n*(n+1)
- D、n*n
正确答案:B -
第10题:
具有n个顶点的无向完全图,边的总数为()条。
- A、n-1
- B、n
- C、n+1
- D、n*(n-1)/2
正确答案:D -
第11题:
单选题具有n个顶点的有向完全图有() 条弧。An
Bn*(n-1)
Cn*(n+1)
Dn*n
正确答案: A解析: 暂无解析 -
第12题:
单选题具有n个顶点的无向完全图,边的总数为()条。An-1
Bn
Cn+1
Dn*(n-1)/2
正确答案: C解析: 暂无解析 -
第13题:
设G是n个顶点的无向简单图,则下列说法不正确的是()A、若G是树,则其边数等于n-1
B、若G是欧拉图,则G中必有割边
C、若G中有欧拉路,则G是连通图,且有零个或两个奇度数顶点
D、若G中任意一对顶点的度数之和大于等于n-1,则G中有汉密尔顿路
参考答案:D
-
第14题:
设无向图G中顶点数为n,图G最多( )有条边。A: n
B: n-1
C: n*(n-1)/2
D: n*(n-1)
正确答案: A
-
第15题:
下面程序的运行结果是( )。 includemain() {int a,s,n,m; a=2;s=0;n=1;m=1; while(m<=4 下面程序的运行结果是( )。 include<stdio.h> main() {int a,s,n,m; a=2;s=0;n=1;m=1; while(m<=4){n=n*a;s=s+n;++m;} printf("s=%d",s); }
正确答案:s=30
s=30 解析:分析循环条件“m=1,m=4”,所以循环4次。第1次:n=n*a=2,s=s+n=2;m=2。第2次:n=n*a=4,s=s+n=6;m=3。第3次:n=n*a=8,s=s+n=14;m=4。第4次:n=n*a=16,s=s+n=30。 -
第16题:
设无向图的顶点数为n,则该图最多有()条边。
A.n-1
B.n(n-1)/2
C.n(n+1)/2
D.0
正确答案:B
-
第17题:
在具有n个顶点的完全图Kn中删去(59)边才能得到树?
A.n(n-1)/2
B.(n-1)×(n-2)/2
C.n(n-2)/2
D.n/2
正确答案:B
解析:n个顶点的完全图K,中共有n×(n-1)/2条边,n个顶点的树应有n-1条边,于是,删去的边有:n×(n-1)/2-(n-1)=(n-1)×(n-2)/2 -
第18题:
下面命题的判断正确的是( )。
Ⅰ.完全图Kn(n≥1)都是哈密尔顿图
Ⅱ.完全二部图Kn,m(n≥1,m≥1)都是欧拉图
Ⅲ.任何平面图G的对偶图G*的对偶图G**与G同构
A.只有Ⅰ和Ⅱ为真
B.只有Ⅲ为真
C.只有Ⅱ为假
D.全为假
正确答案:D
-
第19题:
剪力单位是( )、弯矩的单位是( )。A.N或kN,N或kN
B.N.m或kN.m,N.m或kN.m
C.N或kN,N.m或kN.m
D.N.m或kN.m,N或kN答案:C解析:能够使材料产生剪切变形的力称为剪力或剪切力,单位是N或KN。弯矩是受力构件截面上的内力矩的一种,即垂直于横截面的内力系的合力偶矩,单位是N.m或kN.m -
第20题:
关于压强的说法正确的是()。
- A、1Pa=1kg/(s*s*m)
- B、1Pa=1kN/m
- C、1Pa=1N/(s*s)
- D、1Pa=1N/(s*m)
正确答案:A -
第21题:
某完全有向图G含有n个结点,则它含有边的数目()。
- A、(n-1)n/2
- B、n(n+1)
- C、n/2
- D、n(n-l)
正确答案:D -
第22题:
n个结点的完全有向图含有边的数目()。
- A、n*n
- B、n(n+1)
- C、n/2
- D、n(n-1)
正确答案:D -
第23题:
单选题n个结点的完全有向图含有边的数目()。An*n
Bn(n+1)
Cn/2
Dn(n-1)
正确答案: A解析: 暂无解析
