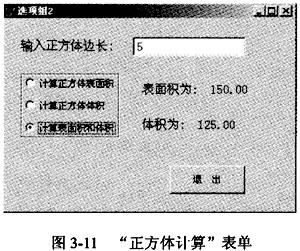
输入正方体的边长，利用“选项”按钮，选择计算表面积、体积等。要求初始时不显示label2 (“表面积为”)和label3(“体积为”)，一旦输入新数据，立即根据选项组的选择显示相应结果，当选择计算表面积时，不出现体积项，同样，选择显示体积时，不显示表面积项。表单样式如图3-11所示。
题目
输入正方体的边长，利用“选项”按钮，选择计算表面积、体积等。要求初始时不显示label2 (“表面积为”)和label3(“体积为”)，一旦输入新数据，立即根据选项组的选择显示相应结果，当选择计算表面积时，不出现体积项，同样，选择显示体积时，不显示表面积项。表单样式如图3-11所示。
相似考题
参考答案和解析
正确答案：操作步骤如下：
①在表单中创建3个“标签”控件、一个“文本框”控件、1个“单选组”和一个“命令按钮”控件并选择好位置和大小。
②设置控件的字体和字号。
③表单控件的主要属性见表3-4。
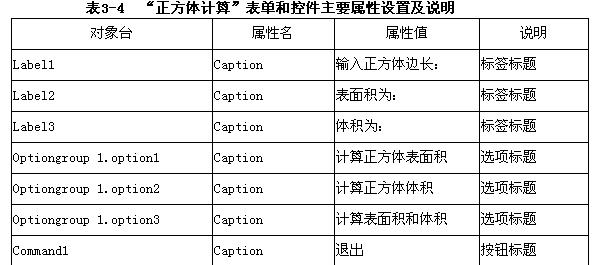④打开“代码编辑”窗口添加Text1的LostFocus事件代码如图3-12所示。
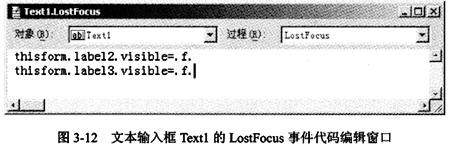⑤添加“选项组”Optiongroup1的Click事件代码如图3-13所示。
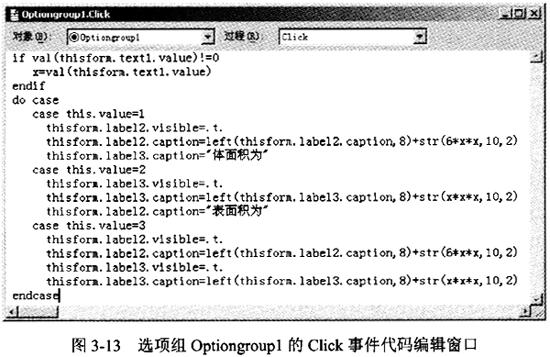⑥添加“退出”按钮Command1的Click事件代码如图3-14所示。
操作步骤如下： ①在表单中创建3个“标签”控件、一个“文本框”控件、1个“单选组”和一个“命令按钮”控件，并选择好位置和大小。 ②设置控件的字体和字号。 ③表单控件的主要属性见表3-4。
④打开“代码编辑”窗口，添加Text1的LostFocus事件代码，如图3-12所示。
⑤添加“选项组”Optiongroup1的Click事件代码，如图3-13所示。
⑥添加“退出”按钮Command1的Click事件代码，如图3-14所示。
④打开“代码编辑”窗口添加Text1的LostFocus事件代码如图3-12所示。
⑤添加“选项组”Optiongroup1的Click事件代码如图3-13所示。
⑥添加“退出”按钮Command1的Click事件代码如图3-14所示。
操作步骤如下： ①在表单中创建3个“标签”控件、一个“文本框”控件、1个“单选组”和一个“命令按钮”控件，并选择好位置和大小。 ②设置控件的字体和字号。 ③表单控件的主要属性见表3-4。
④打开“代码编辑”窗口，添加Text1的LostFocus事件代码，如图3-12所示。
⑤添加“选项组”Optiongroup1的Click事件代码，如图3-13所示。
⑥添加“退出”按钮Command1的Click事件代码，如图3-14所示。
更多“ 输入正方体的边长，利用“选项”按钮，选择计算表面积、体积等。要求初始时不显示label2 (“表面积为”)和label3(“体积为”)，一旦输入新数据，立即根据选项组的选择显示相应结果，当选择计算表面积时，不出现”相关问题
-
第1题：
在棱长为1的正方体上切下两个角，所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体，六面体体积为原正方体体积的1/24，则六面体表面积为原正方体表面积的：A.1/4
B.1/6
C.1/8
D.1/10答案：C解析：由题意知切下的角是底面为正三角形、侧面为三个等腰直角三角形的三棱锥，设切下角的直角边为ｘ，则六面体体积＝2×三棱锥体积＝2×(1/3)×(ｘ2/2)×ｘ＝1/24，解得ｘ＝1/2。所以六面体每个面是直角边为1/2的等腰直角三角形，六面体的每个面相当于边长为1的正方形面积的1，所以六面体的表面积为原正方体的1/8。故本题选C。 -
第2题：
表面积为24的长方体中体积最大为（）.
C -
第3题：
【单选题】颗粒表面积为S，体积为V，同体积球体表面积为S0，同表面积球体体积为V0，则球形度φs为
A．S/ S0
B．S0/ S
C．V / V0
D．V0/ V
S0/ S -
第4题：
一个长方体木块恰能切割成五个正方体木块，五个正方体木块表面积之和比原来的长方体木块的表面积增加了200cm2。则长方体木块的体积为多少?A.625cm3
B.125cm3
C.500cm3
D.750cm3答案：A解析：第一步，本题考查几何问题，属于立体几何类。
第二步，如图所示，长方体分为5个小正方体，增加了4×2=8（个）阴影部分小正方形的面积，则每个小正方形面积为200÷8=25（cm2），边长为5cm。那么大长方体的体积为5×25×5=625（cm3）。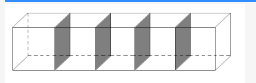
因此，选择A选项。 -
第5题：
编写一个圆柱体类（Cylinder），在该类中添加半径radius，高度height作为属性；提供计算圆柱的表面积getArea，圆柱体积getVolumn方法。另外，编写一个测试类App，运行时，在控制台中提示用户输入圆柱体的半径（radius)和高度（height)；读入用户输入后，显示该圆柱的基本信息和表面积，体积的相关数据
#includeusing namespace std;const double PI=3.141592;class cylinder{public: cylinder (double a,double b) ; void vol () ;private : double r,h; double volume;};cylinder::cylinder (double a, double b){ r=a; h=b; volume= PI*r* r* h;}void cylinder::vol (){ cout}void main(){ int i,n; cylinder *p; double radius,height; cout cin>>n; for(i=0;i { cout cin>>radius>>height; p=new cylinder(radius,height); p->vol(); }}