某二叉树T有n个结点，设按某种顺序对T中的每个结点进行编号，编号值为1、2、…、n，且有如下性质：T中任一结点v，其编号等于左子树上的最小编号减1，而v的右子树的结点中，其最小编号等于 v左子树上的最大编号加1。此二叉树是按( )顺序编号的。A．前序遍历B．中序遍历C．后序遍历D．按层次遍历

题目

某二叉树T有n个结点，设按某种顺序对T中的每个结点进行编号，编号值为1、2、…、n，且有如下性质：T中任一结点v，其编号等于左子树上的最小编号减1，而v的右子树的结点中，其最小编号等于 v左子树上的最大编号加1。此二叉树是按( )顺序编号的。

A．前序遍历

B．中序遍历

C．后序遍历

D．按层次遍历

相似考题

1.（ 12 ） 按层次次序将一棵有 n 个结点的完全二叉树的所有结点从 1 到 n 编号 ， 当 i<n/2 时 ， 编号为 i 的结点的左子女的编号是A ） 2i-1B ） 2iC ） 2i+1D ）不确定

2.（3）按层次次序将一棵有 n 个结点的完全二叉树的所有结点从 1到 n 编号，当 i≤(n-1)/2 时，结点 i 的右子女的结点编号为___________。

3.若按层次顺序将一棵有n个结点的完全二叉树的所有结点从1到n编号，那么当i为偶数且小于n时，结点；的右兄弟是结点【 】，否则结点；没有右兄弟。

4.对n个结点的二叉树,按()遍历顺序对结点编号(号码为1~n)时,任一结点的编号等于其左子树中结点的最大编号加1,又等于其右子树中结点的最小编号减1。A.前根B.中根C.后根D.层次

参考答案和解析
正确答案：A
解析：根据节点v的右子树的结点中，其最小编号等于v左子树上的结点的最大编号加1，可以断定是前序遍历。
更多“某二叉树T有n个结点,设按某种顺序对T中的每个结点进行编号,编号值为1、2、…、n,且有如下性质:T中任 ”相关问题

  • 第1题：

    按层次次序将一棵有n个结点的完全二叉树的所有结点从1到n编号，当i≦(n-1)/2时，编号i的结点的右子女的编号是（ ）。

    A)2i-1

    B)2i

    C)2i+1

    D)不确定


    正确答案：C
    完全二叉树中除最下面一层外，各层都被结点充满了，每一层结点个数恰是上一层结点个数的2倍。因此，从一个结点的编号就可以推知它的双亲及左、右子女结点的编号。当i≤ n/2时，结点i的左子女是结点2i，否则结点i没有左子女。当i≤(n-1)/2时，结点i的右子女是结点2i+1，否则结点i没有右子女。

  • 第2题：

    某二叉树T有n个节点，设按某种顺序对T中的每个节点进行编号，编号值为1，2，… n，且有如下性质：T中任一节点v，其编号等于左子树上的最小编号减1，而v的右子树的节点中，其最小编号等于v左子树上的节点的最大编号加1。此二叉树是按( )顺序编号的。

    A．前序遍历

    B．中序遍历

    C．后序遍历

    D．按层次遍历


    正确答案：A
    解析：根据节点v的右子树的节点中，其最小编号等于v左子树上的节点的最大编号加1，可以断定是前序遍历。

  • 第3题：

    按层次次序将一棵有n个结点的完全二叉树的所有结点从1到n编号，当i≤n/2时，编号i的结点的左子女的编号是________。

    A．2i-1

    B．2i

    C．2i+1

    D．不确定


    正确答案：B
    解析：完全二叉树中除最下面一层外，各层都被结点充满了，每一层结点个数恰是上一层结点个数的2倍。因此，从一个结点的编号就可以推知它的双亲及左、右子女结点的编号。当i ≤ n/2时，结点i的左子女是结点2i，否则结点i没有左子女。当i ≤ (n-1)/2时，结点i的右子女是结点2i+1，否则结点i没有右子女。

  • 第4题：

    一个深度为I(I≥1)的二叉树有n个结点，从1-n对结点自上而下，自左至右编号，这样的树( )。

    A．是完全二叉树

    B．是满二叉树

    C．结点数最多2i1个

    D．父结点编号是子结点编号的1/2


    正确答案：A
    解析：这是完全二叉树的定义，应该注意满二叉树与完全二叉树的区别，满二叉树是完全二叉树，但完全二叉树却不一定为满二叉树。

  • 第5题：

    设F是T1、T2和T3三棵树组成的森林，与F对应的二叉树为B，已知T1、T2和T3的结点个数分别为n1, n2和n3，则二叉树B的根结点左子树和右子树中结点的个数分别为 【】 和 【】


    正确答案：

    n1－1    n2+n3


    树与二叉树的转换；将森林中每棵树的根结点作为二叉树的根结点，每个结点中的从左数第一个孩子是二叉树中的左孩子，该孩子的所有兄弟都依次为该结点的右孩子 ，如此例推

  • 第6题：

    按层次次序将一棵有n-个结点的完全二叉树的所有结点从1～n编号，当i≤n／2时，编号为i的结点的左子树的编号是（ ）。

    A.2i-1

    B.2i

    C.2i+1

    D.不确定


    正确答案：B
    B。【解析】完全二叉树中除最下面一层外，各层都被结点充满了，每一层结点个数恰是上一层结点个数的2倍。因此，从一个结点的编号就可推知它的双亲及左、右子树结点的编号。当i≤n／2时，编号为i的结点的左子树的编号是2i，否则结点i没有左子树。当i≤(n-1)／2时，编号为i的结点的右子树的编号是2i+1，否则结点i没有右子树。当i≠1时，编号为i的结点的双亲是结点i／2。

  • 第7题：

    对二叉树中的结点如下编号：树根结点编号为1，根的左孩子结点编号为2、右孩子结点编号为3，依此类推，对于编号为i的结点，其左孩子编号为2i、右孩子编号为2i+1。例如，下图所示二叉树中有6个结点，结点a、b、c、d、e、f的编号分别为1、2、3、5、7、11。那么，当结点数为n（n>0）的（ ）时，其最后一个结点编号为2i-1

    A.二叉树为满二叉树（即每层的结点数达到最大值）B.二叉树中每个内部结点都有两个孩子C.二叉树中每个内部结点都只有左孩子D.二叉树中每个内部结点都只有右孩子


    正确答案：C

  • 第8题：

    在一棵完全二叉树的顺序存储方式中，若编号为t的结点有右孩子，则此结点右孩子的编号为( )

    A．2t

    B．2t-1

    C．2t+1

    D．t/2


    正确答案：C

  • 第9题：

    按层次次序将一棵有n个结点的完全二叉树的所有结点从1到n编号，当i≤（n-1）/2时，结点i的右子女的结点编号为（）。


    正确答案:2i+1

  • 第10题：

    设F是由T1、T2和T3三棵树组成的森林，与F对应的二叉树为B，T1、T2和T3的结点数分别为N1、N2和N3，则二叉树B的根结点的左子树的结点数为（）

    • A、N1-1
    • B、N2-1
    • C、N2+N3
    • D、N1+N3

    正确答案:A

  • 第11题：

    一棵深度为H的满k叉树有如下性质：第H层上的结点都是叶子结点，其余各层上每个结点都有k棵非空子树，如果按层次自上至下，从左到右顺序从1开始对全部结点编号，回答下列问题：编号为n的结点有右兄弟的条件是什么？其右兄弟的编号是多少？


    正确答案:编号为n的结点有右兄弟的条件是(n-1)%m≠0。其右兄弟的编号是n+1。

  • 第12题：

    单选题
    设F是由T1、T2和T3三棵树组成的森林，与F对应的二叉树为B，T1、T2和T3的结点数分别为N1、N2和N3，则二叉树B的根结点的左子树的结点数为（）
    A

    N1-1

    B

    N2-1

    C

    N2+N3

    D

    N1+N3


    正确答案： D
    解析： 暂无解析

  • 第13题：

    设F是由T1、T2和T3三棵树组成的森林，与F对应的二叉树为B，已知T1、T2和T3的结点个数分别为n1、n2和n3，则二叉树B的根结点左子树个数为（ ）。

    A)1

    B)n1-1

    C)n3

    D)n2+n3


    正确答案：B
    由森林到二叉树的转换可知，森林F中第一棵树的根转换得到的二叉树的根，T1其他结点均在B的根结点的左子树中，而T2、T3的结点均在右子树中。所以左子树个数是n1-1。 

  • 第14题：

    按层次次序将一棵有n个结点的完全二叉树的所有结点从1到n编号，当i≤n／2时，编号为i的结点的左子女的编号为

    A．2i-1

    B．2i

    C．2i+l

    D．不确定


    正确答案：B
    解析：根据二叉树的性质可以知道，如果对一棵有n个结点的完全二叉树的结点按层序编号，则对任意结点i(1≤i≤n)有：如果i=1，则结点i是二叉树的根，无双亲；如果i>l，则双亲PARENT(i)是结点V2。如果2i>n，则结点i无左孩子；否则其左孩子结点是2i。如果2i+1>n，则结点i无右孩子；否则其右孩子是结点2i+l。本题答案为B)。

  • 第15题：

    某二叉树T有n个结点，设按某种顺序对T中的每个结点进行编号，编号值为1,2…,n，且有如下性质：T中任一结点v，其编号等于左子树上的最小编号减1，而v的右子树的结点中，其最小编号等于v左子树上的结点的最大编号加1。此二叉树是按( )顺序编号的。

    A．前序遍历

    B．中序遍历

    C．后序遍历

    D．按层次遍历


    正确答案：A
    解析：根据结点v的右子树的结点中，其最小编号等于v左子树上的结点的最大编号加 1，可以断定是前序遍历。

  • 第16题：

    具有n个结点的完全二叉树，若按自上而下、从左到右依次给结点编号，则编号最小的叶结点的序号是（ ）。A．[n/2] B．[n+1］C．［n/2］＋1 D．［n/2］－1


    正确答案：C
    完全二叉树编号最小的叶节点即为最后一层的第一个节点。[n/2]为倒数第二层的最后一个节点，因此结果为[n/2]+1.

  • 第17题：

    一个高度为h的满二叉树的结点总数为2h-1，其每一层结点个数都达到最大值。从根结点开始顺序编号，每一层都从左到右依次编号，直到最后的叶子结点层为止。即根结点编号为1，其左、右孩子结点编号分别为2和3，再下一层从左到右的编号为4、5、6、7，依此类推，那么，在一棵满二叉树中，对于编号为m和n的两个结点，若m=2n，则结点（40）。

    A.m是n的左孩子

    B.m是n的右孩子

    C.n是m的左孩子

    D.n是m的右孩子


    正确答案：A
    在满二叉树中，有两个编号为m和n的节点，其中m=2n，说明m是m的左孩子节点，这就好比编号为1与编号为2的节点关系。

  • 第18题：

    设对一个n个结点的完全二叉树按序的编号为1，2，3…n，若某结点I≤(n-1)/2，则结点 I的右子女为( )。

    A．2i-1

    B．2i

    C．2i+1

    D．I+1


    正确答案：C
    解析：在完全二叉树编号中，若结点有左孩子，则该孩子的编号必为它编号的两倍，相应地若它有右孩子，则其编号比左孩子大1，所以结点I的右子女为2i+1。

  • 第19题：

    按层次次序将一棵有n个结点的完全二叉树的所有结点从1到n编号，当i≤(n－1)/2时，编号i的结点的右子女的编号是（ ）。

    A）2i－1

    B）2i

    C）2i 1

    D）不确定


    正确答案：C

  • 第20题：

    一个高度为h的满二叉树的结点总数为2（h次方）-1其每一层结点个数都达到最大值。从根结点开始顺序编号，即根结点编号为1，其左、右孩子结点编号分别为2和3，再下一层从左到右的编号为4、5、6、7，依次类推，每一层都从左到右依次编号，直到最后的叶子结点层为止。那么，在一颗满二叉树中，对于编号m和n的两个结点，若m=2n+1，则（ ）。

    A.m是n的左孩子
    B.m是n的右孩子
    C.n是m的左孩子
    D.n是m的右孩子

    答案：B
    解析：
    本题考查数据结构基础知识。
    用验证的方法求解，以高度为3的满二叉树（如下图所示）为例进行说明。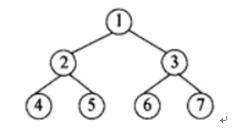

    若m=2n+1，则结点m是n的右孩子结点。

  • 第21题：

    一棵深度为H的满k叉树有如下性质：第H层上的结点都是叶子结点，其余各层上每个结点都有k棵非空子树，如果按层次自上至下，从左到右顺序从1开始对全部结点编号，回答下列问题：编号为n的结点的第i个孩子结点如果存在，编号是多少？


    正确答案:编号为n的结点的第i个孩子结点如果存在，编号是(n-1)*m+i+1。

  • 第22题：

    一棵深度为H的满k叉树有如下性质：第H层上的结点都是叶子结点，其余各层上每个结点都有k棵非空子树，如果按层次自上至下，从左到右顺序从1开始对全部结点编号，回答下列问题：编号为n的结点的父结点如果存在，编号是多少？


    正确答案:编号为n的结点的父结点如果存在，编号是((n-2)/m)+1

  • 第23题：

    填空题
    按层次次序将一棵有n个结点的完全二叉树的所有结点从1到n编号，当i≤（n-1）/2时，结点i的右子女的结点编号为（）。

    正确答案： 2i+1
    解析： 暂无解析

相关内容