在k-means或kNN,我们常用欧氏距离来计算最近的邻居之间的距离,有时也用曼哈顿距离,请对比下这两种距离的差别
题目
在k-means或kNN,我们常用欧氏距离来计算最近的邻居之间的距离,有时也用曼哈顿距离,请对比下这两种距离的差别
相似考题
参考答案和解析
欧氏距离,最常见的两点之间或多点之间的距离表示法,又称之为欧几里得度量,它定义于欧几里得空间中,如点 x = (x1,...,xn) 和 y = (y1,...,yn) 之间的距离为:
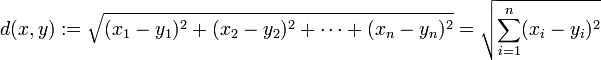
欧氏距离虽然很有用,但也有明显的缺点。它将样品的不同属性(即各指标或各变量量纲)之间的差别等同看待,这一点有时不能满足实际要求。例如,在教育研究中,经常遇到对人的分析和判别,个体的不同属性对于区分个体有着不同的重要性。因此,欧氏距离适用于向量各分量的度量标准统一的情况。曼哈顿距离,我们可以定义曼哈顿距离的正式意义为L1-距离或城市区块距离,也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上,坐标(x1, y1)的点P1与坐标(x2, y2)的点P2的曼哈顿距离为:
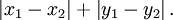
要注意的是,曼哈顿距离依赖座标系统的转度,而非系统在座标轴上的平移或映射。当坐标轴变动时,点间的距离就会不同。通俗来讲,想象你在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。而实际驾驶距离就是这个“曼哈顿距离”,这也是曼哈顿距离名称的来源, 同时,曼哈顿距离也称为城市街区距离(City Block distance)。曼哈顿距离和欧式距离一般用途不同,无相互替代性。
更多“在k-means或kNN,我们常用欧氏距离来计算最近的邻居之间的距离,有时也用曼哈顿距离,请对比下这两 ”相关问题
-
第1题:
K最近邻(KNN)分类器的基本算法步骤包括
A.算距离:给定测试对象,计算它与训练集中的每个对象的距离
B.找邻居:圈定距离最近的k个训练对象,作为测试对象的近邻
C.做分类:根据这k个近邻归属的主要类别,来对测试对象分类
算距离:给定测试对象,计算它与训练集中的每个对象的距离;找邻居:圈定距离最近的k个训练对象,作为测试对象的近邻;做分类:根据这k个近邻归属的主要类别,来对测试对象分类 -
第2题:
4、关于文档向量之间的欧氏距离和余弦相似度,错误的是
A.欧氏距离指在m维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离)
B.余弦相似度,又称为余弦相似性,是通过计算两个向量的夹角余弦值来评估他们的相似度
C.余弦值越接近0,就表明两个向量越相似
D.两个向量之间的欧氏距离越大,则通常其余弦相似度越小
余弦值越接近 0 ,就表明两个向量越相似 -
第3题:
【多选题】常见的距离度量方法包括()
A.欧氏距离
B.汉明距离
C.曼哈顿距离
D.切比雪夫距离
ABCD -
第4题:
以下哪些是距离关系?
A.欧氏距离
B.曼哈顿距离
C.大地测量距离(大地线)
D.旅行时间距离
B -
第5题:
1、下列哪个距离度量不在KNN算法中体现:()。
A.切比雪夫距离
B.欧氏距离
C.余弦相似度
D.曼哈顿距离
D
