用贪婪算法解决背包问题，贪婪准则为：每次都选择价值最大的物品装包。假设n=3；W1=90，V1=60；W2=25，V2=50；W3=20，V3=40；C=100。下列说法不正确的是 （）A．利用价值最大的贪婪准则时，选物品1，这种方案的总价值为60B．最优解选物品为2和3，总价值为90C．就本题而言，使用贪婪准则，不能保证得到最优解D．利用价值最大的贪婪准则时，选物品2和3，总价值为90

题目

用贪婪算法解决背包问题，贪婪准则为：每次都选择价值最大的物品装包。假设n=3；W1=90，V1=60；W2=25，V2=50；W3=20，V3=40；C=100。下列说法不正确的是 （）

A．利用价值最大的贪婪准则时，选物品1，这种方案的总价值为60

B．最优解选物品为2和3，总价值为90

C．就本题而言，使用贪婪准则，不能保证得到最优解

D．利用价值最大的贪婪准则时，选物品2和3，总价值为90

相似考题

1.按国标规定电动机绕组的首端用U1、V1、W1表示，末端用U2、V2、W2表示。()此题为判断题(对，错)。

2.n*n矩阵可看作是n维空间中的线性变换，矩阵的特征向量经过线性变换后，只是乘以某个常数(特征值)，因此，特征向量和特征值在应用中具有重要的作用。下面的矩阵(其中w1、w2、w3均为正整数)有特征向量(w1，w2，w3)，其对应的特征值为( )。A．1／3B．1C．3D．9

3.Given the following DDL and INSERT statements:CREATE VIEW v1 AS SELECT col1 FROM t1 WHERE col1 > 10; CREATE VIEW v2 AS SELECT col1 FROM v1 WITH CASCADED CHECK OPTION; CREATE VIEW v3 AS SELECT col1 FROM v2 WHERE col1 < 100; INSERT INTO v1 VALUES(5); INSERT INTO v2 VALUES(5); INSERT INTO v3 VALUES(20); INSERT INTO v3 VALUES(100);How many of these INSERT statements will be successful?（）A.0B.1C.2D.3

4.1mol单原子理气从298K、202.65kPa经历①等温②绝热③等压三条途径可逆膨胀,体积增加到原来2倍,所作功分别为W1,W2,W3。绝对值大小的关系为:()。A.W3>W2>W1B.W3>W1>W2C.W2>W1>W3D.W1>W2>W3

参考答案和解析
错误
更多“用贪婪算法解决背包问题，贪婪准则为：每次都选择价值最大的物品装包。假设n=3；W1=90，V1=60；W2=25，V2=50；W3=20，V3=40；C=100。下列说法不正确的是 （）”相关问题

  • 第1题：

    0-1背包问题可以描述为：有n个物品，对i=1，2，…，n，第i个物品价值为vi ，重量为wi（vi，和wi为非负数），背包容量为W（W为非负数），选择其中一些物品装入背包，使装入背包物品的总价值最大，，且总重量不超过背包容量，即，其中，xi∈{0,1}，xi=0表示第i个物品不放入背包，xi=1表示第i个物品 放入背包。

    【问题1】（8分）

    用回溯法求解此0-1背包问题，请填充下面伪代码中（1）~（4）处空缺。

    回溯法是一种系统的搜索方法。在确定解空间后，回溯法从根结点开始，按照深度优先策略遍历解空间树，搜索满足约束条件的解。对每一个当前结点，若扩展该结点己经不满足约束条件，则不再继续扩展。为了进一步提高算法的搜索效率，往往需要设计一个限界函数，判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOUND（v,w,k,W）函数，其中v, w, k和W分别表示当前已经获得的价值、当前背包的重量、己经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点，该函数值表示确定了部分物品是否选择之后，对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值，若该价值小于等于当前已经得到的最优解，则该结点无需再扩展。

    下面给出0-1背包问题的回溯算法伪代码。

    函数参数说明如下：

    W：背包容量；n：物品个数；w：重量数组；v：价值数组；fw：获得最大价值时背包的重量；fp：背包获得的最大价值；X：问题的最优解。

    变量说明如下：

    cw：当前的背包重量；cp：当前获得的价值；k：当前考虑的物品编号；Y：当前已获得的部分解。

    BKNAP(W,n,w,v,fw,fp,X）

    1 cw ← cp ← 0

    2 （1）

    3 fp ← -1

    4 while true

    5 while k≤n and cw＋w[k]≤W do

    6 （2）

    7 cp ← cp＋v[k]

    8 Y[k]← 1

    9 k ← k+1

    10 if k＞n then

    11 if fp＜cp then

    12 fp ← cp

    13 fw ← ew

    14 k ← n

    15 X ← Y

    16 else Y(k)← 0

    17 while BOUND(cp,cw,k,W) ≤fp do

    18 while k≠0 and Y(k)≠1 do

    19 （3）

    20 if k＝0 then return

    21 Y[k]←0

    22 cw ← cw ← w[k]

    23 cp ← cp ← v[k]

    24 （4）


    正确答案：

    　本题考查的是用回溯法求解0-1背包问题。回溯法有两类算法框架：非递归形式和递归形式，本题采用非递归形式表示。理解回溯法的基本思想和这两类算法框架是正确解答本题的根本要求·回溯法从第一项物品开始考虑是否应该装入背包中，因此当前考虑的物品编号k从1开始，即k←1。然后逐项往后检查，若能全部放入背包则将该项放入背包，此时背包的重量应该是当前的重量加上当前考虑物品的重量，即cw←cw+w[k]，当然背包中物品的价值也为当前的价值加上当前考虑物品的价值。若己经考虑完了所有的物品，则得到一个解，判断该解是否为当前最优，若为最优，则将该解的信息放入变量fp、fw和X中。若还没有考虑完所有的物品，意味着有些物品不能放入背包，此时先判断若不将当前的物品放入背包中，则其余物品放入背包是否可能得到比当前最优解更优的解，若得不到则回溯；否则继续考虑其余的物品。

    【问题1】（共8分，各2分）

    （1）k ← 1 或其等价形式

    （2）cw ← cw + w[k] 或其等价形式

    （3）k ← k – 1 或其等价形式

    （4）k ← k + l 或其等价形式

  • 第2题：

    考虑一个背包问题，共有n=5个物品，背包容量为W=10，物品的重量和价值分别为：w={2，2，6，5，4}，v={6,3，5，4，6}，求背包问题的最大装包价值。若此为0-1背包问题，分析该问题具有最优子结构，定义递归式为

    其中c(i，j)表示i个物品、容量为j的0-1背包问题的最大装包价值，最终要求解c(n,W)。 采用自底向上的动态规划方法求解，得到最大装包价值为(62)，算法的时间复杂度为(63)。 若此为部分背包问题，首先采用归并排序算法，根据物品的单位重量价值从大到小排序，然后依次将物品放入背包直至所有物品放入背包中或者背包再无容量，则得到的最大装包价值为(64)，算法的时间复杂度为(65)。

    A.11

    B.14

    C.15

    D.16.67


    正确答案：C

  • 第3题：

    如图所示，有一容器，内装互不相溶的两种液体。现将质量及体积皆相同的三个铝块，分别以细绳悬吊于弹簧秤下，使静止于液体中。若弹簧秤的读数分别为W1、W2和W3，则 下列关系正确的是（ ）。（细绳之重量及粗细不计）


    A. W1=W2=W3
    B. W1＞W2=W3
    C. W1＞W2 ＞W3
    D. W1＜W2 =W3

    答案：B
    解析：

  • 第4题：

    阅读下列说明和C代码,回答问题1至问题3,将解答写在答题纸的对应栏内。【说明】0-1背包问题定义为:给定1个物品的价值v[1....i]、重量w[1....i]和背包容量T,每个物品装到背包里或者不装到背包里,求最优的装包方案,使得所得到的价值最大。0-1背创问题具有最优子结构性质,定义c为最优装包方案所获得的最大价值则可得到如下所示的递归式。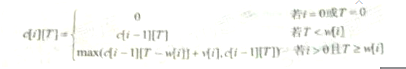

    【C代码】下面是算法的C语言实现(1)常量和变量说明T:背包容量V[]:价值数组W[]:重量数组C[][]:c[i][j]表示前i个物品在背包容量为j的情况下最优装包方案所能获得的最大价值(2)C程序


    【问题1】(8分)根据说明和C代码,填充C代码中的空(1)~(4)【问题2】(4分)根据说明和C代码,算法采用了(5)设计策略。在求解过程中,采用了(6)(自底向上或者自顶向下)的方式。【问题3】(3分)若5项物品的价值数组和重量数组分别为v[]={0,1,6,18,22,28}和w[]={0,1,2,5,6,7},背包容量为T=11,则获得的最大价值为(7)。


    答案：
    解析：
    问题1:1:c[i][j]2: temp

  • 第5题：

    有0-1背包问题如下： n=6，c=20，P=（4，8，15，1，6，3），W=（5，3，2，10，4，8）。 其中n为物品个数，c为背包载重量，P表示物品的价值，W表示物品的重量。请问对于此0-1背包问题，应如何选择放进去的物品，才能使到放进背包的物品总价值最大。 P=（15，8，6，4，3，1），W=（2，3，4，5，8，10），单位重量物品价值（7.5，2.67，1.5，0.8，0.375，0.1）


    正确答案: 可知随着物品的重量增加，物品的价值减少；因此可以用贪心算法来求解。以选取单位重量物品价值高为贪心策略。
    1.先把重量为2的物品放进背包，此时剩余载重量为17，P为15。
    2.把重量为3的物品放进背包，此时剩余载重量为14，P为23；
    3.把重量为4的物品放进背包，此时剩余载重量为10，P为29；
    4.把重量为5的物品放进背包，此时剩余载重量为5，P为33；
    由于8>5，所以不能再放进背包。
    结果是把重量为2，3，4，5的物品装进背包，总价值最大为33。

  • 第6题：

    已知单自由度系统的振动固有频率wn=2rad/s，若在其上分别作用幅值相同而频率为w1=1rad/s；w2=2rad/s，w3=3rad/s的简谐干扰力，则此系统强迫振动的振幅为：（）

    • A、w1=1rad/s时振幅最大
    • B、w2=2rad/s时振幅最大
    • C、w3=3rad/s时振幅最大
    • D、不能确定

    正确答案:B

  • 第7题：

    对于如下描述的背包问题，请计算最终装入背包的最大价值和以及各个物品装入背包的数量。 背包容量：C＝50千克。3件物品。物品1重20千克，价值100元；物品2重20千克，价值120元；物品3重30千克，价值90元。


    正确答案: 物品1的单位重量价值为50元/千克；物品2的单位重量价值为60元/千克；物品3的单位重量价值为30元/千克。采用贪心算法解此背包问题。
    此时，贪心的策略是：每次选择单位重量价值最大的物品。因此，首先选择物品2，然后是物品1，最后是物品3，直至将背包装满。
    物品2全部装入背包，当前背包中价值120元，背包占用20千克，剩余30千克；
    物品1全部装入背包，当前背包中价值220元（120元＋100元），背包占用40千克，剩余10千克；
    物品3的1/3被装入背包，当前背包中价值250元（120元＋100元＋90元×1/3），背包占用50千克（装满）。
    因此，最终装入背包的最大价值为250元，物品1和物品2都全部装入，分别是20千克和20千克，物品3装入1/3，是10千克。

  • 第8题：

    转轮叶片进、出口水流绝对速度，分别用字母（）表示。

    • A、vr1和vr2；
    • B、w1和w2；
    • C、v1和v2；
    • D、v2和v1。

    正确答案:C

  • 第9题：

    自然伽马能谱测井仪送上来的多道数据，在地面被分为五个能窗，简称为W1、W2、W3、W4、W5，低能区的三个窗口为W1、W2、W3，高能区的两个窗口为、W4、W5。


    正确答案:错误

  • 第10题：

    按国标规定电动机绕组的首端用U1、V1、W1表示，末端用U2、V2、W2表示。


    正确答案:正确

  • 第11题：

    问答题
    有0-1背包问题如下： n=6，c=20，P=（4，8，15，1，6，3），W=（5，3，2，10，4，8）。 其中n为物品个数，c为背包载重量，P表示物品的价值，W表示物品的重量。请问对于此0-1背包问题，应如何选择放进去的物品，才能使到放进背包的物品总价值最大。 P=（15，8，6，4，3，1），W=（2，3，4，5，8，10），单位重量物品价值（7.5，2.67，1.5，0.8，0.375，0.1）

    正确答案： 可知随着物品的重量增加，物品的价值减少；因此可以用贪心算法来求解。以选取单位重量物品价值高为贪心策略。
    1.先把重量为2的物品放进背包，此时剩余载重量为17，P为15。
    2.把重量为3的物品放进背包，此时剩余载重量为14，P为23；
    3.把重量为4的物品放进背包，此时剩余载重量为10，P为29；
    4.把重量为5的物品放进背包，此时剩余载重量为5，P为33；
    由于8>5，所以不能再放进背包。
    结果是把重量为2，3，4，5的物品装进背包，总价值最大为33。
    解析： 暂无解析

  • 第12题：

    问答题
    对于如下描述的背包问题，请计算最终装入背包的最大价值和以及各个物品装入背包的数量。 背包容量：C＝50千克。3件物品。物品1重20千克，价值100元；物品2重20千克，价值120元；物品3重30千克，价值90元。

    正确答案： 物品1的单位重量价值为50元/千克；物品2的单位重量价值为60元/千克；物品3的单位重量价值为30元/千克。采用贪心算法解此背包问题。
    此时，贪心的策略是：每次选择单位重量价值最大的物品。因此，首先选择物品2，然后是物品1，最后是物品3，直至将背包装满。
    物品2全部装入背包，当前背包中价值120元，背包占用20千克，剩余30千克；
    物品1全部装入背包，当前背包中价值220元（120元＋100元），背包占用40千克，剩余10千克；
    物品3的1/3被装入背包，当前背包中价值250元（120元＋100元＋90元×1/3），背包占用50千克（装满）。
    因此，最终装入背包的最大价值为250元，物品1和物品2都全部装入，分别是20千克和20千克，物品3装入1/3，是10千克。
    解析： 暂无解析

  • 第13题：

    设无向图G=(P，L)，P={v1，v2，v3，v4，v5，v6}，L={(v1，v2)，(v2，v2)，(v2，v4)，(v4，v5)，(v3，v4)，(v1，v3)，(v3，v1)}。G中奇数度顶点的个数是(60)。

    A．2

    B．3

    C．4

    D．5


    正确答案：C
    解析：C中各点的度如下：dG(v1)=3，dG(v2)=4，dG(v3)=3，dG(v4)=3，dG(v5)=1，dG(v6)=0。奇数度顶点的个数为4。

  • 第14题：

    设图(a)、(b)、(c)三个质量弹簧系统的固有频率分别为w1、w2、w3，则它们之间的关系是( )。



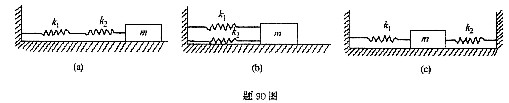
    A．w1＜w2=w3
    B．w2＜w3=w1
    C．w3＜w1=w2
    D．w1=w2=w3


    答案：A
    解析：
    求等效的弹簧系数，按串联、并联的公式计算是

  • 第15题：



    下列关于2001～2006年我国上市公司数目、上市股票数目，A股上市股票数目、B股上市股票数目年平均增长速度（顺次记为V1、V2、V3、V4）的比较正确的是（ ）。


    A. V1＞V2，V3＞V4
    B. V1＞V2，V3＜V4
    C. V1＜V2，V3＞V4
    D. V1＜V2，V3＜V4

    答案：A
    解析：
    2001～2006年上市公司数目增长（1434－1088）/1088≈31.8%，上市股票数目增长（1520－1174）/1174≈29.5%，则上市股票数目年平均增长速度也小于上市公司增长速度，即V2＜V1；从表中可以知道，B股上市股票数目基本没有增加，故V4＜V3。故答案为A。

  • 第16题：

    物资编码中首位“1、2、3”分别代表的含义是什么（）

    • A、W1：备件
    • B、W2：材料
    • C、W3：设备

    正确答案:A,B,C

  • 第17题：

    考虑背包问题：n=6，物品重量W=（1，5，2，3，6，1），价值P=（15，59，21，30，60，5），背包载重量C＝10。能放进背包的物品价值最大为（）。

    • A、101
    • B、110
    • C、115
    • D、120

    正确答案:B

  • 第18题：

    定子是电动机静止不动的部分。定子绕线有三相，其首端分别用U1、V1、W1表示，末端用U2、V2、W2表示。


    正确答案:正确

  • 第19题：

    有这样一类特殊0-1背包问题：可选物品重量越轻的物品价值越高。 n=6，c=20，P=（4，8，15，1，6，3），W=（5，3，2，10，4，8）。 其中n为物品个数，c为背包载重量，P表示物品的价值，W表示物品的重量。请问对于此0-1背包问题，应如何选择放进去的物品，才能使到放进背包的物品总价值最大，能获得的最大总价值多少？


    正确答案: 因为该0－1背包问题比较特殊，恰好重量越轻的物品价值越高，所以优先取重量轻的物品放进背包。最终可以把重量分别为2，3，4，5的三个物品放进背包，得到的价值和为15+8+6+4=33，为最大值。

  • 第20题：

    最早采用制导技术的武器是（）

    • A、美国的V1、V2导弹
    • B、美国的W1、W2导弹
    • C、德国的的V1、V2导弹
    • D、德国的的W1、W2导弹

    正确答案:C

  • 第21题：

    三相双速异步电动机高速运转时，定子绕组出线端的连接方式应为（）。

    • A、U1、V1、W1接三相电源，U2、V2、W2空着不接
    • B、U2、V2、W2接三相电源，U1、V1、W1空着不接
    • C、U1、V1、W2接三相电源，U2、V2、W1并接在一起
    • D、U2、V2、W2接三相电源，U1、V1、W1并接在一起

    正确答案:D

  • 第22题：

    单选题
    三相绕组的相带应按（）的分布规律排列。
    A

    U1—W2—V1—U2—W1—V2

    B

    U1—V1—W1—U2—V2—W2

    C

    U1—U2—V1—V2—W1—W2

    D

    U1—W1—V1—U2—W2—V2


    正确答案： A
    解析： 暂无解析

  • 第23题：

    问答题
    有这样一类特殊0-1背包问题：可选物品重量越轻的物品价值越高。 n=6，c=20，P=（4，8，15，1，6，3），W=（5，3，2，10，4，8）。 其中n为物品个数，c为背包载重量，P表示物品的价值，W表示物品的重量。请问对于此0-1背包问题，应如何选择放进去的物品，才能使到放进背包的物品总价值最大，能获得的最大总价值多少？

    正确答案： 因为该0－1背包问题比较特殊，恰好重量越轻的物品价值越高，所以优先取重量轻的物品放进背包。最终可以把重量分别为2，3，4，5的三个物品放进背包，得到的价值和为15+8+6+4=33，为最大值。
    解析： 暂无解析

  • 第24题：

    问答题
    设试验E有4个基本事件，即s＝{w1，w2，w3，w4}，并且它们发生是等可能的，又设A1＝{w1，w2}，A2＝{w1，w3}，A3＝{w1，w4}，证明：A1，A2，A3两两独立，但不相互独立。

    正确答案：
    因为A1A2={w1,w2}∩{w1,w3}={w1},P(A1A2)=1/4,P{A1}=2/4=1/2,P{A2}=2/4=1/2,P(A1)P(A2)=1/4,所以P(A1A2)=P(A1)P(A2),即A1与A2相互独立。
    同理,A1与A3相互独立,A2与A3相互独立。
    又A1A2A3={w1,w2}∩{w1,w3}∩{w1,w4}={w1},P(A1A2A3)=1/4,P(A1)P(A2)P(A3)=(1/2)×(1/2)×(1/2)=1/8,所以P(A1A2A3)≠P(A1)P(A2)P(A3),所以A1,A2,A3两两独立,但不相互独立。
    解析： 暂无解析

相关内容