32、矩阵乘法满足结合律,所以计算矩阵连乘,不同的计算次序计算量相同。
题目
32、矩阵乘法满足结合律,所以计算矩阵连乘,不同的计算次序计算量相同。
相似考题
参考答案和解析
更多“32、矩阵乘法满足结合律,所以计算矩阵连乘,不同的计算次序计算量相同。”相关问题
-
第1题:
已知一个无向图的邻接矩阵表示,计算第i个顶点的度的方法是______。A、计算邻接矩阵中第i行的元素之和
B、计算邻接矩阵中第i列的元素之和
C、计算邻接矩阵中第i行的非零元个数
D、计算邻接矩阵中第i列的非零元个数
参考答案:ABCD
-
第2题:
试题四(15分)
阅读下列说明和C代码,回答问题1至问题3,将解答写在答题纸的对应栏内。
【说明】
某工程计算中要完成多个矩阵相乘(链乘)的计算任务。
两个矩阵相乘要求第一个矩阵的列数等于第二个矩阵的行数,计算量主要由进行乘法运算的次数决定。采用标准的矩阵相乘算法,计算Am*n*Bn*p,需要m*n*p次乘法运算。
矩阵相乘满足结合律,多个矩阵相乘,不同的计算顺序会产生不同的计算量。以矩阵A110*100,A2100*5,A35*50三个矩阵相乘为例,若按(A1*A2)*A3计算,则需要进行10*100*5+10*5*50=7500次乘法运算;若按A1*(A2*A3)计算,则需要进行100*5*50+10*100*50=75000次乘法运算。可见不同的计算顺序对计算量有很大的影响。
矩阵链乘问题可描述为:给定n个矩阵<A1,A2,….An>,矩阵Ai的维数为pi-1*Pi,其中i = 1,2,….n。确定一种乘法顺序,使得这n个矩阵相乘时进行乘法的运算次数最少。
由于可能的计算顺序数量非常庞大,对较大的n,用蛮力法确定计算顺序是不实际的。经过对问题进行分析,发现矩阵链乘问题具有最优子结构,即若A1*A2*…*An的一个最优计算顺序从第k个矩阵处断开,即分为A1*A2*….Ak和Ak+1*Ak+2*…*An两个子问题,则该最优解应该包含A1*A2*…*Ak的一个最优计算顺序和Ak+1*Ak+2*…An的一个最优计算顺序。据此构造递归式,

其中,cost[i][j]表示Ai+1*Ai+2*...Aj+1的最优计算的计算代价。最终需要求解cost[0][n-1]。
【C代码】
算法实现采用自底向上的计算过程。首先计算两个矩阵相乘的计算量,然后依次计算3个矩阵、4个矩阵、…、n个矩阵相乘的最小计算量及最优计算顺序。下面是算法的C语言实现。
(1)主要变量说明
n:矩阵数
seq[]:矩阵维数序列
cost[][]:二维数组,长度为n*n,其中元素cost[i][j]表示Ai+1*Ai+2*…Aj+1的最优计算的计算代价
trace[][]:二维数组,长度为n*n,其中元素trace[i][j]表示Ai+1*Ai+2*Aj+1的最优计算对应的划分位置,即k
(2)函数cmm
define N 100
intcost[N][N];
inttrace[N][N];
int cmm(int n,int seq[]){
int tempCost;
int tempTrace;
int i,j,k,p;
int temp;
for( i=0;i<n;i++){ cost[i][i] =0;}
for(p=1;p<n;p++){
for(i=0; (1) ;i++){
(2);
tempCost = -1;
for(k = i;k<j;k++){
temp = (3) ;
if(tempCost==-1||tempCost>temp){
tempCost = temp;
(4) ;
}
}
cost[i][j] = tempCost;
trace[i][j] = tempTrace;
}
}
return cost[0][n-1];
}
【问题1】(8分)
根据以上说明和C代码,填充C代码中的空(1)~(4)。
【问题2】(4分)
根据以上说明和C代码,该问题采用了 (5) 算法设计策略,时间复杂度 (6) 。(用O符号表示)
【问题3】(3分)
考虑实例n=6,各个矩阵的维数:A1为5*10,A2为10*3,A3为3*12,A4为12*5,A5为5*50,A6为50*6,即维数序列为5,10,3,12,5,50,6。则根据上述C代码得到的一个最优计算顺序为 (7) (用加括号方式表示计算顺序),所需要的乘法运算次数为 (8) 。
正确答案:试题四分析
在解答本题时,需要注意的第一个问题便是矩阵的乘法到底是怎么进行的。
一个n行m列的矩阵可以乘以一个m行p列的矩阵,得到的结果是一个n行p列的矩阵,其中的第i行第j列位置上的数等于前一个矩阵第i行上的m个数与后一个矩阵第j列上的m个数对应相乘后所有m个乘积的和。如:
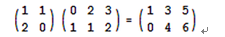
在本题中,题干部分提到“发现矩阵链乘问题具有最优子结构”,这是利用动态规划法求解最优解问题的典型特征。所以(5)应填动态规划法。
接下来分析(1)-(4)空,这几个空中,最容易回答的是(3)和(4)。(3)空可通过题目给出的递归式分析得到,其中cost数组部分与公式完全一致,而p数组在程序中是seq,所以回答时修正即可,(3)填:cost[i][k]+cost[k+1][j]+seq[i]*seq[k+1]*seq[j+1]。第(4)空的上一句为:tempCost = temp,即保存当前状态最优解,由于在保存最优解时,不仅涉及cost的记录,还涉及其位置k的记录,所以需要在此进行tempTrace=k的操作。
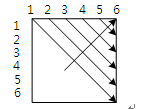
(1)与(2)相对复杂,其中(1)是对i值范围的确定,而(2)是对j的赋值操作(由于后面用到了j,但程序中没有对j的赋值,从而断定该空是对j的赋值)。两者一并起到一个效果,对cost数组操作时的操作范围与顺序。由于在进行矩阵链乘操作时,分析解空间所用到的是cost右上角的三角矩阵,而操作时,是对这个三角矩阵从左至右,呈斜线的访问(如图所示)。所以(1)和(2)分别填i<n-p和j=i+p。
该程序由于涉及3重循环,所以时间复杂度为:O(n3)。通过手动运行程序的方式可知最优解为:
(A1A2)((A3A4)(A5A6))。
总计算次数为2010。
参考答案
【问题1】
(1)i<n-p
(2)j=i+p
(3)cost[i][k]+cost[k+1][j]+seq[i]*seq[k+1]*seq[j+1]
(4)tempTrace=k
【问题2】
(5)动态规划法 (6)O(n3)
【问题3】
(7)(A1A2)((A3A4)(A5A6)) (8)2010
-
第3题:
计算25×84=25×(80+4)=25×80+25×4=2100,运用的运算律是( )。A.加法结合律
B.乘法交换律
C.乘法结合律
D.乘法分配律答案:D解析:两个数的和同一个数相乘,等于把两个加数分别同这个数相乘再把两个积加起来,结果不变,即a×(b+c)=a×b+a×c,此题运用的运算律为乘法分配律。 -
第4题:
阅读下列说明和C代码,回答问题1至问题3
【说明】 某工程计算中要完成多个矩阵相乘(链乘)的计算任务。 两个矩阵相乘要求第一个矩阵的列数等于第二个矩阵的行数,计算量主要由进行乘法运算的次数决定。采用标准的矩阵相乘算法,计算Am×n*Bn×p,需要m*n*p次乘法运算。 矩阵相乘满足结合律,多个矩阵相乘,不同的计算顺序会产生不同的计算量。以矩阵A110×100,A2100×5,A35×50三个矩阵相乘为例,若按(A1*A2)*A3计算,则需要进行10*100*5+10*5*50=7500次乘法运算;若按A1*(A2*A3)计算,则需要进行100*5*50+10*100*50=75000次乘法运算。可见不同的计算顺序对计算量有很大的影响。 矩阵链乘问题可描述为:给定n个矩阵答案:解析:
-
第5题:
已知阳阵 Am*n和 Bn*p 相乘的时间复杂度为 O(mnp)矩阵相乘满足结合律,如三个矩阵A、B、C 相乘的顺序可以是(A*B)*C),也可以是A*(B*C).不同的相乘序所需进行的乘法次数可能有很大的差别,因此确定n 个矩阵相乘的最优计算顺序是一个非常重要的问题。已知确定n 个短阵 A,A2........An 相乘的计算顺序具有最优子结构,即 A1A2..........An 的最优计算顺序包含其子问题A1A2.......Ak和 Ak+1Ak+2.......An(<=kcn)的最优计算顺序。
可以列出其递归式为
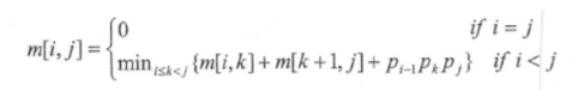
其中,A 的维度为 pi-1*pi,m【i,j】,表示 AiAi+1…A j最优计算顺字的相乘次数,
先釆用自底向上的方法求n 个矩阵相乘的最优计算顺序。则该问题的算法设计策略为(请作答此空),算法的时间复杂度为( ),空间复杂度为( )
给定一个实例,(P0Pi........P5)=(20.15.4.10.20.25)最优计算顺序为( )A.分治法
B.动态规划法
C.贪心法
D.回溯法答案:B解析:题干提到该问题具有最优子结构,并且由m[i,j]表示 AiAi+1…A j最优计算顺字的相乘次数,因此可判断该算法为动态规划法。 -
第6题:
已知矩阵 Am*n和 Bn*p 相乘的时间复杂度为 O(mnp)矩阵相乘满足结合律,如三个矩阵A、B、C 相乘的顺序可以是(A*B)*C),也可以是A*(B*C).不同的相乘序所需进行的乘法次数可能有很大的差别,因此确定n 个矩阵相乘的最优计算顺序是一个非常重要的问题。已知确定n 个短阵 A,A2........An 相乘的计算顺序具有最优子结构,即 A1A2..........An 的最优计算顺序包含其子问题A1A2.......Ak和 Ak+1Ak+2.......An(<=kcn)的最优计算顺序。
可以列出其递归式为

其中,A 的维度为 pi-1*pim【i,j】,表示 AiAi+1…A j最优计算顺字的相乘次数,
先釆用自底向上的方法求n 个矩阵相乘的最优计算顺序。则该问题的算法设计策略为( ),算法的时间复杂度为( ),空间复杂度为( )
给定一个实例,(POPi........P5)=(20.15.4.10.20.25)最优计算顺序为(请作答此空)A.(((A1*A2)*A3)*A4)*A5
B.A1*(A2*(A3*(A4*A5)))
C.((A1*A2)*A3)*(A4*A5)
D.(A1*A2)*((A3*A4)*A5)答案:D解析:矩阵链乘法: 一个给定的矩阵序列A1A2...An计算连乘乘积,有不同的结合方法,并且在结合时,矩阵的相对位置不能改变,只能相邻结合。根据矩阵乘法的公式,10*100和100*5的矩阵相乘需要做10*100*5次标量乘法。那么对于维数分别为10*100、100*5、5*50的矩阵A、B、C,用(A*B)*C来计算需要10*100*5 + 10*5*50 =7500次标量乘法;而A*(B*C)则需要100*5*50+10*100*50=75000次标量乘法。根据题干有A1-A5五个矩阵,分别为:20*15、15*4、4*10、10*20、20*25,分别带入65题各个选项,得到选项D是计算次数最少的选项。具体计算结果为:选项A:A1*A2=20*15*4=1200,(A1*A2)*A3)=20*4*10=800,(((A1*A2)*A3)*A4)=20*10*20=4000,(((A1*A2)*A3)*A4)*A5=20*20*25=10000,总的计算次数为1200+800+4000+10000=16000次。选项B:A4*A5=10*20*25=5000,A3*(A4*A5)=4*10*25=1000,A2*(A3*(A4*A5))=15*4*25=1500,A1*(A2*(A3*(A4*A5)))=20*15*25=7500,总的计算次数为:5000+1000+1500+7500=15000次。选项C:A1*A2=20*15*4=1200,(A1*A2)*A3)=20*4*10=800,A4*A5=10*20*25=5000,((A1*A2)*A3)*(A4*A5)=20*10*25=5000,总的计算次数为1200+800+5000+5000=12000次。选项D:A1*A2=20*15*4=1200,A3*A4=4*10*20=800,(A3*A4)*A5=4*20*25=2000,(A1*A2)*((A3*A4)*A5)=20*4*25=2000,总的计算次数为1200+800+2000+2000=6000次。该算法的,pi 1,pk,pj的值需要三重循环解决,因此时间复杂度为O(n^3),空间复杂度为O(n^2)。 -
第7题:
矩阵的乘法规则不满足传统的乘法交换律。
正确答案:正确 -
第8题:
定额中遇有两个或两个以上系数时,按()计算。
- A、乘法
- B、连乘法
- C、加法
- D、连加法
正确答案:B -
第9题:
创建一个4阶魔术矩阵A与单位矩阵B,并分别计算两矩阵之和、矩阵相乘、矩阵点乘、A矩阵乘方、A矩阵装置。
正确答案: >>A=magic(4)
>>B=eye(4)
>>C=A+B
>>D=A*B
>>E=A.*B
>>F=A^2
>>G=A’ -
第10题:
能用乘法结合律计算的式子是()。
- A、0.18³3+0.82³3
- B、16.5+23.5+4.9+1.1
- C、0.125³72³8
正确答案:B -
第11题:
矩阵乘法不满交换律也不满足结合律。
正确答案:错误 -
第12题:
判断题矩阵乘法不满交换律也不满足结合律。A对
B错
正确答案: 错解析: 暂无解析 -
第13题:
关于CT机矩阵的叙述,不正确的是
A.相同扫描野中矩阵越大,计算机工作量越大
B.相同扫描野中矩阵越大,图像分辨率越高
C.相同采样野矩阵越大有效野越大
D.是纵横二维排列的单位容积和像素
E.也是衰减系数的矩阵
正确答案:C
-
第14题:
两个矩阵Am*n和Bn*p相乘,用基本的方法进行,则需要的乘法次数为m*n*p 多个矩阵相乘满足结合律,不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi,M{i+i),…,Mj多个矩阵连乘的最优顺序,即所需要的乘法次数最少。最少乘法次数用m[i,j]表示,其递归式定义为:
 其中i、j和k为矩阵下标,矩阵序列中Mi的维度为(Pi-i.)*Pi采用自底向上的方法:实现该算法来确定n个矩阵相乘的顺序,其时间复杂度为( 64 )。若四个矩阵M1. M2、M3.,M4相乘的维度序列为2、6、3、10.3,采用上述算法求解,则乘法次数为( 65 )。
其中i、j和k为矩阵下标,矩阵序列中Mi的维度为(Pi-i.)*Pi采用自底向上的方法:实现该算法来确定n个矩阵相乘的顺序,其时间复杂度为( 64 )。若四个矩阵M1. M2、M3.,M4相乘的维度序列为2、6、3、10.3,采用上述算法求解,则乘法次数为( 65 )。A.O(N2)
B.O(N2Lgn)
C.O(N3)
D.O(n3lgn)
正确答案:C
-
第15题:
已知矩阵 Am*n和 Bn*p 相乘的时间复杂度为 O(mnp)矩阵相乘满足结合律,如三个矩阵A、B、C 相乘的顺序可以是(A*B)*C),也可以是A*(B*C).不同的相乘序所需进行的乘法次数可能有很大的差别,因此确定n 个矩阵相乘的最优计算顺序是一个非常重要的问题。已知确定n 个短阵 A,A2........An 相乘的计算顺序具有最优子结构,即 A1A2..........An 的最优计算顺序包含其子问题A1A2.......Ak和 Ak+1Ak+2.......An(<=kcn)的最优计算顺序。
可以列出其递归式为
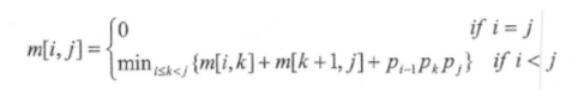
其中,A 的维度为 pi-1*pim【i,j】,表示 AiAi+1…A j最优计算顺字的相乘次数,
先釆用自底向上的方法求n 个矩阵相乘的最优计算顺序。则该问题的算法设计策略为( ),算法的时间复杂度为( ),空间复杂度为(请作答此空)
给定一个实例,(POPi........P5)=(20.15.4.10.20.25)最优计算顺序为( )A.O(n^2)
B.O(n*2lgn)
C.O(n^3)
D.O(2n)答案:A解析:矩阵链乘法: 一个给定的矩阵序列A1A2...An计算连乘乘积,有不同的结合方法,并且在结合时,矩阵的相对位置不能改变,只能相邻结合。根据矩阵乘法的公式,10*100和100*5的矩阵相乘需要做10*100*5次标量乘法。那么对于维数分别为10*100、100*5、5*50的矩阵A、B、C,用(A*B)*C来计算需要10*100*5 + 10*5*50 =7500次标量乘法;而A*(B*C)则需要100*5*50+10*100*50=75000次标量乘法。根据题干有A1-A5五个矩阵,分别为:20*15、15*4、4*10、10*20、20*25,分别带入65题各个选项,得到选项D是计算次数最少的选项。具体计算结果为:选项A:A1*A2=20*15*4=1200,(A1*A2)*A3)=20*4*10=800,(((A1*A2)*A3)*A4)=20*10*20=4000,(((A1*A2)*A3)*A4)*A5=20*20*25=10000,总的计算次数为1200+800+4000+10000=16000次。选项B:A4*A5=10*20*25=5000,A3*(A4*A5)=4*10*25=1000,A2*(A3*(A4*A5))=15*4*25=1500,A1*(A2*(A3*(A4*A5)))=20*15*25=7500,总的计算次数为:5000+1000+1500+7500=15000次。选项C:A1*A2=20*15*4=1200,(A1*A2)*A3)=20*4*10=800,A4*A5=10*20*25=5000,((A1*A2)*A3)*(A4*A5)=20*10*25=5000,总的计算次数为1200+800+5000+5000=12000次。选项D:A1*A2=20*15*4=1200,A3*A4=4*10*20=800,(A3*A4)*A5=4*20*25=2000,(A1*A2)*((A3*A4)*A5)=20*4*25=2000,总的计算次数为1200+800+2000+2000=6000次。该算法的,pi 1pkpj的值需要三重循环解决,因此时间复杂度为O(n^3),空间复杂度为O(n^2)。 -
第16题:
两个矩阵Am*n和Bn*p相乘,用基本的方法进行,则需要的乘法次数为m*n*p。多个矩阵相乘满足结合律,不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi,M(i+1),…,Mj多个矩阵连乘的最优顺序,即所需要的乘法次数最少。最少乘法次数用m[i,j]表示,其递归式定义为:
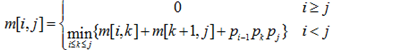
其中i、j和k为矩阵下标,矩阵序列中Mi的维度为(pi-1)*pi采用自底向上的方法实现该算法来确定n个矩阵相乘的顺序,其时间复杂度为( )A.O(n2)
B.O(n2lgn)
C.O(n3)
D.O(n3lgn)答案:C解析:四个矩阵分别为:
2*6 6*3 -
第17题:
两个矩阵Am*n和Bn*p相乘,用基本的方法进行,则需要的乘法次数为m*n*p。多个矩阵相乘满足结合律,不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi,M(i+1),…,Mj多个矩阵连乘的最优顺序,即所需要的乘法次数最少。最少乘法次数用m[i,j]表示,其递归式定义为:
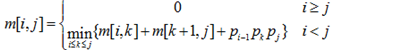
其中i、j和k为矩阵下标,矩阵序列中Mi的维度为(pi-1)*pi采用自底向上的方法实现该算法来确定n个矩阵相乘的顺序,若四个矩阵M1、M2、M3、M4相乘的维度序列为2、6、3、10、3,采用上述算法求解,则乘法次数为( )。A.156
B.144
C.180
D.360答案:B解析:四个矩阵分别为:
2*6 6*3 -
第18题:
潮流计算是以导纳矩阵为计算基础的。
正确答案:正确 -
第19题:
矩阵乘法有一个奇特的性质:不符合传统乘法的()。
- A、分配律
- B、交换律
- C、结合律
- D、消去律
正确答案:B -
第20题:
矩阵的组合特性是矩阵乘法满足结合率,不满足交换率,即进行连续变换时一定要按变换次序对变换矩阵求积后才得到总的变换矩阵。
正确答案:错误 -
第21题:
使用连乘法计算,如果结果大于1,则证明存在可套利的路径。
正确答案:正确 -
第22题:
矩阵的乘法不满足哪一规律?()
- A、结合律
- B、分配律
- C、交换律
- D、都不满足
正确答案:C -
第23题:
判断题矩阵的组合特性是矩阵乘法满足结合率,不满足交换率,即进行连续变换时一定要按变换次序对变换矩阵求积后才得到总的变换矩阵。A对
B错
正确答案: 对解析: 暂无解析 -
第24题:
单选题矩阵的乘法不满足哪一规律?()A结合律
B分配律
C交换律
D都不满足
正确答案: B解析: 暂无解析
