最短路径A.标号法求解单源点最短路径:vara:array[1..maxn,1..maxn] of integer;b:array[1..maxn] of integer; {b[i]指顶点i到源点的最短路径}mark:array[1..maxn] of boolean;procedure bhf;varbest,best_j:integer;
题目
最短路径
A.标号法求解单源点最短路径:
var
a:array[1..maxn,1..maxn] of integer;
b:array[1..maxn] of integer; {b[i]指顶点i到源点的最短路径}
mark:array[1..maxn] of boolean;
procedure bhf;
var
best,best_j:integer;
相似考题
更多“最短路径A.标号法求解单源点最短路径:vara:array[1..maxn,1..maxn] of integer;b:array[1..maxn] of integer; {b[i]指顶点i到源点的最短路径}mark:array[1..maxn] of boolean;procedure bhf;varbest,best_j:integer;”相关问题
-
第1题:
在软件开发项目中,关键路径是项目事件网络中 (66) ,组成关键路径的活动称为关键活动。下图中的关键路径历时 (67) 个时间单位。
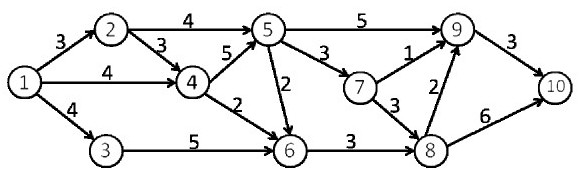
(66)
A.最长的回路
B.最短的回路
C.源点和汇点间的最长路径
D.源点和汇点间的最短路径
正确答案:C
-
第2题:
Dijkstra最短路径算法从源点到其余各顶点的最短路径的路径长度按递增次序依次产生。()此题为判断题(对,错)。
正确答案:√
-
第3题:
●迪杰斯特拉(Dijkstra)算法用于求解图上的单源点最短路径。该算法按路径长度递增次序产生最短路径,本质上说,该算法是一种基于(62)策略的算法。
(62)
A.分治
B.动态规划
C.贪心
D.回溯
正确答案:C
-
第4题:
● 迪杰斯特拉(Dijkstra)算法用于求解图上的单源点最短路径。该算法按路径长度递增次序产生最短路径,本质上说,该算法是一种基于(61)策略的算法。 A.分治 B.动态规划 C.贪心 D.回溯
正确答案:C
试题61分析分治法:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决;否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。动态规划法:这种算法也用到了分治思想,它的做法是将问题实例分解为更小的、相似的子问题,并存储子问题的解而避免计算重复的子问题。贪心算法:它是一种不追求最优解,只希望得到较为满意解的方法。贪心算法一般可以快速得到满意的解,因为它省去了为找到最优解而穷尽所有可能所必须耗费的大量时间。贪心算法常以当前情况为基础做最优选择,而不考虑各种可能的整体情况,所以贪心算法不要回溯。回溯算法(试探法):它是一种系统地搜索问题的解的方法。回溯算法的基本思想是:从一条路往前走,能进则进,不能进则退回来,换一条路再试。其实现一般要用到递归和堆栈。针对单源最短路径问题,由Dijkstra提出了一种按路径长度递增的次序产生各顶点最短路径的算法。若按长度递增的次序生成从源点s到其他顶点的最短路径,则当前正在生成的最短路径上除终点以外,其余顶点的最短路径均已生成(将源点的最短路径看做是已生成的源点到其自身的长度为0的路径)。这是一种典型的贪心策略,就是每递增一次,经对所有可能的源点、目标点的路径都要计算,得出最优。带权图的最短路径问题即求两个顶点间长度最短的路径。其中:路径长度不是指路径上边数的总和,而是指路径上各边的权值总和。参考答案(61)C -
第5题:
最小生成树
A.Prim算法:
procedure prim(v0:integer);
var
lowcost,closest:array[1..maxn] of integer;
i,j,k,min:integer;
正确答案:begin
for i:=1 to n do begin
lowcost[i]:=cost[v0,i];
closest[i]:=v0;
end;
for i:=1 to n-1 do begin
{寻找离生成树最近的未加入顶点k}
min:=maxlongint;
for j:=1 to n do
if (lowcost[j]<min) and (lowcost[j]<>0) then begin
min:=lowcost[j];
k:=j;
end;
lowcost[k]:=0; {将顶点k加入生成树}
{生成树中增加一条新的边k到closest[k]}
{修正各点的lowcost和closest值}
for j:=1 to n do
if cost[k,j]<lwocost[j] then begin
lowcost[j]:=cost[k,j];
closest[j]:=k;
end;
end;
end;{prim} -
第6题:
C. Dijkstra 算法:
var
a:array[1..maxn,1..maxn] of integer;
b,pre:array[1..maxn] of integer; {pre[i]指最短路径上I的前驱结点}
mark:array[1..maxn] of boolean;
procedure dijkstra(v0:integer);
正确答案:begin
fillchar(mark,sizeof(mark),false);
for i:=1 to n do begin
d[i]:=a[v0,i];
if d[i]<>0 then pre[i]:=v0 else pre[i]:=0;
end;
mark[v0]:=true;
repeat {每循环一次加入一个离1集合最近的结点并调整其他结点的参数}
min:=maxint; u:=0; {u记录离1集合最近的结点}
for i:=1 to n do
if (not mark[i]) and (d[i]<min) then begin
u:=i; min:=d[i];
end;
if u<>0 then begin
mark[u]:=true;
for i:=1 to n do
if (not mark[i]) and (a[u,i]+d[u]<d[i]) then begin
d[i]:=a[u,i]+d[u];
pre[i]:=u;
end;
end;
until u=0;
end; -
第7题:
第n最短路径问题
*第二最短路径:每举最短路径上的每条边,每次删除一条,然后求新图的最短路径,取这些路径中最短的一条即为第二最短路径。
*同理,第n最短路径可在求解第n-1最短路径的基础上求解。
正确答案: -
第8题:
关键路径是指AOE(Activity On Edge)网中______。
A.最长的回路
B.最短的回路
C.从源点到汇点(结束顶点)的最长路径
D.从源点到汇点(结束顶点)的最短路径
正确答案:C
-
第9题:
在软件开发项目中,关键路径是项目事件网络中 (66) ,组成关键路径的活动称为关键活动A. 最长的回路
B. 最短的回路
C. 源点和汇点间的最长路径
D. 源点和汇点间的最短路径答案:C解析: -
第10题:
从源点到终点的最短路径是唯一的。
正确答案:错误 -
第11题:
关键路径是AOE网中()。
- A、从源点到终点的最长路径
- B、从源点到终点的最短路径
- C、最长的回路
- D、最短的回路
正确答案:B -
第12题:
单选题关键路径是事件结点网络中( )。A从源点到汇点的最长路径
B从源点到汇点的最短路径
C最长回路
D最短回路
正确答案: A解析: -
第13题:
在AOE图中,关键路径是(39)。
A.从源点到汇点的最长路径
B.从源点到汇点的最短路径
C.最长的回路
D.最短的回路
正确答案:A
解析:在带权有向图G中以顶点表示事件,以有向边表示活动,边上的权值表示该活动持续的时间,则这种带权有向图称为用边表示活动的网,简称AOE图。用AOE图表示一项工程计划时,对于一项工程来说,一般有一个开始状态和一个结束状态,所以在AOE网中至少有一个入度为0的开始顶点,称其为源点;另外,应有一个出度为。的结束顶点,称其为汇点。AOE中不应存在有向回路,否则整个工程无法完成。从源点到汇点的路径中,长度最长的路径称为关键路径,所以应选A。 -
第14题:
关键路径是指AOE(Active On Edge)网中______。
A.最长的回路
B.最短的回路
C.从源点到汇点(结束顶点)的最长路径
D.从源点到汇点(结束顶点)的最短路径
A.
B.
C.
D.
正确答案:C
解析:AOE(Activity On Edge)网是一个有向图,通常用来估算工程的完成时间,图中的顶点表示事件,有向边表示活动,边上的权表示完成这一活动所需的时间。AOE网没有有向回路,存在唯一的入度为O的开始顶点,及唯一的出度为O的结束顶点。对AOE网最关心的两个问题是:完成整个工程至少需要多少时间?哪些活动是影响工程进度的关键?这就引出两个概念:关键路径和关键活动。
· 关键路径:从开始顶点到结束顶点的最长路径,路径的长度也是工程完成的最少时间。
· 关键活动:关键路径上的所有活动,关键活动的最大特征是:该活动的最早开始时间等于该活动所允许的最迟开始时间。关键活动拖延时间,整个工程也要拖延时间。求关键路径只需求出起点到终点的最长路径。注意,关键路径不是唯一的。 -
第15题:
关键路径是事件结点网络中()。
A.从源点到汇点的最长路径
B.从源点到汇点的最短路径
C.最长回路
D.最短回路
正确答案:A
-
第16题:
关键路径是指AOE(Activity On Edge)网中(38)。
A.最长的回路
B.最短的回路
C.从源点到汇点(结束顶点)的最长路径
D.从源点到汇点(结束顶点)的最短路径
正确答案:C
解析:在AOE网中,用顶点表示活动,用有向边vi,vi>表示活动vi必须先于活动vi进行。如果在有向环的带权有向图中用有向边表示一个工程中的各项活动,用有向边上的权值表示活动的持续时间,用顶点表示事件,则这种有向图叫做用边表示活动的网络,简称AOE网络。关键路径是指在AOE网络中从源点到汇点的最长路径。拓扑排序、最短路径和计算关键路径都是有向图的重要运算。根据关键路径的定义,正确答案为C。 -
第17题:
B.Floyed算法求解所有顶点对之间的最短路径:
procedure floyed;
正确答案:begin
for I:=1 to n do
for j:=1 to n do
if a[I,j]>0 then p[I,j]:=I else p[I,j]:=0; {p[I,j]表示I到j的最短路径上j的前驱结点}
for k:=1 to n do {枚举中间结点}
for i:=1 to n do
for j:=1 to n do
if a[i,k]+a[j,k]<a[i,j] then begin
a[i,j]:=a[i,k]+a[k,j];
p[I,j]:=p[k,j];
end;
end; -
第18题:
计算图的传递闭包
Procedure Longlink;
Var
T:array[1..maxn,1..maxn] of boolean;
正确答案:Begin
Fillchar(t,sizeof(t),false);
For k:=1 to n do
For I:=1 to n do
For j:=1 to n do T[I,j]:=t[I,j] or (t[I,k] and t[k,j]);
End; -
第19题:
高精度数的定义:
type
hp=array[1..maxlen] of integer;
1.高精度加法
procedure plus ( a,b:hp; var c:hp);
var i,len:integer;
正确答案:begin
fillchar(c,sizeof(c),0);
if a[0]>b[0] then len:=a[0] else len:=b[0];
for i:=1 to len do begin
inc(c[i],a[i]+b[i]);
if c[i]>10 then begin dec(c[i],10); inc(c[i+1]); end; {进位}
end;
if c[len+1]>0 then inc(len);
c[0]:=len;
end;{plus} -
第20题:
关键路径是AOE网中()。A.最长的回路
B.最短的回路
C.从源点到终点的最长路径
D.从源点到终点的最短路径答案:C解析:关键路径是指从开始顶点到结束顶点的最短路径,路径的长度也是工程完成的最少时间。关键活动是指关键路径上的所有活动,关键活动的最大特征是该活动的最早开始时间等于该活动所允许的最迟开始时间。 -
第21题:
在软件开发项目中,关键路径是项目事件网络中(请作答此空) ,组成关键路径的活动称为关键活动。下图中的关键路径历时( )个时间单位。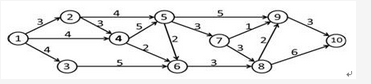 A. 最长的回路
A. 最长的回路
B. 最短的回路
C. 源点和汇点间的最长路径
D. 源点和汇点间的最短路径答案:C解析:图论中给出了关键路径的定义,即源点到汇点的最长路径为关键路径。
关键路径的识别与计算:
通过观察法可得出关键路径为1-2-4-5-7-8-10,最长路径的历时为3+3+5+3+3+6=23。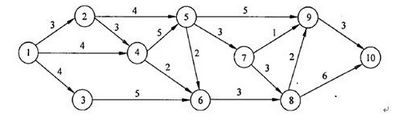
-
第22题:
关键路径是事件结点网络中()。
- A、从源点到汇点的最长路径
- B、从源点到汇点的最短路径
- C、最长的回路
- D、最短的回路
正确答案:A -
第23题:
单选题关键路径是事件结点网络中()。A从源点到汇点的最长路径
B从源点到汇点的最短路径
C最长的回路
D最短的回路
正确答案: D解析: 暂无解析
