短期生产数函数是指()A.生产函数中所有投入要素的投入量都是可变的B.生产函数中所有投入要素的投入量都是不可变的C.生产函数中有的投入要素的投入量都是可变的,有的不固定不变
题目
短期生产数函数是指()
A.生产函数中所有投入要素的投入量都是可变的
B.生产函数中所有投入要素的投入量都是不可变的
C.生产函数中有的投入要素的投入量都是可变的,有的不固定不变
相似考题
更多“短期生产数函数是指() ”相关问题
-
第1题:
企业的生产函数为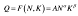
工资率为w,资本价格为r。 短期资本存量不变,求短期成本函数。答案:解析: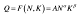
-
第2题:
有一种投入是固定不变的生产函数是短期生产函数。
正确因为,短期即指至少有一种生产要素的数量是固定不变的时间周期。 -
第3题:
12、短期平均成本曲线呈U形的原因是短期生产函数的()的作用。
短期平均成本曲线呈U形,也就是最初阶段递减后又转入递增阶段。之所以产生这种现象是由于产量达到一定数量前,每增加一单位的可变要素所增加的产量超过先前每单位可变要素之平均产量。这表明,平均每单位成本随产量的增加而递减。当产量达到一定数量后,随投入可变要素的增加,每增加一单位可变要素所增加的产量小于先前的可变要素的平均产量,即短期平均可变成本曲线由此点开始转入递增。 长期平均成本曲线呈U形的原因在于,随产量的扩大,使用的厂房设备等的规模扩大,因此产品的生产经历规模报酬递增阶段,这表现为产品的单位成本将随着产量的增加而递减。长期平均成本经历递减阶段后,最好的资本设备和专业化的利益已全被利用,此时可能进入报酬不变,即平均成本固定不变阶段,由于企业管理这个生产要素不会象其他要素那样增加,所以随着企业规模的扩大,管理的困难和成本将越来越增加,如果再增加产量,企业的长期平均成本最终将转为递增。 作为包络线的长期平均成本曲线上的每一点总是与某一特定的短期平均成本曲线相切,但长期平均成本曲线并非全是各条短期平均成本曲线的最低点构成的。事实上,长期平均成本曲线上只有一点才是某一特定的短期平均成本曲线的最低点。具体而言 ①只有长期平均成本本身的最低点T 3 与之相应的SAC 3 相切之点才是SAC 3 的最低点,T 3 点是LAC曲线的最低点,所以过T 3 作LAC曲线的切线的斜率是零。又因为SAC 3 与LAC相切于T 3 点,所以SAC 3 在T 3 点的切线的斜率也是零。因此,T 3 也是呈U形的SAC 3 的最低点。 ②当MC处于递减阶段时,即在T 3 的左边,LAC曲线各点与SAC曲线相切之点必然位于SAC曲线的最低点的左边和上边。或者说SAC曲线的最低点必然位于切点的右方和下方。LAC与SAC 2 切于T 2 点,因为T 2 点位于SAC 2 的最低点的左边,以及该产品的生产处于规模报酬递增(平均成本递减)阶段,因此LAC曲线上的T 2 点的切线的斜率为负。所以,SAC 2 曲线在T 2 点的切线的斜率也为负。所以,位于T 3 点(LAC曲线的最低点)左边的LAC上的各个点都不是有关SAC曲线的最低点。 ③当LAC曲线处于递增阶段时,也就是T 3 点的右边部分,LAC曲线各点与各SAC曲线相切之点必然位于,SAC曲线的最低点的右边和上边。或者说SAC曲线的最低点必然位于切点的左边和下面。LAC和SAC 4 切于T 4 点,因为T 4 点位于SAC 4 的最低点的右边,该产品的生产处于规模报酬递减(平均成本递增)阶段,因而LAC曲线上的T 4 点的切线的斜率为正。所以,SAC 4 曲线上的T 4 点的斜率也为正数。由此可知,T 4 不是SAC 4 的最低点。 综上所述,由无数条短期平均成本曲线推导出来的长期平均成本曲线有且只有一点与短期平均成本曲线相等。 -
第4题:
简要说明在短期中,生产函数与成本函数之间的关系答案:解析:(1)厂商的短期成本函数可以由成本、产量以及要素投入量之间的关系推导得出,因为一定的要素投入量生产一定产量的产品,同时也必然花费一定的成本。成本与产量之间的对应关系即为成本函数。即若给定生产函数为Q= f(L,K),以及成本方程为C=L·PLK·PK+ CO,根据最优要素投入量的选择原则MPL/PL= MPK/PK,就可以获得短期成本函数C=C(Q)。 (2)平均可变成本AVC与给定要素价格下的可变要素数量及产量相关,因而也就与其平均产量相关;边际成本MC与给定要素价格下的边际产量相关。即: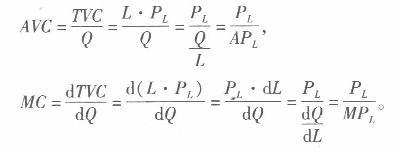
所以,APL与4VC的变化趋势相反,APL曲线呈倒U形,AVC曲线呈U形;MPL与MC的变化趋势也相反,MP。曲线呈倒U形,MC曲线则呈U形。 -
第5题:
29、在生产函数中,只要有一种投入要素不变,便是短期生产函数
正确
