“严谨性与量力性相结合”是数学教学的基本原则。 (1)简述严谨性与量力性相结合教学原则的内涵; (2)初中数学教学中“负负得正”运算法则引入的方式有哪些?请写出至少两种; (3)在初中“负负得正”运算法则的教学中,如何体现“严谨性与量力性相结合”的教学原则?

题目
“严谨性与量力性相结合”是数学教学的基本原则。
(1)简述严谨性与量力性相结合教学原则的内涵;
(2)初中数学教学中“负负得正”运算法则引入的方式有哪些?请写出至少两种;
(3)在初中“负负得正”运算法则的教学中,如何体现“严谨性与量力性相结合”的教学原则?

相似考题

1.在中学数学教学中，主要应遵循如下基本原则：A、抽象与具体相结合原则B、严谨性与量力性相结合原则C、理论与实际相结合原则D、巩固与发展相结合原则。

2.在中学数学教学中，如何贯彻严谨性与量力性相结合原则

3.数学教学中如何贯彻严谨性与量力性相结合的原则

4.通过温度的升降,货物的进出等实例引进具有相反意义的量,再进一步提出正数、负数的概念。说明了在教学中要遵循()A.严谨性与量力性相结合的原则B.理论与实际相结合的原则C.主动性与过程性相结合的原则D.具体与抽象相结合的原则

参考答案和解析
答案：
解析：
(1)数学的严谨性,是指数学具有很强的逻辑性和较高的精确性,即逻辑的严格性和结论的确定性。量力性是指学生的可接受性。这一原则,说明教学中的数学知识的逻辑严谨性与学生的可接受性之间相适应的关系。理论知识的严谨程度要适合学生的一般知识结构与智力发展水平,随着学生知识结构的不断完善,心理发展水平的提高,逐渐增强理论的严谨程度;反过来,又要通过恰当的理论严谨性逐渐促进学生的接受能力。
显然,这一原则是根据数学本身的特点及学生心理发展的特点提出的。但是,在学习过程中,学生的心理发展使逐步形成的,不同的年龄阶段,其感知、记忆、想象、思维、能力等心理因素都有不同的发展水平。这种心理发展的渐变性决定了在教学中不可能对数学理论的研究达到完全严密的程度,而应该在不同的教学阶段,依据不同的教学目的和内容而提出不同的严谨性要求。即数学教学的严谨性是相对的。
(2)测量模型:某气象站测得海拔每升高1千米,温度降低0.6度,观察地的气温是0度,问在观察地点以下3千米的地方,气温是多少度?我们规定,气温升高为正,气温下降为负,观察地点以上为正,观察地以下为负,易得出问题算式(-0.6)×(-3)=1.8。
寻找模式法:由正数与负数,负数与零相乘的法则,可以得出下列式子:
(-4)×(+3)=-12;
(-4)×(+2)=-8;
(-4)×(+1)=-4;
(-4)×(0)=0;
(-4)×(-1)=?;
(-4)×(-2)=?;
(-4)×(-3)=?;
仔细观察可以发现,从上到下,被乘数是不变的,乘数每减少1,积就增加4,因此,0增加4得到4,然后是8和12,所以(-4)×(-1)=4;
(-4)×(-2)=8;(-4)×(-3)=12;从而引出“负负得正”运算法则。
(3)在初中“负负得正”运算法则的教学中,可以根据学生的认知水平和学生接受的难易程度入手,设法安排学生逐步适应的过程与机会,从正数乘以负数积为负数入手,从上到下,被乘数是不变的,乘数每减少1,积就增加一个数4.然后再利用一些数字模型解析“负负得正”运算法则,达到严谨性与量力性相结合。
更多““严谨性与量力性相结合”是数学教学的基本原则。 ”相关问题

  • 第1题：

    叙述“严谨性与量力性相结合”数学教学原则的内涵。并以“√2是无理数”的教学过程为例，说明在教学中如何体现该教学原则。


    答案：
    解析：
    (1)数学的严谨性，是指数学具有很强的逻辑性和较高的精确性，即逻辑的严格性和结论的确定性。量力性是指学生的可接受性。
    这一原则，说明教学中的数学知识的逻辑严谨性与学生的可接受性之间相适应的关系。理论知识的严谨程度要适合学生的一般知识结构与智力发展水平，随着学生知识结构的不断完善，心理发展水平的提高，逐渐增强理论的严谨程度：反过来，又要通过恰当的理论严谨性逐渐促进学生的接受能力。
    显然．这一原则是根据数学本身的特点及学生心理发展的特点提出的。但是，在学习过程中，学生的心理发展是逐步形成的，不同的年龄阶段，其感知、记忆、想象、思维、能力等心理因素都有不同的发展水平。这种心理发展的渐变性决定了在教学中不可能对数学理论的研究达到完全严密的程度，而应该在不同的教学阶段，依据不同的教学目的和内容而提出不同的严谨性要求，即数学教学的严谨性是相对的。
    (2)在证明“根号2是无理数”的教学过程，对严谨性要求，应设法安排使学生逐步适应的过程与机会，逐步提高其严谨程度，要求做到推理有据，证明要步步有根据、处处有逻辑。在推理有据的同时并不排斥直观和猜想，强调思维的严谨性．允许猜想、辩证地处理好推理的有据和猜想的关系。
    由于学生对无理数不熟悉，在实际教学过程中我们采用反证法，先假设是有理数。教学中可以由教师给出证明步骤，让学生只填每一步的理由，鼓励学生发扬“跳一跳够得到”的精神，逐步过渡到学生自己给出严格证明，最后要求达到立论有据，论证简明。“因为如果x是有理数，那么x可以写成最简分数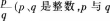 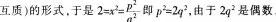所以P也是偶数。不妨设p=2a，可得 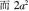是偶数，所以q应是偶数，这样P、q都是偶数了，它们的公约数是2，与P、q互质矛盾。可见，x不是有理数，而是无理数。在教学过程中，不能消极适应学生，降低理论要求，必须在符合内容科学性的前提下，结合学生实际组织教学。

  • 第2题：

    严谨性与量力性相结合”是数学教学的基本原则。

    （1）简述“严谨性与量力性相结合”教学原则的内涵（3分）；

    （2）初中数学教学中“负负得正”运算法则引入的方式有哪些？请写出至少两种（6分）；

    （3）在初中“负负得正”运算法则的教学中，如何体现“严谨性与量力性相结合”的教学原则？（6分）


    答案：
    解析：
    本题主要考查严谨性与量力性的教学原则，以及课堂导入技巧的教学技能知识。

    （1） “严谨性与量力性相结合”教学原则的内涵是指数学逻辑的严密性及结论的精确性，在中学的数学理论中也不例外。所谓数学的严谨性，就是指对数学内容结论的叙述必须精确，结论的论证必须严格、周密，整个数学内容被组织成一个严谨的逻辑系统。教材有时对有些内容避而不谈，或用直观说明，或用不完全归纳法验证，或不必说明的作了说明，或扩大公理体系等，这些做法主要是考虑到学生的可接受性，估计降低内容的严谨性，让学生更好地掌握要学的数学内容。当前数学界提出的“淡化形式，注重实质”的口号实质上也是侧面反映出数学必须坚持严谨性与量力性相结合原则的问题。

    （2）初中数学教学中“负负得正”运算法则引入的方式可以从生活中的负数入手，举出两个引入的方式即可。

    （3）在初中“负负得正”运算法则的教学中，可以根据学生的认知水平和学生接受的难易程度入手，设法安排学生逐步适应的过程与机会，然后再利用一些数学模型解析“负负得正”运算法则，从而体现“严谨性与量力性相结合”的教学原则。

  • 第3题：

    在数学教学中，我们应该遵守怎么样的原创：（） 1.抽象与具体远侧；2.严谨性与量力性原则；3.理论与实际原则；4.巩固与发展原则

    • A、1，2，3
    • B、1，3，4
    • C、2，3，4
    • D、1.2.3.4

    正确答案:D

  • 第4题：

    "学生的发展水平是教学的出发点"反映了以下哪条教学原则（）。

    • A、量力性原则
    • B、巩固性原则
    • C、启发性原则
    • D、理论与实际相结合原则
    • E、科学性、思想性和艺术性相结合原则

    正确答案:A

  • 第5题：

    数学应用题较好地体现了（）的原则。

    • A、抽象与具体相结合
    • B、严谨性与量力性相结合
    • C、理论与实际相结合
    • D、巩固与发展相结合

    正确答案:C

  • 第6题：

    苏联心理学家维果茨基说：“教育学不应当把眼睛看着儿童发展的昨天，而应当看着儿童发展的明天。”这句话这体现了以下哪种数学教学原则：（）

    • A、抽象与具体相结合原则
    • B、严谨性与量力性相结合原则
    • C、理论与实际相结合原则
    • D、巩固与发展相结合原则

    正确答案:D

  • 第7题：

    李老师运用录像带进行口腔护理教学是遵循了以下哪条原则（）

    • A、理论与实际相结合原则
    • B、统一要求与因材施教相结合原则
    • C、量力性原则
    • D、直观性与抽象性相结合原则
    • E、系统性与循序渐进性相结合原则

    正确答案:D

  • 第8题：

    单选题
    苏联心理学家维果茨基说：“教育学不应当把眼睛看着儿童发展的昨天，而应当看着儿童发展的明天。”这句话这体现了以下哪种数学教学原则：（）
    A

    抽象与具体相结合原则

    B

    严谨性与量力性相结合原则

    C

    理论与实际相结合原则

    D

    巩固与发展相结合原则


    正确答案： B
    解析： 暂无解析

  • 第9题：

    单选题
    数学应用题较好地体现了（）的原则。
    A

    抽象与具体相结合

    B

    严谨性与量力性相结合

    C

    理论与实际相结合

    D

    巩固与发展相结合


    正确答案： C
    解析： 数学应用题较好地体现了理论联系实际的原则。

  • 第10题：

    问答题
    论述如何贯彻尽力性与量力性相结合的原则。

    正确答案： 尽力性与量力性相结合的原则，是指教学中所选择的内容、提出的要求，是学生付出较大努力才能掌握的，同时又不能超越他们学习的能力。这一原则是由学生身心发展规律所决定的；“最近发展区”的研究，为尽力性与量力性相结合的教学原则提供了心理学的依据。贯彻这一原则的基本要求是：
    （1）要对学生的发展水平作出科学的估计对学生身心发展水平的估计，既不能过高也不能过低，应从学生实际出发。
    （2）要做到“及时而教”教师要随着学生知识的增长，能力的提高，及时提出新的更高的要求，及时更改教学内容和方法。
    （3）要努力改进教学方法教学中的难与易是可以相互转化的。这种转化的条件，在很大程度上取决于教师的教学方法。
    解析： 暂无解析

  • 第11题：

    单选题
    "学生的发展水平是教学的出发点"反映了以下哪条教学原则（）。
    A

    量力性原则

    B

    巩固性原则

    C

    启发性原则

    D

    理论与实际相结合原则

    E

    科学性、思想性和艺术性相结合原则


    正确答案： C
    解析： 暂无解析

  • 第12题：

    问答题
    如何理解和贯彻数学教学中的严谨性与量力性相结合的教学原则？

    正确答案：
    (1)数学理论的严谨性
    严谨性是数学科学理论的基本特点,它要求数学结论的表述必须精练、准确;而对结论的推理论证则要求步步有根据,处处符合逻辑理论的要求;在数学内容的安排上,要求有严格的系统性,要符合学科内在的逻辑结构,既严格又周密。数学科学的严谨性是相对的,逐步提高的。
    (2)中学生的可接受性(量力性)
    对数学严谨性的要求,根据中学生的年龄特征和认知发展水平,只能逐步适应;对数学严谨性的认识具有相对性;智力发展的可塑性很大,应该积极诱导,促进思维发展,充分发挥学生的潜能。
    (3)严谨性与量力性相结合
    首先,必须注意到数学理论的严谨性具有相对性,在它达到当前高度严谨以前,也有一个相对来说不那么严谨的过程;对于数学严谨性的要求,中学生要有一个适应过程,严谨性的程度应是学生能够接受的教学安排,要有一定的梯度,要选择最便于学生接受的方式处理教学内容,教学安排上要有适当的梯度。
    其次,可以通过下列要求来贯彻这一个教学原则:教师必须明确各部分内容在严谨性上的要求程度;要求学生语言精确;要求学生思考缜密;要求学生言必有据;要求学生思路清晰。
    解析： 暂无解析

  • 第13题：

    叙述“严谨性与量力性相结合”数学教学原则的内涵,并以“是无理数”的教学过程为例,说明在教学中如何体现该教学原则。


    答案：
    解析：
    (1)数学的严谨性，是指数学具有很强的逻辑性和较高的精确性,即逻辑的严格性和结论的确定性。量力性是指学生的可接受性。
    这一原则，说明教学中的数学知识的逻辑严谨性与学生的可接受性之间相适应的关系。理论知识的严谨程度要适合学生的一般知识结构与智力发展水平，随者学生知识结构的不断完善，心理发展水平的提高，逐渐增强理论的严谨程度;反过来，又要通过恰当的理论严谨性逐渐促进学生的接受能力。
    显然,这一原则是根据数学本身的特点及学生心理发展的特点提出的。但是,在学习过程中，学生的心理发展是逐步形成的,不同的年龄阶段,其感知、记忆、想象、思维、能力等心理因素都有不同的发展水平。这种心理发展的渐变性决定了在教学中不可能对数学理论的研究达到完全严密的程度，而应该在不同的教学阶段，依据不同的教学目的和内容而提出不同的严谨性要求,即数学教学的严谨性是相对的。

  • 第14题：

    “严谨性与量力性相结合”是数学教学的基本原则。

    （1）简述“严谨性与量力性相结合”教学原则的内涵（3分）；

    （2）实数指数幂在数学上如何引入的？（6分）

    （3）在高中“实数指数幂”概念的教学中，如何体现“严谨性与量力性相结合”的教学原则。（6分）


    答案：
    解析：
    本题主要考查严谨性与量力性的教学原则，以及课堂导入技巧的教学技能知识。

    （1） “严谨性与量力性相结合”教学原则的内涵是指数学逻辑的严密性及结论的精确性，在中学的数学理论中也不例外。所谓数学的严谨性，就是指对数学内容结论的叙述必须精确，结论的论证必须严格、周密，整个数学内容被组织成一个严谨的逻辑系统。教材有时对有些内容避而不谈，或用直观说明，或用不完全归纳法验证，或不必说明的作了说明，或扩大公理体系等，这些做法主要是考虑到学生的可接受性，估计降低内容的严谨性，让学生更好地掌握要学的数学内容。当前数学界提出的“淡化形式，注重实质”的口号实质上也是侧面反映出数学必须坚持严谨性与量力性相结合原则的问题。

    （2）对于实数指数幂在教学上，首先可以从初中学习的整数指数幂的概念和运算性质出发，比如回顾平方根和立方根的基础上，类比出正数的n次方根的定义，从而把指数推广到分数指数，进而推广到有理数指数，在推广到实数指数，并将幂的运算性质由整数指数幂推广到实数指数幂。

    （3）在高中“实数指数幂”的概念教学中，对严谨性要求，设法安排学生逐步适应的过程与机会，逐步提高其严谨程度，做到立论有据。比如学生初学分数指数幂很不适应，教师可以引导学生研究已学习过整数指数幂的概念属性，理解分数指数幂的概念，进而学习指数幂的性质，并学习分数指数幂和根式之间的互化，渗透“转化”的数学思想，最后达到知识点之间的密切联系，达到概念的产生有根有据。

  • 第15题：

    根据护理教学需要，组织好各种复习，是遵循了以下哪条教学原则（）

    • A、量力性原则
    • B、巩固性原则
    • C、启发性原则
    • D、理论与实际相结合原则
    • E、科学性、思想性和艺术性相结合原则

    正确答案:B

  • 第16题：

    下列哪项不属于护理教学原则（）

    • A、理论与实践相结合的原则
    • B、专业性和综合性相结合的原则
    • C、创造性原则
    • D、启发性原则
    • E、量力性原则

    正确答案:C

  • 第17题：

    数学教学原则包括（） 一抽象与具体相结合原则； 二严谨性与量力性相结合原则； 三理论与实际相结合原则； 四巩固与发展相结合原则。

    • A、一二三
    • B、一二四
    • C、一三四
    • D、一二三四

    正确答案:D

  • 第18题：

    下列不属于选择小学数学课程内容的基本原则的是（）

    • A、基础性原则
    • B、学术性原则
    • C、可接受性与发展性相结合原则
    • D、统一性与灵活性相结合的原则

    正确答案:B

  • 第19题：

    “读万卷书，行万里路”体现的是（）教学原则。

    • A、科学性与教育性相结合
    • B、理论联系实际
    • C、启发性
    • D、量力性

    正确答案:B

  • 第20题：

    单选题
    下列不属于选择小学数学课程内容的基本原则的是（）
    A

    基础性原则

    B

    学术性原则

    C

    可接受性与发展性相结合原则

    D

    统一性与灵活性相结合的原则


    正确答案： D
    解析： 暂无解析

  • 第21题：

    单选题
    根据护理教学需要，组织好各种复习，是遵循了以下哪条教学原则（）
    A

    量力性原则

    B

    巩固性原则

    C

    启发性原则

    D

    理论与实际相结合原则

    E

    科学性、思想性和艺术性相结合原则


    正确答案： A
    解析： 暂无解析

  • 第22题：

    单选题
    数学教学原则包括（） 一抽象与具体相结合原则； 二严谨性与量力性相结合原则； 三理论与实际相结合原则； 四巩固与发展相结合原则。
    A

    一二三

    B

    一二四

    C

    一三四

    D

    一二三四


    正确答案： C
    解析： 暂无解析

  • 第23题：

    单选题
    李老师运用录像带进行口腔护理教学是遵循了以下哪条原则（）
    A

    理论与实际相结合原则

    B

    统一要求与因材施教相结合原则

    C

    量力性原则

    D

    直观性与抽象性相结合原则

    E

    系统性与循序渐进性相结合原则


    正确答案： D
    解析： 暂无解析

相关内容