轴对称图形和两个图形成轴对称的区别和联系是什么?【数学专业问题】

题目
轴对称图形和两个图形成轴对称的区别和联系是什么?【数学专业问题】

相似考题

1.在轴对称问题中，应力分量和位移分量一般都与极角无关。()

2.下列平面图形中,即是轴对称图形又是中心对称图形的是( )A.AB.BC.CD.D

3.设三次函数 , 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是A.关于y轴对称 B.关于原点对称 C.关于直线y=x轴对称 D.以上均错

4.位移轴对称时，其对应的应力分量一定也是轴对称的;反之，应力轴对称时，其对应的位移分量一定也是轴对称的。()

更多“轴对称图形和两个图形成轴对称的区别和联系是什么?【数学专业问题】”相关问题

  • 第1题：

    学生在学习正方形、长方形、三角形时已形成了轴对称图形概念，在学习圆时，学生立即就能发现圆具有轴对称图形的一切特征，从而得出“圆也是轴对称图形”的结论。这一学习属于（）。

    A.符号学习
    B.并列结合学习
    C.下位学习
    D.上位学习

    答案：C
    解析：
    下位学习是指新知识是原有概念的一个特例或例证，一般有两种情况：(1)新知识纳入原有概念后，新知识获得意义，原有的概念本质不变。(2)新知识纳入原有概念后，不仅使新知识获得意义，而且会扩大、深化原有概念。如，若学生在学习正方形、长方形、三角形时已形成了轴对称图形的概念(已有知识)，在学习圆时，“圆也是轴对称图形”这一命题(新知识)的学习．就是下位学习。在该例中，新学习的内容只是作为已有内容的特例，或只是作为已有内容的证据或例证而加以学习的，因此新学习的内容虽然使已有内容得到了充实或证实，但并未使已有内容发生本质属性的改变；如果将要学习的新内容在包摄和概括水平上高于学习者原有认知结构中已有的相关内容，这时的学习就是上位学习或总括学习。如，学生原有认知结构中已经有了正方形、长方形、三角形的概念，在学习新概念轴对称图形时，发生的就是上位学习。

  • 第2题：

    立方根和平方根的区别与联系?【数学专业问题】


    答案：
    解析：

  • 第3题：

    请列举5个以上常见的轴对称图形，它们的对称轴分别有多少条?【数学专业问题】


    答案：
    解析：
    圆：无数条;等边三角形：3条;菱形：2条;正方形：4条;长方形：2条;正五边形：5条;正六边形：6条。

  • 第4题：

    下列图形中，既是轴对称图形，又是中心对称图形的是（ ）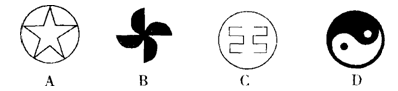


    答案：C
    解析：

  • 第5题：

    三角形衣架是我们日常生活用品，这些衣架都是有两个角相等，这样形成了一个轴对称图形，这个轴对称图形只有一条（）


    正确答案:对称轴

  • 第6题：

    一般将变形问题简化为（）

    • A、平面问题和轴对称问题
    • B、空间问题
    • C、平衡问题
    • D、以上均不对

    正确答案:A

  • 第7题：

    下列关于轴对称问题的叙述，正确的是（）。

    • A、 轴对称应力必然是轴对称位移；
    • B、 轴对称位移必然是轴对称应力；
    • C、 只有轴对称结构，才会导致轴对称应力；
    • D、 对于轴对称位移，最多只有两个边界条件。

    正确答案:B

  • 第8题：

    如果一个图形绕着一个点旋转180°后，能够和原图形完全重合，那么这个图形就叫做（），这个点就是它的对称中心。

    • A、轴对称图形
    • B、中心对称图形
    • C、对称图形

    正确答案:B

  • 第9题：

    单选题
    下列关于轴对称问题的叙述，正确的是（）。
    A

     轴对称应力必然是轴对称位移；

    B

     轴对称位移必然是轴对称应力；

    C

     只有轴对称结构，才会导致轴对称应力；

    D

     对于轴对称位移，最多只有两个边界条件。


    正确答案： D
    解析： 暂无解析

  • 第10题：

    单选题
    学生在学习正方形、长方形、三角形时已形成了轴对称图形的概念（已有知识），在学习圆时，“圆也是轴对称图形”这一命题（新知识）的学习，是（）
    A

    上位学习

    B

    下位学习

    C

    并列学习

    D

    结合学习


    正确答案： B
    解析： 暂无解析

  • 第11题：

    问答题
    一壳体成为回转薄壳轴对称问题的条件是什么？

    正确答案： 1.假设壳体材料连续、均匀、各向同性；受载后变形是小变形；壳壁各层纤维在变形后互不挤压。
    2.所受载荷轴对称。
    3.边界条件轴对称。
    解析： 暂无解析

  • 第12题：

    单选题
    关于对称结构，有如下四种说法，其中正确的是（）。
    A

    只要结构的截面和材料性质对某轴对称就是对称结构

    B

    只要结构的几何形式和支撑情况对某轴对称就是对称结构

    C

    只要结构的几何形式和支撑情况对某轴对称，杆件截面和材料性质也对此轴对称就是对称结构

    D

    只要结构的支撑情况对某轴对称就是对称结构


    正确答案： D
    解析： 暂无解析

  • 第13题：

    下列图形中，是中心对称图形但不是轴对称图形的是（　　）．



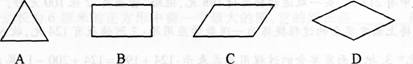    答案：C
    解析：
    平行四边形是中心对称图形，但不是轴对称图形.

  • 第14题：

    初中数学《轴对称现象》
    一、考题回顾
    题目来源1月6日 下午 黑龙江省哈尔滨市 面试考题
    试讲题目1.题目：轴对称现象
    2.内容：
    ?


    3.基本要求：
    (1)有板书设计。
    (2)发现生活中的轴对称图形，体会轴对称图形的含义。
    (3)教学中注意条理清晰，重点突出。
    (4)请在10分钟内完成试讲内容。
    答辩题目1.为什么要学习轴对称现象?
    2.在本节课的教学过程中，你是如何设计探究轴对称现象的?
    二、考题解析
    【教学过程】
    (一)导入新课
    教师描述：同学们，上课之前老师给大家讲一个小故事。(播放动画)在小河边的花丛中，有一只美丽的蝴蝶正在采花蜜。忽然!来了一只蜻蜓在它面前飞来飞去，蝴蝶生气的说“谁在跟我捣乱?”蜻蜓笑嘻嘻地说“你怎么连一家人都不认识了，我是来找你玩的。”这时蝴蝶更生气了，说道：“你是蜻蜓，我是蝴蝶，我们怎么可能是一家人呢?”于是，蜻蜓就落在了旁边的一片叶子上，说：“这你就不知道了吧，不仅蜻蜓、蝴蝶是一家，有些树叶，还有我们身边的很多物体都和我们是一家呢。”故事讲完了，同学们你们明白蜻蜓说的话吗?
    预设：学生们议论纷纷却理解不了蜻蜓话中含义，到这里学生遇到瓶颈，我将顺势引出课题，本节课来学习《轴对称现象》。
    (二)生成新知
    活动一：让学生举出一些生活中轴对称图形的例子，检验学生对于轴对称图形本质特征的认识情况。之后通过大屏幕呈现若干轴对称图形，引导学生去观察，再类比之前所学的内容概括出这些图形的共同特征。
    提问：这些美丽的图形来自生活，认真观察这些图形有什么共同特征?用自己的语言来描述。
    预设：图形左右两部分对称。
    追问：你能将图中的窗花沿某条直线对折，使直线两旁的部分完全重合吗?其他图形呢?
    预设：都能找到一条线使左右完全重合。
    活动二：小组讨论。通过观察，引导学生进行归纳验证，并动手操作“折纸”实验，总结得出轴对称图形和对称轴的相关概念。
    预设：如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是轴对称图形。折痕所在的这条直线叫做对称轴。
    活动三：请大家拿出准备好的图形，动手折一折、画一画，找出它们的对称轴，有几条呢?
    ?


    预设：圆有无数条对称轴，等边三角形有三条对称轴。
    引导学生注意观察自己动手折过的图形以及所画的对称轴，看能不能有什么发现?在同桌交流的基础上，适时引导学生进行归纳总结，得出轴对称的概念：如果一个图形沿着一条直线翻折，能够与另一个图形完全重合，我们称这两个图形关于这条直线成轴对称，这条直线就叫对称轴。
    (三)应用新知
    1.观察下面的图形，哪些图形是轴对称图形?画出对称轴。
    ?


    2.展示活动：自己设计一个优美的轴对称图案。
    (四)小结作业
    小结：通过这节课的学习，你有什么收获?
    作业：找一找语文汉字中哪些字是轴对称图形?
    【板书设计】
    轴对称现象
    轴对称图形：
    对称轴：
    轴对称：
    1.为什么要学习轴对称现象?
    2.在本节课的教学过程中，你是如何设计探究轴对称现象的?


    答案：
    解析：
    1.
    通过学习这一节课，可以让学生对轴对称的知识有一个初步的认识，并为后续学习对称变换、中心对称和中心对称图形及平行四边形的相关知识等做好充分准备。教材通过丰富的现实情境，引导学生关注生活，并自觉加以数学理性上的分析，感受数学的魅力，体会轴对称在生活中的广泛应用，感受数学的美，培养积极的情感、态度、价值观，促进观察、分析、归纳、概括等一般能力和审美意识的发展，为后面研究轴对称的性质和其它数学知识打下基础，在初中数学中占有很重要的位置。
    2.
    在教学过程中，我是根据学生认知的先后顺序，通过观察――讨论――再操作观察――再讨论，一环扣一环的教学。让学生分组讨论，充分参与，自己建立概念，深刻的体验，使学生感受到获得新知的乐趣，从而达到本节课的教学目标。

  • 第15题：

    谈谈你对内容标准中“认识并欣赏自然界和现实生活中的轴对称、中心对称图形，运用图形的轴对称、旋转、平移进行图案设计”要求的认识。


    答案：
    解析：
    数学课程应通过具体内容的设置让学生体会并欣赏到数学的美，认识数学的应用，体会数学的价值；数学课程应通过恰当情境的创设，激发学生对数的好奇心和求知欲，使学生在积极、主动的教学活动中敢于发表自己的想法、勇于质疑，养成认真勤奋、独立思考、合作交流等学习习惯，形成实事求是的科学态度，感受成功的快乐，体验独自客服困难、解决数学问题的过程。内容标准在这些方面作了较好体现，如在图形与几何中“探究勾股定理及其逆定理，并能运用它们解决一些简单的实际问题”‘认识并欣赏自然界和现实生活中的轴对称、中心对称图形”“运用图形的轴对称、旋转、平移进行图案设计…‘通过建筑、艺术上的实例了解黄金分割”等。

  • 第16题：

    若学生在学习正方形、长方形、三角形时已形成了轴对称图形的概念，学习“圆也是轴对称图形”这一新知识，属于哪种概念同化方式？（）

    • A、下位学习
    • B、上位学习
    • C、并列结合学习
    • D、总括性学习

    正确答案:A

  • 第17题：

    学生在学习正方形、长方形、三角形时已形成了轴对称图形的概念（已有知识），在学习圆时，“圆也是轴对称图形”这一命题（新知识）的学习，是（）

    • A、上位学习
    • B、下位学习
    • C、并列学习
    • D、结合学习

    正确答案:B

  • 第18题：

    函数与它的反函数的几何图形关于Y轴对称。


    正确答案:错误

  • 第19题：

    学习正方形中已经掌握的轴对称圆形后，学习时告诉图也是轴对称图形，学生立即发现图具有轴对称特征，这种学习方式是（）

    • A、上位学习
    • B、相关类属
    • C、派生类属
    • D、并列类属

    正确答案:C

  • 第20题：

    单选题
    学习正方形中已经掌握的轴对称圆形后，学习时告诉图也是轴对称图形，学生立即发现图具有轴对称特征，这种学习方式是（）
    A

    上位学习

    B

    相关类属

    C

    派生类属

    D

    并列类属


    正确答案： B
    解析： 派生类属学习，即新学习的知识仅仅是学习者已有概念或命题的一个例证或是一种派生物。例如，学习者掌握了个性心理的基本特征后，就不难理解个性心理中具有代表性的性格的特征了，这种学习不仅使新知识获得了意义，而且使原有知识获得了证实或扩充。

  • 第21题：

    单选题
    若学生在学习正方形、长方形、三角形时已成形轴对称图形概念，在学习圆时，“圆也是轴对称图形”这一命题被纳入或类属于原有轴对称图形概念，新的命题很快就获得意义，学生立即能发现圆具有轴对称图形的一切特征这种概念学习的形式是（）
    A

    相关类属过程

    B

    派生类属学习

    C

    上位学习

    D

    并列结合学习


    正确答案： B
    解析： 暂无解析

  • 第22题：

    单选题
    若学生在学习正方形、长方形、三角形时已形成了轴对称图形的概念，学习“圆也是轴对称图形”这一新知识，属于哪种概念同化方式？（）
    A

    下位学习

    B

    上位学习

    C

    并列结合学习

    D

    总括性学习


    正确答案： A
    解析： 暂无解析

  • 第23题：

    单选题
    一般将变形问题简化为（）
    A

    平面问题和轴对称问题

    B

    空间问题

    C

    平衡问题

    D

    以上均不对


    正确答案： B
    解析： 暂无解析

相关内容