计算s=1+3+5+7+9的算法流程如图8所示,若要计算s=2×3×5×7×9,则下面流程图中的
题目


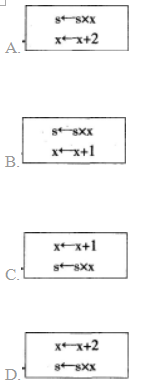
相似考题
更多“计算s=1+3+5+7+9的算法流程如图8所示,若要计算s=2×3×5×7×9,则下面流程图中的 ”相关问题
-
第1题:
下面程序段是计算()公式的。s=0:t=1Fori=1To10t=t*is=s+tNexti
A.s=1+2+3+4+5+6+7+8+9+10
B.s=1*2*3*4*5*6*7*8*9*10
C.s=1!+2!+3!+4!+5!+6!+7!+8!+9!+10!
D.s=1+2*3+3*4+4*5+5*6+6*7+7*8+8*9+9*10
正确答案:C
-
第2题:
阅读下列说明和流程图,将应填入(n)的字句写在对应栏内。
【说明】
下列流程图(如图4所示)用泰勒(Taylor)展开式
sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x2n+1/(2n+1)!+…
【流程图】
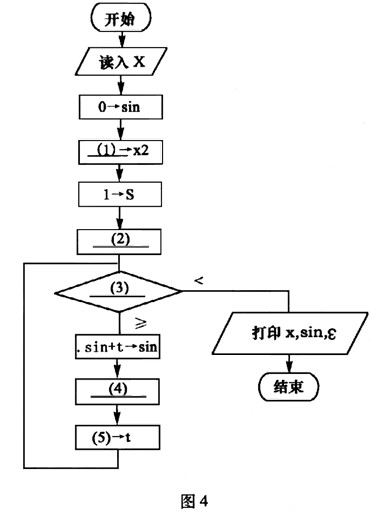
计算并打印sinx的近似值。其中用ε(>0)表示误差要求。
正确答案:(1)x*x (2)x->t (3)│t│:ε (4)s+2->s (5)(-1) * t* x2/(s* (s-1))
(1)x*x (2)x->t (3)│t│:ε (4)s+2->s (5)(-1) * t* x2/(s* (s-1)) 解析:该题的关键是搞清楚几个变量的含义。很显然变量t是用来保存多项式各项的值,变量s和变量x2的作用是什么呢?从流程图的功能上看,需要计算11、3!、5!,……,又从变量s的初值置为1可知,变量s主要用来计算这此数的阶乘的,但没有其他变量用于整数自增,这样就以判断s用来存储奇数的,即s值依次为1、3、5,……。但x2的功能还不明确,现在可以不用管它。
(2)空的作用是给t赋初值,即给它多项式的第一项,因此应填写“x->t”。(3)空处需填写循环条件,显然当t的绝对值小于ε(>0)就表示已经达到误差要求,因此(3)空应填入“│t│:ε”。由变量s的功能可知,(4)空应当实现变量s的增加,因此(4)空应填入“s+2->s”。 (5)空应当是求多项式下一项的值,根据多项式连续两项的关系可知,当前一项为t时,后一项的值为(-1)*t*x*x/(s*(s-1))。但这样的话,每次循环都需要计算一次x*x,计算效率受到影响,联想到变量x2还没用,这时就可以判断x2就是用来存储x*x的值,使得每次循环者少进行一次乘法运算。因此(1)空处应填入“x*x”,(5)空处应填入“(-1)*t*x2/(s*(s-1))”。 -
第3题:
阅读以下程序: includevoid main() { static int a[][3]={9,7,5,3,1,2,4,6,8}; int 阅读以下程序:
include<iostream.h>
void main()
{
static int a[][3]={9,7,5,3,1,2,4,6,8};
int i,j,s1=0,s2=0;
for(i=0;i<3;i++)
for(j=0;j<3;j++)
{
if(i==j)s1=sl+a[i][j];
if(i+j==2)s2=s2+a[i][j];
}
cout<<s1<<","<<s2<<endl;
}
则该程序的输出结果为【 】。
正确答案:1810
18,10 -
第4题:
若按下式计算奇校验位,则上述流程图中的(1)处应填(5)。
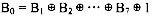 正确答案:(5)1
正确答案:(5)1
(5)1 -
第5题:
若有如下程序: sub(p,n) int(*p)[3],n; { int i; for(i=0;i<=n;i++) printf("%d",*(*(p+i)+n)); } main() {int s[3][3]={1,2,3,4,5,6,7,8,9}; sub(s,2); } 则程序运行后的输出结果是( )
A.3 6 9
B.2 4 8
C.4 5 6
D.7 8 9
正确答案:A
-
第6题:
阅读以下说明和流程图,回答问题1和问题2。
【说明】
为便于管理,每本正式出版的图书都印有国际标准书号。标准书号由“ISBN”和 10个数字组成,其格式为:ISBN组号-出版者号-书名号-校验码。其中,校验码是根据前面9个数字计算得到的,用于计算机自动校验。假设标准书号的10个数字依次是 a(1),a(2),…,a(10),则校验码a(10)的设置应使S=10*a(1)+9*a(2)+8*a(3)+…1*a(10)能被 11整除。如果校验码a(10)应设置成10,则规定以“X”表示之。例如,信息处理技术员纲的标准书号为:ISBN 7-302-11191-X。第1段上的数字“7”是国际ISBN中心分配给中国ISBN中心管理的组号。第2段上的“302”表示清华大学出版社。标准书号的校验过程如图1-1所示,计算校验码的过程如图1-2所示,其中,Mod(S,11)表示S除以11得到的余数。
【流程图】
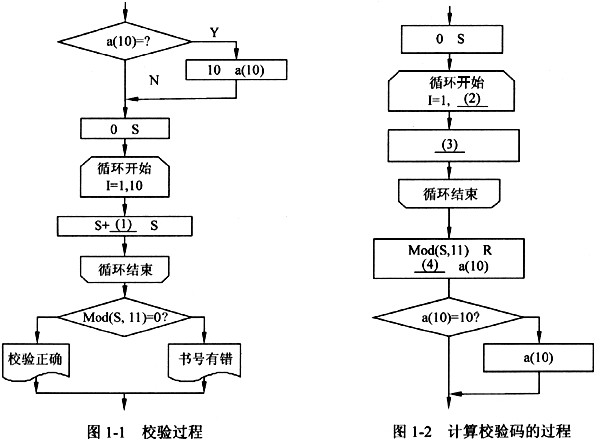
请填补流程图中的空缺(1)~(4)。
正确答案:(1)(11-I)*a[I](或I*a(11-I)) (2)9 (3)S+(11-I)*a[I]→S(或S+(I+1)*a(10-I)→S) (4)MOD(11-R11)
(1)(11-I)*a[I](或I*a(11-I)) (2)9 (3)S+(11-I)*a[I]→S(或S+(I+1)*a(10-I)→S) (4)MOD(11-R,11) -
第7题:
若采用白盒测试法对下面流程图所示算法进行测试,且要满足语句覆盖,则至少需要(51)个测试用例,若表示输入和输出的测试用例格式为(A,B,X;X),则满足语句覆盖的测试用例是(52)。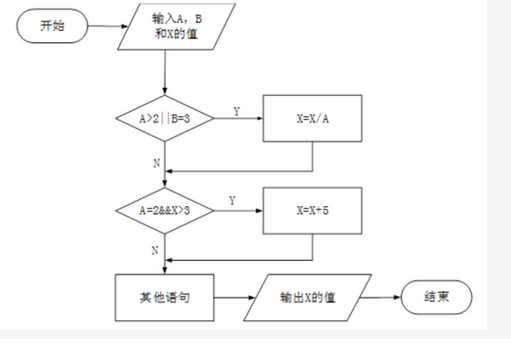 A. (1,3,3;8)
A. (1,3,3;8)
B. (1,3,5;10)
C. (5,2,15;8)
D. (5,2,20;9)答案:A解析:白盒测试方法: (1)语句覆盖。被测程序的每个语句至少执行一次。是一种很弱的覆盖标准。 (2)判定覆盖。也称为分支覆盖,判定表达式至少获得一次真、假值。判定覆盖比语句覆盖强。 (3)条件覆盖。每个逻辑条件的各种可能的值都满足一次。 (4)路径覆盖。覆盖所有可能的路径。 (5)判定/条件覆盖。每个条件所以可能的值(真/假)至少出现一次。 (6)条件组合覆盖。每个条件的各种可能值的组合都至少出现一次。 此处只需要一个测试用例就可以完成所有的语句覆盖。 此题有误,无正确答案。按照要求,应该选择A=2.B=3,X取任意值。 -
第8题:
如图4所示的流程图,若输入的值是-5时,输出的结果为( )。
 A.-9
A.-9
B.-3
C.O
D.3答案:D解析:①A=-5,小于0,则A=-5+2,A=-3;
②A=-3,小于0,则 A=-3+2,A=-1;
③A=-1,小于0,则A=-1+2,A=1;
④A=1,不小于0,则A=1×3,A=3。 -
第9题:
计算s=1+3+5+7+9的算法流程如图8所示,若要计算s=1×3×5×7×9,则下面流程图中的
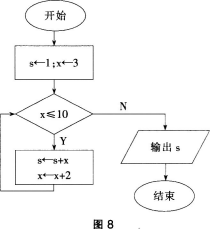
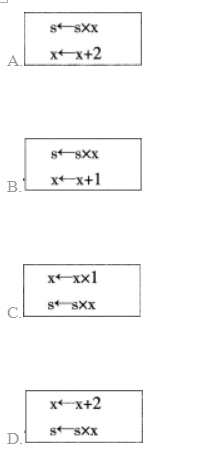 答案:A解析:题中将s=1+3+5+7+9,改成计算s=1×3×5×7×9,变量x的步长还是2,所以应该修改为s←s×x,x←x+2。
答案:A解析:题中将s=1+3+5+7+9,改成计算s=1×3×5×7×9,变量x的步长还是2,所以应该修改为s←s×x,x←x+2。 -
第10题:
如图7所示的流程图功能是将键盘输入的非0数进行累加.当输入的数为0时则输出它们的和。则图中虚线部分的内容是( )。
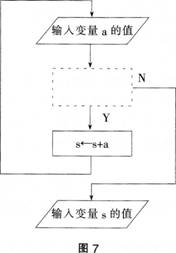
 答案:B解析:本题的功能是让键盘输入的非0数进行累加,当输入的数为0时则输出它们的和。判断的条件用菱形表示。故选择B选项。
答案:B解析:本题的功能是让键盘输入的非0数进行累加,当输入的数为0时则输出它们的和。判断的条件用菱形表示。故选择B选项。 -
第11题:
某算法的流程图如下所示: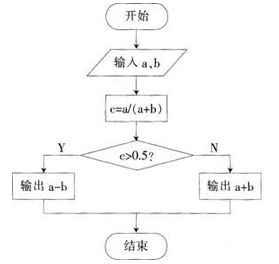
当输入a的值为5,b的值为7时,该算法的输出结果为( )。A.2
B.5
C.7
D.12答案:D解析:【知识点】算法
【答案】D。
【解析】c=5/(5+7)≈0.47<0.5,所以进入右侧的分支,输出的是a+b=12。 -
第12题:
下面是一段关于计算变量s的算法: ①变量s的初值是0 ②变量i从1起循环到n,此时变量s的值由下面的式子表达式计算 ③s=s+(-1)*i ④输出变量s的值 这个计算s值的算法中,s的代数式表示是()。
- A、1-2+3-4+…+(-1)n*(n-1)
- B、1-2+3-4+…+(-1)n-1*n
- C、1+2+3+4+...+(n-1)+n
- D、-1-2-3-4-...-n
正确答案:D -
第13题:
阅读以下说明和流程图,回答问题1~2,将解答填入对应的解答栏内。
[说明]
下面的流程图描述了计算自然数1到N(N≥1)之和的过程。
[流程图]
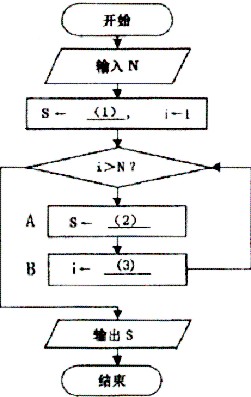
[问题1] 将流程图中的(1)~(3)处补充完整。
[问题2] 为使流程图能计算并输出1*3+2*4+…+N*(N+2)的值,A框内应填写(4);为使流程图能计算并输出不大于N的全体奇数之和,B框内应填写(5)。
正确答案:(1) 0 (2) S+i (3) i+1 (4) S←S+i*(i+2) (5) i←i+2
(1) 0 (2) S+i (3) i+1 (4) S←S+i*(i+2) (5) i←i+2 解析:本题中,变量i用作循环变量,变量S则用于存放累加和,起初始值为0。在计算1+2+…+N时,每循环一次,将i的值累加到当前的S中,并且i自增1。为计算1*3+2*4+…+N*(N+2)的值,只需将其第i项的值i*(i+2)累加到S中;为计算不大于N的全体奇数之和,令循环变量的步长为2即可。 -
第14题:
阅读以下说明和流程图,填补流程图中的空缺(1)一(5),将解答填入答题纸的对应栏内。
【说明】
下面的流程图采用公式ex=1+x+x2/2 1+x3/3 1+x4/4 1+…+xn/n!+???计算ex的近似值。设x位于区间(0,1),该流程图的算法要点是逐步累积计算每项xx/n!的值(作为T),再逐步累加T值得到所需的结果s。当T值小于10-5时,结束计算。
【流程图】
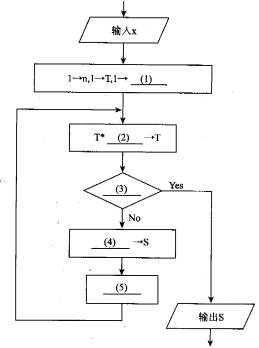 正确答案:(1)S (2)x/n (3)T<O.00001 (4)S+T (5)n+1->n
正确答案:(1)S (2)x/n (3)T<O.00001 (4)S+T (5)n+1->n
(1)S (2)x/n (3)T<O.00001 (4)S+T (5)n+1->n 解析:在题目中已经给出了指数函数ex的公式,即基本算法,另外也给出了计算过程中控制误差终止计算的方法。本题主要的重点是如何设计计算流程,实现级数前若干项的求和,以及判断计算终止的条件。级数求和一般都是采用逐项累加的方法。从流程图我们可以看出s为累加结果,T为动态的项值,最后通过s+T->S来完成各项的累加。已知T=xnx/n!,如果每次都直接计算T的值,计算量会比较大。从ex的公式中我们可以看出每一项都一个共同点,就是后一项和前一项有简单的关系Tn=T(n-i)*x/n,我们可以充分利用前项的计算结果来计算后一项,这样就会大大减少计算量。这也是程序员需要掌握的基本技巧。在流程图中,一开始先输入变量x,接着对其他变量赋初值。级数项号n的初始值为1,逐次进行累积的T的初始值为1,根据后面的流程推断可以看出逐次进行累加的s应该有初始值l的(在输入的x满足条件直接退出循环的时候根据公式输出的值为D,所以空(1)的答案为“S”。从前面分析直到e。的公式中后一项和前一项有简单的关系Tn=T(n-i)*x/n,所以空(2)的答案为“x/n”。空(3)处是判断计算过程结束的条件,按照题目中的要求“当T值小于lO-5时,结束计算。”所以空(3)的答案为“T<0.00001”。按照题意空(4)处是要对每项的结果进行累加赋给S,实现s+T->s,所以空(4)的答案为“S+T”。流程走到空(5)的时候已经求出第n项的值Tn,并累加到s中,根据算法下一步应该计算第n+1项的值,所以这里需要对级数的项号n进行自增,空(5)的答案可以为“n+=1”或者n++,但是根据流程图以上的书写风格写为“n+1->n”应该是最佳答案。 -
第15题:
阅读以下标准书号校验码的技术说明和程序流程图,根据要求回答问题1至问题3。
[说明]
为实现图书的国际统一编码,便于实现计算机化的图书管理,每本正式出版的图书都印有国际标准书号。标准书号由“ISBN”、10个数字(0~9)组成,其格式如下。
ISBN 组号-出版者号-书名号-校验码
其中,校验码是根据前面9个数字计算得到的,用于计算机自动校验。假设标准书号的10个数字依次是a(1),a(2),…,a(10),则校验码a(10)的设置应使S=10*a(1)+9*a(2)+8*a(3)+…+1*a (10)能被11整除。如果校验码a(10)应设置成10,则规定以“X”表示之。
例如,《软件设计师考试考前冲刺预测卷及考点解析》的标准书号为:ISBN7-121-05027-5。第1段上的数字“7”是国际ISBN中心分配给中国ISBN中心管理的组号;第2段上的“121”表示电子工业出版社。标准书号的校验过程如图5-13所示,计算校验码的过程如图5-14所示。其中,Mod(S,11)表示S除以11得到的余数。

请根据标准书号校验码的技术说明,将图5-13和图5-14程序流程图中(1)~(4)空缺处的内容填补完整。
正确答案:制订标准书号的目的是实现图书的国际统一编码以便于实现计算机化的图书管理使出版社内的图书管理、书库中的图书管理以及书店的图书销售管理具有更高的工作效率和管理水平。标准书号由“ISBN”、10个数字(0~9)组成采用“ISBN 组号-出版者号-书名号-校验码”的格式。其中出版者号规定为2-7位数字。对较大的出版社分配比较短的码留出较长的书名号为较多的书进行编码。 标准书号的最后一位是校验码。设置校验码可以大大减少录入错误造成的管理混乱。校验码一般由计算机程序产生。当操作人员录入前9个数字后计算机就会自动启动计算校验码的过程输出正确的校验码。在书店(或书库)不论是建库还是查询检索在手工输入带校验码的标准书号后计算机就会自动启动校验过程判断是否输入错误。 在图5-14计算校验码的过程中首先要计算部分S值即S=10*a(1)+9*a(2)+8*a(3)+…+2*a (9)。此时需要使用循环处理。在循环开始之前应设置初始值S=0。在循环体内应执行语句“S+=(11-I) *a(I)”或“S+=(1+I)*a(10-I)”(注意其中的乘号“*”不要丢失)。该循环应对循环变量I=1~9进行(步长默认为1)控制因此(2)空缺处应填入“9”(3)空缺处所填写的内容是“S+(11-I)*a[I]->S”或“S+(1+I)*a(10-I)->S”。 接着再计算该S值除以11的余数R。显然 。由于“校验码a(10)的设置应使S=10*a(1) +9*a(2)+8*a(3)+…+1*a(10)能被11整除”即余数R与校验码之和应能被11整除因此校验码应等于MOD(11-R 11)即(4)空缺处所填写的内容是“MOD(11-R 11)”。若读者该空缺处填入“MOD (11-R)”则是没有考虑R=0这一情况。当校验码等于10时还应以符号X表示之。
在对标准书号的校验过程(图5-13)中首先要将校验码为X的情况转换成数据10以便于后续计算。为了计算S=10*a(1)+9*a(2)+8*a(3)+…+1*a(10)需要使用循环处理。在循环开始之前应0设置初始值S=0对循环变量I从1到10(步长默认为1)。在循环体内应执行语句“S+=(11-I)*a(I)”或“S+=I*a(11-I)”。因此(1)空缺处所填写的内容是“(11-I)*a(I)”或“I*a(11-I)”。
在图5-13中计算出S值之后还应判断S除以11的余数是否为0。若余数为0说明S能够被11整除表示校验结果正确;若余数非0则说明输入的标准书号有错(可能是校验码输入有错也可能是前面的数字输入有错)。此时计算机应输出相应的错误提示信息提醒信息录入人员仔细校对改正。
。由于“校验码a(10)的设置应使S=10*a(1) +9*a(2)+8*a(3)+…+1*a(10)能被11整除”即余数R与校验码之和应能被11整除因此校验码应等于MOD(11-R 11)即(4)空缺处所填写的内容是“MOD(11-R 11)”。若读者该空缺处填入“MOD (11-R)”则是没有考虑R=0这一情况。当校验码等于10时还应以符号X表示之。
在对标准书号的校验过程(图5-13)中首先要将校验码为X的情况转换成数据10以便于后续计算。为了计算S=10*a(1)+9*a(2)+8*a(3)+…+1*a(10)需要使用循环处理。在循环开始之前应0设置初始值S=0对循环变量I从1到10(步长默认为1)。在循环体内应执行语句“S+=(11-I)*a(I)”或“S+=I*a(11-I)”。因此(1)空缺处所填写的内容是“(11-I)*a(I)”或“I*a(11-I)”。
在图5-13中计算出S值之后还应判断S除以11的余数是否为0。若余数为0说明S能够被11整除表示校验结果正确;若余数非0则说明输入的标准书号有错(可能是校验码输入有错也可能是前面的数字输入有错)。此时计算机应输出相应的错误提示信息提醒信息录入人员仔细校对改正。
制订标准书号的目的是实现图书的国际统一编码,以便于实现计算机化的图书管理,使出版社内的图书管理、书库中的图书管理以及书店的图书销售管理具有更高的工作效率和管理水平。标准书号由“ISBN”、10个数字(0~9)组成,采用“ISBN 组号-出版者号-书名号-校验码”的格式。其中,出版者号规定为2-7位数字。对较大的出版社分配比较短的码,留出较长的书名号为较多的书进行编码。 标准书号的最后一位是校验码。设置校验码可以大大减少录入错误造成的管理混乱。校验码一般由计算机程序产生。当操作人员录入前9个数字后,计算机就会自动启动计算校验码的过程,输出正确的校验码。在书店(或书库),不论是建库还是查询检索,在手工输入带校验码的标准书号后,计算机就会自动启动校验过程,判断是否输入错误。 在图5-14计算校验码的过程中,首先要计算部分S值,即S=10*a(1)+9*a(2)+8*a(3)+…+2*a (9)。此时需要使用循环处理。在循环开始之前,应设置初始值S=0。在循环体内,应执行语句“S+=(11-I) *a(I)”或“S+=(1+I)*a(10-I)”(注意,其中的乘号“*”不要丢失)。该循环应对循环变量I=1~9进行(步长默认为1)控制,因此,(2)空缺处应填入“9”,(3)空缺处所填写的内容是“S+(11-I)*a[I]->S”或“S+(1+I)*a(10-I)->S”。 接着再计算该S值除以11的余数R。显然 。由于“校验码a(10)的设置应使S=10*a(1) +9*a(2)+8*a(3)+…+1*a(10)能被11整除”,即余数R与校验码之和应能被11整除,因此校验码应等于MOD(11-R, 11),即(4)空缺处所填写的内容是“MOD(11-R, 11)”。若读者该空缺处填入“MOD (11-R)”,则是没有考虑R=0这一情况。当校验码等于10时,还应以符号X表示之。
在对标准书号的校验过程(图5-13)中,首先要将校验码为X的情况转换成数据10,以便于后续计算。为了计算S=10*a(1)+9*a(2)+8*a(3)+…+1*a(10),需要使用循环处理。在循环开始之前,应0设置初始值S=0,对循环变量I从1到10(步长默认为1)。在循环体内,应执行语句“S+=(11-I)*a(I)”或“S+=I*a(11-I)”。因此(1)空缺处所填写的内容是“(11-I)*a(I)”或“I*a(11-I)”。
在图5-13中,计算出S值之后,还应判断S除以11的余数是否为0。若余数为0,说明S能够被11整除,表示校验结果正确;若余数非0,则说明输入的标准书号有错(可能是校验码输入有错,也可能是前面的数字输入有错)。此时计算机应输出相应的错误提示信息,提醒信息录入人员仔细校对改正。
。由于“校验码a(10)的设置应使S=10*a(1) +9*a(2)+8*a(3)+…+1*a(10)能被11整除”,即余数R与校验码之和应能被11整除,因此校验码应等于MOD(11-R, 11),即(4)空缺处所填写的内容是“MOD(11-R, 11)”。若读者该空缺处填入“MOD (11-R)”,则是没有考虑R=0这一情况。当校验码等于10时,还应以符号X表示之。
在对标准书号的校验过程(图5-13)中,首先要将校验码为X的情况转换成数据10,以便于后续计算。为了计算S=10*a(1)+9*a(2)+8*a(3)+…+1*a(10),需要使用循环处理。在循环开始之前,应0设置初始值S=0,对循环变量I从1到10(步长默认为1)。在循环体内,应执行语句“S+=(11-I)*a(I)”或“S+=I*a(11-I)”。因此(1)空缺处所填写的内容是“(11-I)*a(I)”或“I*a(11-I)”。
在图5-13中,计算出S值之后,还应判断S除以11的余数是否为0。若余数为0,说明S能够被11整除,表示校验结果正确;若余数非0,则说明输入的标准书号有错(可能是校验码输入有错,也可能是前面的数字输入有错)。此时计算机应输出相应的错误提示信息,提醒信息录入人员仔细校对改正。
-
第16题:
对于如图7-5所示的程序流程图中,当采用语句覆盖法设计测试案例时,至少需要设计(36)个测试案例。

A.3
B.4
C.2
D.1
正确答案:D
解析:语句覆盖是一种设计测试案例的方法,它要求对于设计的测试案例,必须使得程序的每一条可执行语句至少执行一次。对于图7-5所示的程序流程图可设计如下测试案例。
案例1:X=1,Y=2
此时执行语句序列为:X>0→Y=Y-X→Y>0→X=1。
案例2:X=-3,Y=2
此时执行语句序列为:X>0→Y=Y+X→Y>0→X=-1。
可见,只需设计两个测试案例即可使得程序的每条可执行语句至少执行一次。 -
第17题:
●试题一
阅读下列说明和流程图,将应填入(n)的字句写在答题纸的对应栏内。
【说明】
下列流程图(如图4所示)用泰勒(Taylor)展开式
sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x 2n+1/(2n+1)!+…
【流程图】
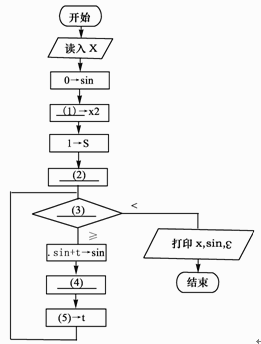
图4
计算并打印sinx的近似值。其中用ε(>0)表示误差要求。
正确答案:
●试题一【答案】(1)x*x(2)x->t(3)|t|∶ε(4)s+2->s(5)(-1)*t*x2/(s*(s-1))【解析】该题的关键是搞清楚几个变量的含义。很显然变量t是用来保存多项式各项的值,变量s和变量x2的作用是什么呢?从流程图的功能上看,需要计算1!、3!、5!,……,又从变量s的初值置为1可知,变量s主要用来计算这此数的阶乘的,但没有其他变量用于整数自增,这样就以判断s用来存储奇数的,即s值依次为1、3、5,……。但x2的功能还不明确,现在可以不用管它。(2)空的作用是给t赋初值,即给它多项式的第一项,因此应填写"x->t"。(3)空处需填写循环条件,显然当t的绝对值小于ε(>0)就表示已经达到误差要求,因此(3)空应填入"|t|∶ε"。由变量s的功能可知,(4)空应当实现变量s的增加,因此(4)空应填入"s+2->s"。(5)空应当是求多项式下一项的值,根据多项式连续两项的关系可知,当前一项为t时,后一项的值为(-1)*t*x*x/(s*(s-1))。但这样的话,每次循环都需要计算一次x*x,计算效率受到影响,联想到变量x2还没用,这时就可以判断x2就是用来存储x*x的值,使得每次循环者少进行一次乘法运算。因此(1)空处应填入"x*x",(5)空处应填入"(-1)*t*x2/(s*(s-1))"。 -
第18题:
计算题:如图1所示的程序流程图,试计算其巡回秩数V(G)。

由程序流程图画流图或称程序图如图2所示。于是有:
(1)V(G)=E–N+2=13–10+2=5
(2)V(G)=封闭区域个数=5
(3)V(G)=谓词结点个数+1=P+1=4+1=5 -
第19题:
阅读说明和流程图,填补流程图中的空缺(1)?(5),将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1,a2=1,…,an=an-1+an-2!n=3,4,…}的前n项(n>=2) 之和S。例如,菲波那契数列前6项之和为20。计算过程中,当前项之前的两项分别动态地保存在变量A和B中。【流程图】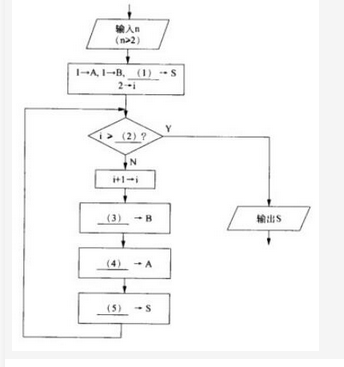 答案:解析:(1)2或A+B(2)n(3)A+B(4)B-A(5)S+B
答案:解析:(1)2或A+B(2)n(3)A+B(4)B-A(5)S+B
【解析】
菲波那契数列的特点是首2项都是1,从第3项开始,每一项都是前两项之和。该数列的前几项为1,1,2, 3,5,8,…。在流程图中,送初始值1—A,2—B后,显然前2项的和S应等于2,所以(1)处应填2 (或A+B)。此时2→i (i表示动态的项编号),说明已经计算出前2项之和。接着判断循环的结束条件。显然当i=n时表示已经计算出前n项之和,循环可以结束了。因此(2)处填n。判断框中用“>”或“≥”的效果是一样的,因为随着i的逐步增1,只要有i=n结束条件就不会遇到i>n的情况。不过编程的习惯使循环结束条件扩大些,以防止逻辑出错时继续循环。接下来i+1→i表示数列当前项的编号增1,继续往下计算。原来的前两项值(分别在变量A和B中)将变更成新的前两项再放到变量A和B中。
首先可以用A+B—B实现(原A) + (原B)—(新B),因此(3)处填A+B。为了填新A值(原来的B值),不能用B—A,因为变量B的内容已经改变为(原A) + (原B),而B-A正是((原A) + (原B))-(原A)=(原B),因此可以用B-A—A来实现新A的赋值。这样,(4)处填B-A。最后应是前n项和值的累加(比原来的S值增加了新B值),所以(5)处应填S+B。填完各个空后,最好再用具体的数值来模拟流程图走几个循环检查所填的结果(这是防止逻辑上出错的好办法)。 -
第20题:
某算法的流程图如下所示:
当输人a、b的值分别为7、9,该算法的输出结果为( )。A.16
B.9
C.7
D.2答案:A解析:【知识点】算法
【答案】A。
【解析】输入a和b以后进行判断,7不大于9,所以进入右边分支c=a+b,所以最后输出的c=7+9=16。 -
第21题:
计算s=1+1/3+1/7+1/15+……的流程图如图10所示,若要计算前5项的和,①处应该输入的判断条件是()。
A.n<6
B.n<=5
C.n<4
D.n<=4答案:D解析:题干当中求的是前5项的和,那么n的取值是0,1,2,3,4。 -
第22题:
某计算公式的流程图如图5所示。输出结果s的值为()。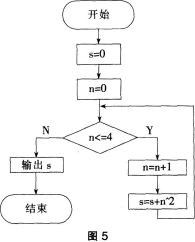
A.14
B.30
C.55
D.91答案:C解析:判断框中的判断条件为n<=4,当判断框中n=4时,依然执行右边,n=n+1:4+1=5,s=s+n^2=0+1^2+2^2+3^2+4^2+5^2=55。当n=5时,不满足判断框中的条件,所以流程图转向左边,输出s的数值为55。 -
第23题:
如图2所示的算法流程图,当输入值为2时,其输出结果是()。
A.2
B.3
C.4
D.5答案:B解析:输入2时,x=2>0,所以进入左边的分支,y=2x-1=3,所以输出的是3。
